Вопрос 11. Модели, построенные с использованием эргодических Марковских цепей.

Марковский процесс называется эргодическим (возвратным), если из любого состояния в любое другое состояние можно перейти за конечное число шагов. Эргодический Марковский процесс никогда не завершается, а постоянно переходит из одного состояния в другое с различной частотой, зависящей от вероятностей переходов. Эргодическая Марковская цепь описывает установившиеся процессы в системе. Характерной особенностью этой цепи является то, что вероятности пребывания системы в каком-то состоянии не зависит от времени и численно равно математическому ожиданию доли времени пребывания системы в этом состоянии. Поэтому уравнения А.Н. Колмогорова превращаются в алгебраические.

Эргодические Марковские цепи широко используются для составления моделей надёжности систем, а также в качестве математического аппарата для расчёта других более сложных моделей (см. ниже).

Рассмотрим применение поглощающей Марковской цепи на конкретном примере. Граф, моделирующий надёжность дублированной системы, работающей в установившемся режиме с постоянно включенным резервом и обслуживанием.

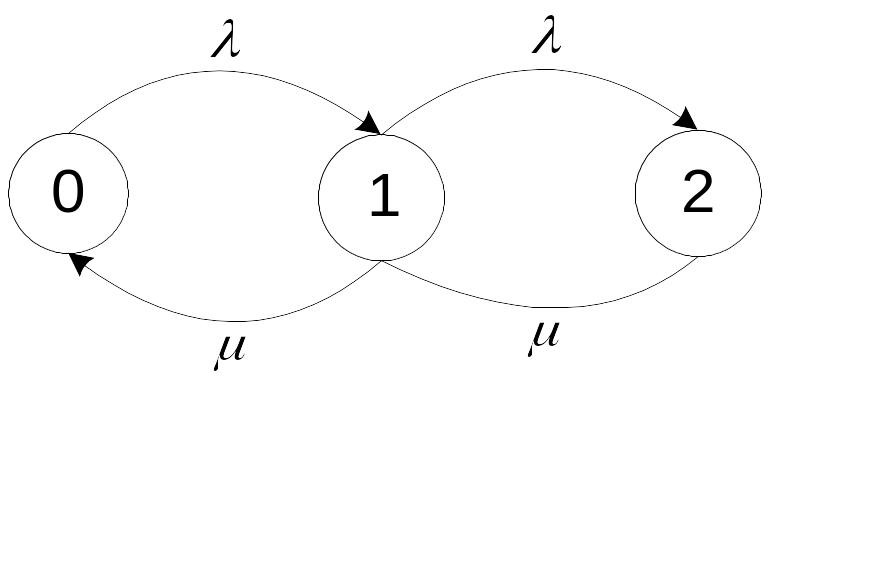
Если составить уравнения для всех трёх состояний, то получится система связанных между собой уравнений (любое из этих уравнений можно получить путём комбинации остальных двух). Для получения независимых уравнений составим их для любых двух состояний, например для первого и второго. Третье уравнение – сумма вероятностей нахождения системы во всех состояниях равна единице.

-P₀  + P₁  = 0;

Р₀-()Р₁+Р₂=0;

-P₂  + P₁  = 0.

Р₀+ Р₁+ Р₂ = 1.

Коэффициент готовности системы равен: K_Г = Р₀ + Р₁.

Вопрос 12.

Использование теории распознавания образов в моделировании.

Распознавание образов представляет собой процесс принятия решения, устанавливающего принадлежность распознаваемого объекта к некоторому классу, путём сравнения его характеристик с характеристиками ранее изученных объектов.

Основными понятиями теории распознавания образов являются: объект, признак, класс, решающее правило, решающая функция, обучающая последовательность объектов.

Объект – предмет или явление, исследуемое в конкретной задаче. Каждый объект характеризуется некоторым набором параметров или свойств. Параметры, с помощью которых любой объект можно отличить от другого объекта, называются признаками. Таким образом, каждый объект можно описать с помощью некоторого набора признаков x_1, x₂,…,x_n,которые образуют вектор признаков объекта X=(x_1, x₂, …,x_n).

Признаки делятся на количественные и качественные:

Чаще всего эти признаки центрируют:

Классом называется совокупность объектов, обладающих некоторыми общими признаками.

Решающее правило – алгоритм, позволяющий по совокупности признаков отнести объект к тому или другому классу.

Решающая функция – аналитическое уравнение, принимающее максимальное значение при подстановке в него признаков объекта данного класса.

Обучающая последовательность – выборка объектов с указанием их признаков и принадлежности к классам.

Типы задач, решаемых с применением методов теории распознавания объектов:

• автоматическая классификация объектов;

• выбор наиболее информативных признаков;

• распознавание объектов (определение того, к какому классу они относятся);

• прогнозирование значений отдельных параметров по косвенным признакам (в случаях, когда непосредственное измерение параметров затруднено);

• техническая диагностика видов неисправностей и пр.

Последние три задачи используют одни и те же методы, а именно, метод распознавания объектов.

Все алгоритмы построения решающего правила разделяются на две группы: детерминистические и вероятностные. Особенность детерминистических – классы чётко разделяются друг от друга и не пересекаются, а объект с какими-либо признаками с вероятностью 1 относится к какому-то классу.