Вопрос 7. Нахождение коэффициентов регрессионного уравнения.

Точное значение коэффициентов b_i регрессионного уравнения возможно только при бесконечно большом объёме выборки. Поэтому при ограниченном объёме выборки определяют оценки этих коэффициентов _i. Исследуемое выражение будет иметь следующий вид:

где β_i – оценка математического ожидания, х₁=1.

_I – находим по выборке, используя метод наименьших квадратов.

Функция наименьших квадратов имеет следующий вид:

где _j – экспериментальное значение выходной величины в j-том эксперименте, x_ij – значение i-той входной переменной в в j-том эксперименте. m – число слагаемых, N – Число эспериментов.

Нужно найти минимум I, тогда найдём коэфф.

В данном выражении неизвестными являются коэффициенты _i. Рассматривая эти коэффициенты как независимые переменные, и приравняв к нулю частные производные от I по _i , получим m уравнений с m неизвестными, решив которые и найдём эти коэффициенты.

Пример 1. Определим зависимость основного удельного сопротивления движению отцепа от температуры. Результаты эксперимента с наиболее лёгким отцепом (22 тонны).

Удельное сопротивление движению wo	Температура наружного воздуха, оС
	Выше 0	-5	-15	-25	-35
	2,56	4,20	3,58	4,27	4,33

Пусть регрессионное уравнение имеет вид: w_o=₁+₂t+₃t².

В результате дифференцирования этого уравнения по _i получим три линейных уравнения, решив которые и найдём искомые коэффициенты.

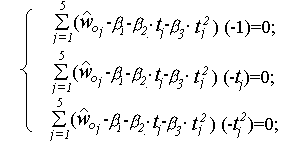
Решив эту систему уравнений, получим следующую зависимость удельного сопротивления движения отцепа от температуры:

w_o(t)= 3.133 - 0,061 t – 7.3510^-4 t²

Удельное сопротивление движению wo	Температура наружного воздуха
	Выше 0	-5	-15	-25	-35
	3.133	3.417	3.91	4.199	4.368

Вопрос 8. Выбор типа регрессионного уравнения

Как слишком упрощенные, так и слишком усложнённые модели являются неточными.

Для построения подходящей регрессионной модели рекомендуется использовать метод пошаговой регрессии. Разработчик априорно намечает перечень входных переменных k и составляет k уравнений вида y=₁+₂x_i, i=1..k.

Методом наименьших квадратов для каждого уравнения определяют оценки параметров ₁ и ₂. и среднеквадратичные отклонения I.

Среднеквадратичное отклонение вычислялось по формуле:

По минимуму среднеквадратичного отклонения выбирают наиболее информативный фактор (обозначим его буквой m). Затем составляют k-1 уравнений вида y=₁+_mx_m+_Ix_i, i=1..k, im.

Определяют оценки параметров уравнения  и по минимуму среднеквадратичного отклонения определяют следующий фактор и т.д. Процесс повторяют до тех пор, пока полученная модель не будет иметь достаточную точность, о которой можно судить по величине среднеквадратичной ошибки.

Потом добавляются остальные факторы, в качестве произведения, и так, и опять считают всё снова.

Проверка значимости регрессионного уравнения.

После очередного включения следующего слагаемого в регрессионное уравнение необходимо проверить значимость полученного уравнения. Для этого можно использовать различные критерии, например, Пирсона, Стьюдента, Колмогоров. Но чаще всего при определении значимости регрессионного уравнения используют критерий Фишера. Уравнение считается значимым, если соблюдается следующее неравенство:

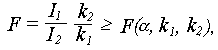
где I₁ – суммарное квадратичное отклонение, учитываемое уравнением;

I₂ – суммарное квадратичное отклонение, не учитываемое уравнением;

k₁ , k₂ – степени свободы;

k₁=m, k₂ =N – m – 1;

N – количество экспериментов;

m – число учтённых в модели факторов.

Число не учитываемых уравнением квадратов отклонений определяется по формуле:

Для подсчёта числа квадратов отклонений, учитываемых уравнением, необходимо подсчитать общее число квадратов отклонений I и вычесть из него I₂.