Вопрос 6. Модели, построенные с применением методов регрессионного анализа.
Случайные величины, соответствующие входным и выходным параметрам, могут представляться на разных уровнях, среди которых наиболее часто используются следующие четыре:
задана статистическая выборка a1..an, определяющая случайную величину набором значений, имеющих место в некоторой реализации случайного процесса;
известен закон распределения случайной величины;
заданы математическое ожидание и дисперсия;
известно только математическое ожидание.
Статистические методы – это совокупность способов сбора, анализа и интерпретации данных о свойствах объекта или совокупности объектов с целью получения теоретических или практических выводов.
Сущность статистических методов заключается в следующем. На основе эмпирических представлений о свойствах исследуемого объекта и в соответствии с целью исследования определяется состав и тип входных параметров х1,…хn и перечень выходных характеристик y1,…ym. Затем проводится эксперимент, целью которого является получение достаточно большой выборки связей между входными параметрами и выходными характеристиками объектов. Естественно полученные в результате эксперимента данные являются случайными числами. На основании этой выборки выбирается тип статистической модели (математические выражения, структура) и рассчитываются параметры модели.
Математическая статистика предлагает обширный набор моделей и методов установления статистических закономерностей, присущих исследуемым объектам. Наиболее распространённым из них является регрессионный анализ.
1)
|
y=f(x,z,F) – Случайная модель в которой переход из одного состояния в другое происходит в случайные моменты времени и непредсказуемы |
2)
|
y=f(x,z)+ε – детерминированный автомат, однозначно описываемый функцией, но имеются ошибки учитывающие влияние F «-» доказать адекватность можно только испытав в реальных условиях. |
3)
|
y=f(x)+ε – учитывают только управляющие воздействия «-» недостаточно точна не учитывает внешние воздействия «+» можно испытать в лаборатории |
Основная – вторая модель!
Модели объектов учитывают целенаправленные управляющие воздействия исполнительных устройств и контролируемые воздействия окружающей среды. Неконтролируемые воздействия окружающей среды приводят к появлению ошибок (в модели указываются в виде шума ). Уравнение, связывающее входные переменные с выходными, выглядит следующим образом:
y=f(x1,…,xk,b1,…,bk)+ (1),
где xi–i-тая входная переменная,
bi
– i-тый
параметр регрессионного уравнения,
i=1..k.
Если функция f(x1,…,xk,b1,…,bk) линейна относительно искомых параметров b1,…,bk, она может быть представлена в следующем виде:
f(x1,…xk,b1,…bk)=
φi
(x), (2)
где I(x) – некоторая заданная функция от хi, i=1..k .
Для удобства обычно принимают 1=1.
Чаще всего регрессионное уравнение представляют в виде степенного полинома конечной степени:
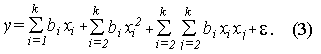
Введём
фиктивные переменные: х1=1,
х2k+1=xk+1,…,
x2k=x2k-1,
x2x3=x2k,…
В этом случае уравнение регрессии будет иметь следующий вид:
