Глава 9. Корреляционный анализ

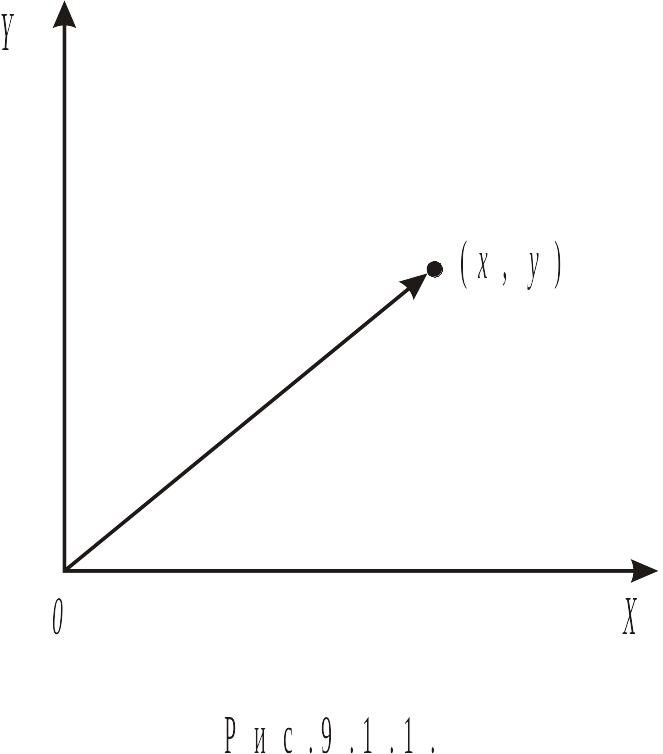9 .1. Системы случайных величин. В практическом применении теории вероятностей часто приходится сталкиваться с задачами, в которых результат описывается двумя или более случайными величинами, образующими комплекс, или систему. При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией. Например, систему двух случайных величин (X, Y) можно изобразить случайной точкой или случайным вектором на плоскости с координатами X и Y (рис.9.1.1).

Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств X < x и Y < y:

. (9.1.1)

Д ругими словами, если для геометрической интерпретации пользоваться образом случайной точки (рис.9.1.2), то функция распределения есть вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной в точке (x, y). Сформулируем свойства этой функции.

1. ,Функция распределения есть неубывающая функция обоих своих аргументов.

2. Всюду на функция распределения равна 0: .

3. П ри одном из аргументов, равном , функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу: , .

4. Если оба аргумента равны , функция распределения системы равна единице: .

Выведем выражение для попадания случайной точки (X,Y) в пределы заданной области D - , - на плоскости xOy, если эта область представляет собой прямоугольник R со сторонами, параллельными координатным осям, ограниченный абсциссами α и β и ординатами γ и δ (рис.9.1.3). Условимся включать в прямоугольник его нижнюю и левую границы и не включать верхнюю и правую, тогда событие будет равносильно произведению двух событий: и . Очевидно, что:

.(9.1.2)

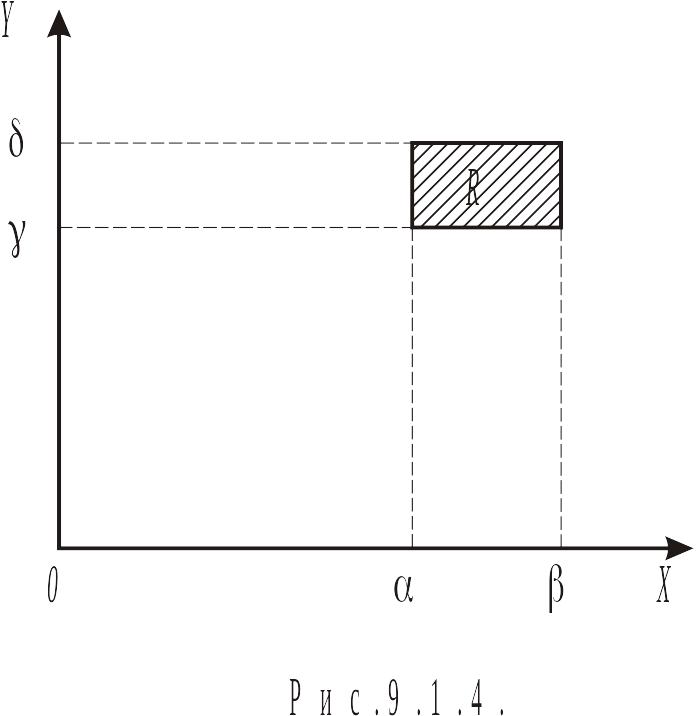
На практике основное значение имеют системы непрерывных случайных величин, распределение которых характеризуют плотностью распределения. Определим плотность распределения как предел отношения вероятности попадания случайной величины на малую область к площади этой области при ее неограниченном уменьшении (рис.9.1.4). Для простоты, в качестве области рассмотрим прямоугольник, тогда вероятность попадания случайной величины в произвольный прямоугольник определяется по формуле (9.1.2):

. (9.1.3)

Разделим вероятность попадания случайной величины в прямоугольник на и перейдем к пределу при и :

. (9.1.4)

Предположим, что функция F(x, y) не только непрерывна, но и дифференцируема: тогда правая часть (9.1.4) представляет собой вторую смешанную производную функции F(x, y) по x и y. Обозначим эту производную f (x, y):

. (9.1.5)

Функция f (x, y) называется плотностью распределения системы, а элемент вероятности, по аналогии с распределением одной случайной величины, запишется: f (x, y)dx dy.

Пользуясь понятием элемента вероятности, легко вывести выражение для вероятности попадания случайной точки в произвольную область D:

, (9.1.6)

а, воспользовавшись формулой (9.1.6), выразим функцию распределения системы F(x, y) через плотность распределения f (x, y):

. (9.1.7)

Введем теперь числовые характеристики для системы двух случайных величин.

Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения X^k на Y^s:

. (9.1.8)

Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:

, (9.1.9)

где , .

Выпишем формулы, служащие для непосредственного подсчета моментов. Для прерывных случайных величин:

, (9.1.10)

, (9.1.11)

где - вероятность того, что система (X, Y) примет значения (x_i, y_j), а суммирование распространяется по всем возможным значениям случайных величин X, Y. Для непрерывных случайных величин:

, (9.1.12)

, (9.1.13)

где f (x, y) - плотность распределения системы.

Помимо чисел k и s, характеризующих порядок момента по отношению к отдельным величинам, рассматривается еще суммарный порядок момента k + s, равный сумме показателей степеней при X и Y.

Первые начальные моменты представляют собой математические ожидания величин X и Y, входящих в систему:

,

.

Кроме этого на практике широко применяются еще вторые центральные моменты системы. Два из них представляют дисперсии величин X и Y:

,

,

характеризующие рассеивание случайной точки в направлении осей Ох и Оy. Особую роль, как характеристика системы, играет второй смешанный центральный момент:

,

то есть математическое ожидание произведения центрированных величин, для которого введено особое обозначение:

. (9.1.14)

Характеристика K_xy называется корреляционным моментом случайных величин Х и Y. Для прерывных случайных величин он выражается формулой

, (9.1.15)

а для непрерывных – формулой:

. (9.1.16)

Корреляционный момент описывает связь между случайными величинами. Если его значение отлично от нуля, то это является признаком наличия зависимости между случайными величинами Х и Y. Из формулы (9.1.14) видно, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин (Х, Y) весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины (Х, Y). Поэтому для характеристики связи между величинами (Х, Y) в чистом виде переходят от момента K_xy к безразмерной характеристике:

, (9.1.17)

где σ_x, σ_y – средние квадратические отклонения величин Х и Y. Эта характеристика называется коэффициентом корреляции величин Х и Y. Очевидно, что коэффициент корреляции обращается в нуль одновременно с корреляционным моментом, следовательно, для независимых случайных величин коэффициент корреляции равен нулю.

Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную, которая заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (убывать) по линейному закону: Y = aX + b.

Оценка коэффициента корреляции по выборочным наблюдениям рассчитывается по формуле:

, (9.1.18)

или

, (9.1.19)

где , - средние арифметические, а s_x и s_y – выборочные оценки средне квадратичного отклонения анализируемых признаков. В формуле (9.1.19) числитель представляет собой оценку среднего значения попарных произведений центральных отклонений, получившую название ковариации и обозначаемого обычно cov {x, y}. Таким образом, в генеральных совокупностях х и y коэффициент корреляции:

. (9.1.20)

Величина коэффициента корреляции может принимать значения в интервале от –1 до +1. Эти крайние случаи соответствуют функциональной прямолинейной связи между признаками: обратной, когда r = -1, и прямой при r = +1. При отсутствии прямолинейной связи r = 0, промежуточные величины r соответствуют разной степени тесноты связи. При линейной связи на точечном графике, отражающем эту связь между значениями нормально распределенных величин х и y, корреляционное поле точек имеет вид более или менее вытянутого эллипса. По мере увеличения тесноты связи к он превращается в прямую линию (рис.9.1.4). При r = 0 корреляционное поле точек имеет форму круга.

9.2. Оценки и значимость коэффициента корреляции. Коэффициент корреляции r, вычисляемый по выборочным данным, является точечной оценкой его генерального значения, которое характеризует степень связи между признаками в генеральных совокупностях. В силу этого, даже при отсутствии связи оценка r обычно отлична от нуля, поэтому необходимо проводить также оценку значимости связи, имея в виду связь в генеральных совокупностях, а не в рамках проанализированных выборок.

Как всякая оценка r является величиной случайной и, следовательно, она может быть охарактеризована стандартным отклонением, именуемым ошибкой коэффициента корреляции. Обычно оценку ошибки коэффициента корреляции вычисляют по формулам при n > 100:

, (9.2.1)

или при n < 100:

. (9.2.2)

Для проверки нулевой гипотезы H₀: r = 0 против альтернативы H₁: прибегают к вычислению статистики t-Стьюдента:

, (9.2.3)

и если (t_α берется при n < 100 для ν = n – 1, при n > 100 для ), то H₀ отвергается, и с соответствующим уровнем значимости делается утверждение о наличии линейной связи.

Подобный способ оценки значимости коэффициента корреляции не является безукоризненным, особенно если оцениваемый коэффициент корреляции по абсолютной величине близок к единице (при этом распределение оценок r заметно отличается от нормального, а распределение отношений - от распределения t-Стьюдента). Более правильную оценку значимости r можно получить, если воспользоваться преобразованием z, предложенным Р.А.Фишером, где:

, (9.2.4)

где - табулированная функция. Преимущество случайной величины z по сравнению с r состоит в том, что z распределена приближенно нормально практически независимо от величины среднего значения μ_z и объема выборок n. К тому же среднее квадратическое отклонение σ_z, характеризующее варьирование z, определяется только объемом выборок n и не зависит от z:

. (9.2.5)

Поскольку гипотезе H₀: r = 0 соответствует H₀: μ_z = 0, то критерий проверки гипотез сводится к вычислению:

(9.2.6)

и сравнению полученного t с t_α для . При можно утверждать, что связь есть.

К примеру, для r = +0,70 (пример приведен в разделе 7,3) z = 0,8673. При n = 6 , что меньше t_0,05 = 1,96, поэтому утверждать, что μ_z значимо отличается от нуля, нет оснований, а, следовательно, нельзя считать статистически значимым и коэффициент корреляции.

Использование преобразования z дает возможность корректного получения интервальной оценки r. Для этого следует найти доверительные границы μ_z, что легко сделать, принимая во внимание нормальность распределения z и то, что математическое ожидание для z примерно равно (здесь ρ - значение коэффициента корреляции для генеральной совокупности)

:

, (9.2.7)

(t_α , берется для ). Затем можно найти те значения r, которые соответствуют нижней и верхней границам для μ_z. Так, для упомянутого примера получим ( n = 6; r = 0,70; z = 0,8673; α = 0,05): , т. е. -0,33<μ_z<1,93. Произведя обратную операцию, найдем, что доверительные границы коэффициента корреляции оказываются равными . Другими словами, при α = 0,05 генеральное значение коэффициента корреляции может находится в очень широкой области, включающей не только практически все положительные значения, большую часть отрицательных, но и может иметь нулевое значение.

Все операции по проверке значимости выборочного значения коэффициента корреляции можно упростить, заранее вычислив для различных абсолютных значений оценок r минимальные объемы корреляционных рядов (пар сопряженных значений x и y), обеспечивающих возможность утверждать с уровнем значимости α, что , то есть утверждения наличия линейной связи. Как следует из формулы (9.2.6), чтобы отклонить Н₀: μ_z = 0 для заданного z (и r), нужно по меньшей мере обеспечить равенство t = t_α. Тогда искомое n_α определится по формуле:

. (9.2.8)

Так, коэффициент корреляции, выборочная оценка которого по модулю равна 0,70, можно считать статистически значимым с α = 0,05, если n по крайней мере равно 9.

9.3. Величина и смысл коэффициента корреляции. При корреляционных связях абсолютная величина ρ обычно отлична от единицы, в связи с чем перед исследователями возникает проблема качественной оценки степени тесноты связи между изучаемыми признаками, т.е. при каких ρ связь можно считать тесной, а при каких - слабой.

Общепринятой градации для такой оценки не существует, но некоторые условные рекомендации дать можно. Они основываются на том, что квадрат коэффициента корреляции является оценкой в долях единицы той части варьирования одного признака, которая связана с варьированием другого признака. Если, например, связь между содержанием в грунте глинистых частиц и максимальной молекулярной влагоемкостью характеризуется коэффициентом корреляции r = 0,70, то это можно интерпретировать так, что на 0,70², или на 49 %, варьирование содержания глинистых частиц связано с варьированием максимальной молекулярной влагоемкости, а на 51 % варьирование этих признаков осуществляется взаимно независимо.

Величина квадрата коэффициента корреляции может иметь самостоятельный интерес, поэтому ее иногда выделяют в качестве особого параметра, именуемого коэффициентом детерминации. Если, с учетом сказанного оценить разные абсолютные значения коэффициентов корреляции, то за весьма тесную связь условно можно считать такую, при которой |r| > 0,85 (варьирование признаков взаимосвязано приблизительно на 75 % и более), за тесную связь - когда (взаимосвязанная вариация признаков лежит в пределах 75-50 %), и слабой можно считать связь, если r < 0,7 (варьирование одного признака менее чем на 50 % связано с варьированием другого признака).

Указанные значения для качественной характеристики степени связи условны, однако в определенном смысле и абсолютны, так как установлены безотносительно к изучаемым явлениям, исходя лишь из особенностей самого коэффициента корреляции.

Нужно иметь в виду, что строго прямолинейные связи между свойствами природных объектов и явлений - достаточно редкий случай. Обычно даже там, где связь считается прямолинейной, в действительности имеет место некоторая криволинейность, которую либо не замечают, либо ею пренебрегают. В силу этого коэффициент корреляции, являющийся мерой прямолинейной связи, обычно отличается от единицы, даже если связь функциональная, но не прямолинейная.

Еще более важным обстоятельством, определяющим величину коэффициента корреляции, является то, что каждый изучаемый признак часто находится в сложной взаимосвязи с большим числом других признаков, прямо или косвенно оказывающих влияние на его варьирование. В силу этого связь между каждой парой взятых признаков оказывается затушеванной влиянием всех прочих неучитываемых признаков, роль которых может быть разной, и, как следствие, коэффициент корреляции будет то больше, то меньше отличаться от единицы.

Так, связь между величиной максимальной гигроскопичности и содержанием физической глины для некоторых грунтов обычно велика, хотя и осложнена недоучетом минерального состава, характера поглощающего комплекса и некоторых других явлений, так или иначе сказывающихся на величине максимальной гигроскопичности.