2.3. Визуализация
В окне «График» строиться зависимость значения интеграла от количества разбиений n (n изменяется на интервале [10,200] с шагом 10).
Код выглядит следующим образом:
procedure TForm4.Button2Click(Sender: TObject);
var i,n,n1:integer;
h,a,b,s,y,x,r:real;
begin
n1:=strtoint(edit1.Text);
n:=10;
a:=StrToFloat(form2.edit1.text);
b:=StrTofloat(form2.edit2.text);
chart1lineseries1.Clear;
while n<=200 do // Внешний цикл с предусловием, выполняется до тех пор, пока число разбиений не достигнет либо не превысит 200
begin
h:=(b-a)/n; // Рассчитываем шаг
x:=b; s:=0;
for i:=n downto 1 do // Вложенный цикл с параметром, вычисляет значении интеграла.
begin
y:=Form1.Z(x);
s:=s+y;
x:=x-h;
end;
r:=s*h;
Chart1LineSeries1.addxy(n,r); // Строим точку. Х – число разбиений (n) У – значение интеграла (r)
n:=n+n1; // Увеличиваем число разбиений на заданный шаг.
end;
2.4. Вычислительный эксперимент
Запускаем нашу программу. Открывается главное окно. На нем обозначены следующие пункты меню: «Вычисление», «Об авторе», «О программе», «Выход». В пункт «Вычисление» входит еще три подпункта: «Ввод промежутка», «Вычислить интеграл», «Построить график».
Рисунок 9 - главное окно
Открываем подпункт «Ввод промежутка».
Рисунок 10 - Ввод промежутка
При открытии наш промежуток введен заранее. Нам остается лишь ввести Число разбиений и закрыть данное окно.
Далее открываем следующий подпункт «Вычислить интеграл», где нажимаем на кнопку «Вычислить».
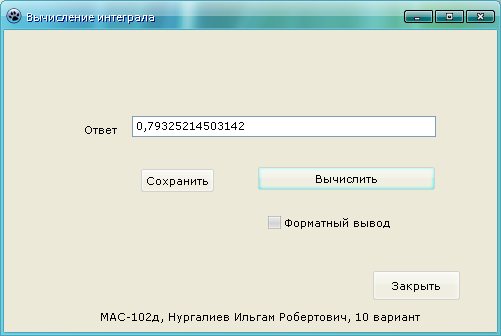
Рисунок 11 - Вычисление интеграла
Приложение выдает нам следующий ответ: 0,79325214503142. В случае, если мы активируем флажок «Форматный вывод» то мы увидим следующее значение: 0,7933.
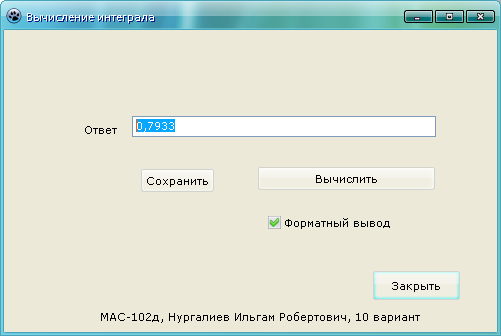
Рисунок 12 - Форматный вывод
Далее проверяем работоспособность кнопки «Сохранить». Кликнем на нее. В папке с нашим приложением появляется текстовый файл save.txt, в который сохраняется значение нашего интеграла.
Рисунок 13 - Сохранение результата
Аналогичные действия выполняются и для форматного вывода.
Далее необходимо построить график. Открываем подпункт «Построить график», вводим шаг, и наживаем кнопку построить, наблюдаем следующую картину:
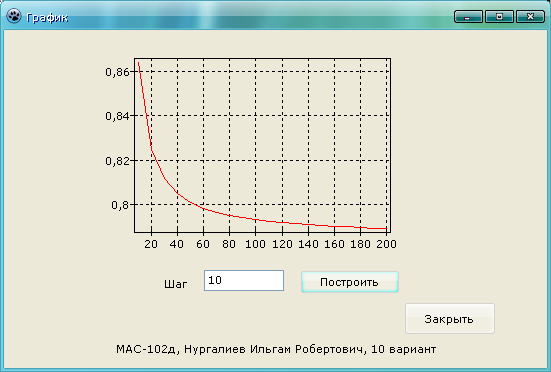
Рисунок 14 – График
Следующим шагом проверяем пункты меню «Об авторе» и «О программе». При их открытии мы видим информации о разработчике, и о назначении нашей программы. Рисунки данных окон были предоставлены ранее.
2.5 Сравнение результатов выполнения приложения с результатом, полученным в математическом пакете
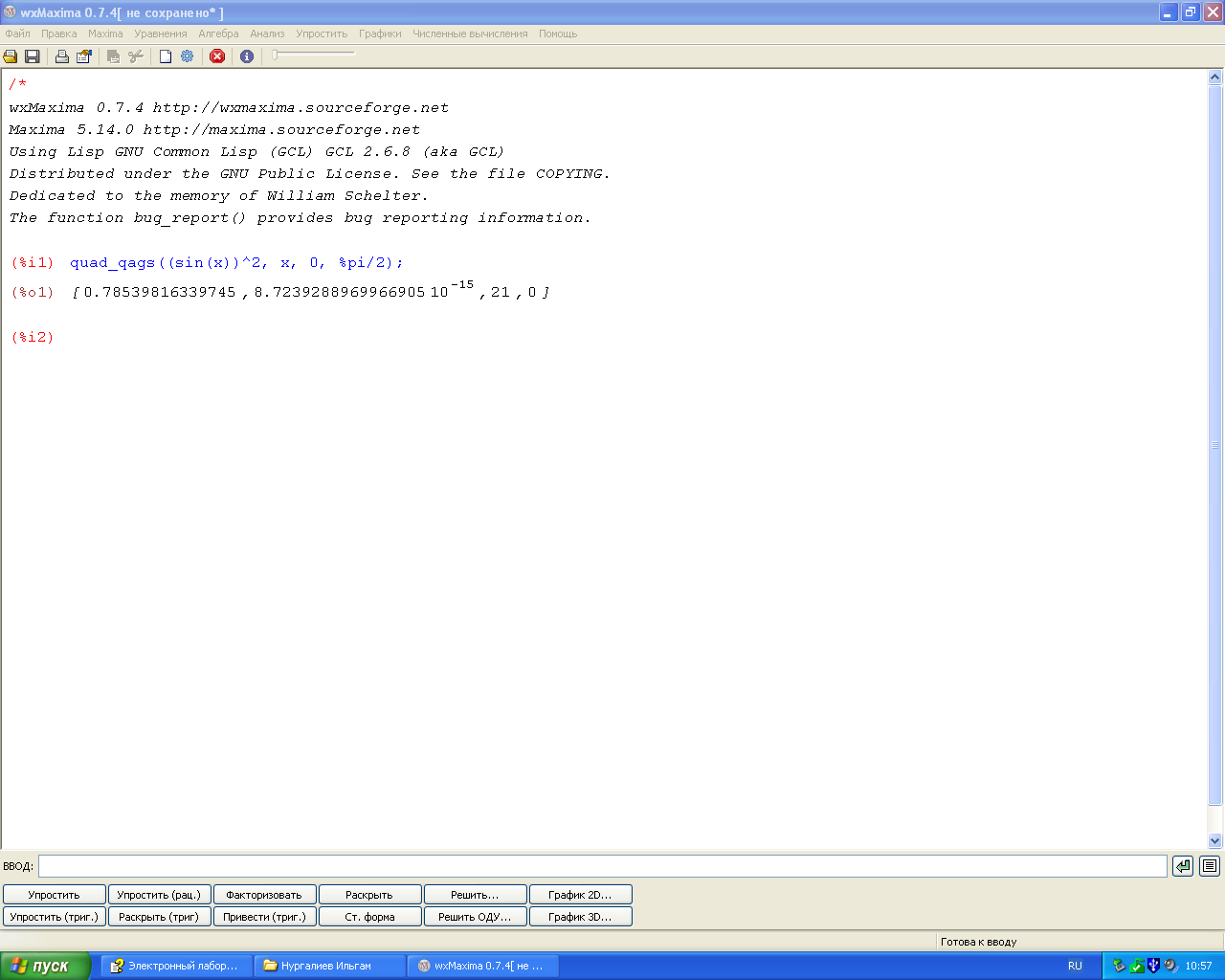
Рисунок 15 - Результат Maxima
Из данного рисунка видно, что результат, полученный в wxMaxima составляет 0,78539816339745. Наше приложение выдало нам результат 0,79325214503142. Погрешность составляет 0.00785398163397. Это говорит о том, что ответы имеют близкое значение. При увеличении числа разбиений в программе результат становиться все ближе у полеченному в wxMaxima. Это показывает нам, что мы можем лишь стремиться к приближенному ответу, и то что метод «правых прямоугольников» не достаточно точный.
Заключение
Было создано приложение, которое вычисляет определенный интеграл от функции y=sin2x на интервале [0;π/2]. Для расчетов использовался метод «правых прямоугольников». Приложение содержит 5 окон, а так же текстовое меню, позволяющее нам выполнить основные операции.
Проведена визуализация. Программа строит график зависимости значения интеграла от числа разбиений на промежутке [10;200] и шагом 10. Пользователь так же может ввести свой собственный шаг.
Результат, полученный в приложении, сравнили с результате полученном в математическом пакете. Погрешность составила 0.00785398163397. Это свидетельствует о недостаточной точности данного метода.