3 Выбор метода контроля (теоретический анализ акустического тракта)

Из вывода, полученного в пункте 2 следует, что контроль сварного шва таврового соединения будет вестись эхо-импульсным методом контроля, так как данный метод обладает простотой реализации и достаточной помехоустойчивостью, метод обладает преимуществом одностороннего доступа к поверхности объекта контроля, имеет наибольшую чувствительность к выявлению внутренних дефектов. Этим методом контролируют около 90% всех сварных соединений толщиной 4 мм и более. Прозвучивание стыкового сварного шва производится наклонным преобразователем по поверхности полки.

Дефекты типа трещин и пор будем контролировать прямым и однократно отраженным лучами наклонным преобразователем, а непровары в корне шва – прямым лучом.

В сварных швах возможны дефекты в виде пор, трещин и непроваров в корне шва. Эти дефекты моделируются сферой, диском и бесконечной полосой.

Рассмотрим схему обнаружения трещин:

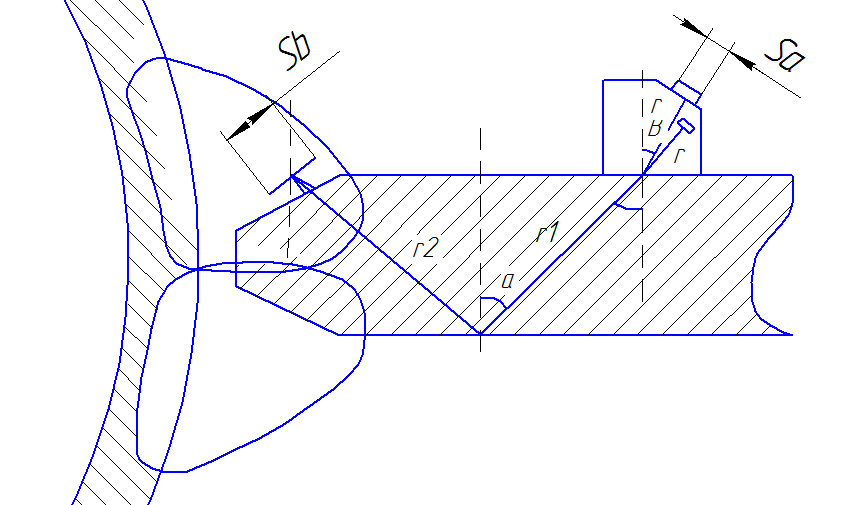
Рисунок 3.2 – Схема для расчета акустического тракта при контроле

наклонным преобразователем однократно-отраженным лучом

Уравнение акустического тракта для диска площадью S_b имеет следующий вид:

(3.1)

где – коэффициент прохождения через границу раздела;

– площадь ПЭП;

– площадь отражателя;

– номинальный угол ввода преобразователя;

– номинальный угол призмы преобразователя;

r – длина пути УЗ до дефекта в изделии;

– путь в призме до мнимого источника;

δ – коэффициент затухания в изделии;

δ_пр – коэффициент затухания в материале призмы.

R_no – действительный путь в призме

Исходя из известных параметров, преобразуем формулу 3.1.

Приведенный путь ультразвука в призме преобразователя будет определяться выражением:

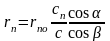(3.2)

где - действительный путь в призме;

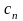и с – скорости УЗ-волн в призме и изделии.

Длина пути до дефекта в изделии

(3.3)

Т.к. дефект может быть ориентирован под любым углом, то

(3.4)

Исходя из формул (3.3); (3.4) выражение (3.1) примет вид:

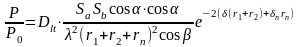(3.5)

Рассмотрим схему обнаружения пор:

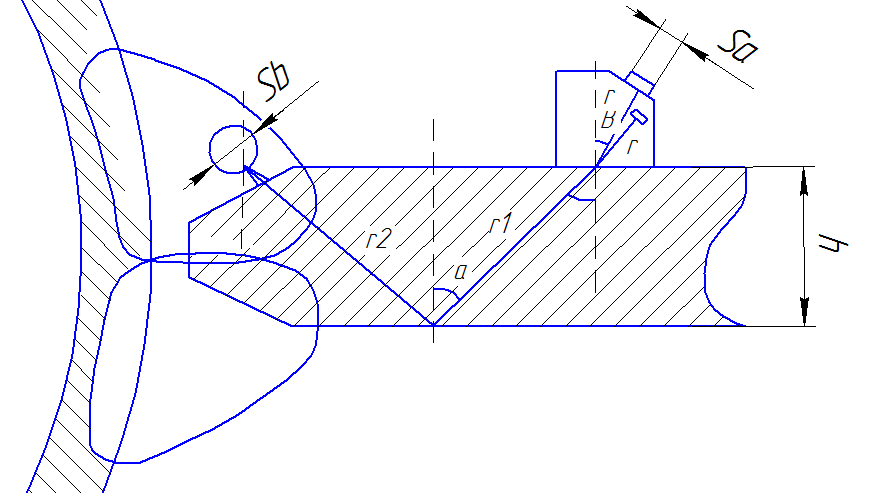
Рисунок 3.3. – Схема обнаружения пор

Уравнение акустического тракта для сферы имеет вид:

(3.6)

С учетом формулы (3.2) и (3.4) выражении (3.6) примет вид:

(3.7)

С учетом всех известных формул, выражение (3.7) примет вид:

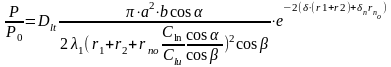(3.8)

Рассмотрим схему обнаружения непроваров:

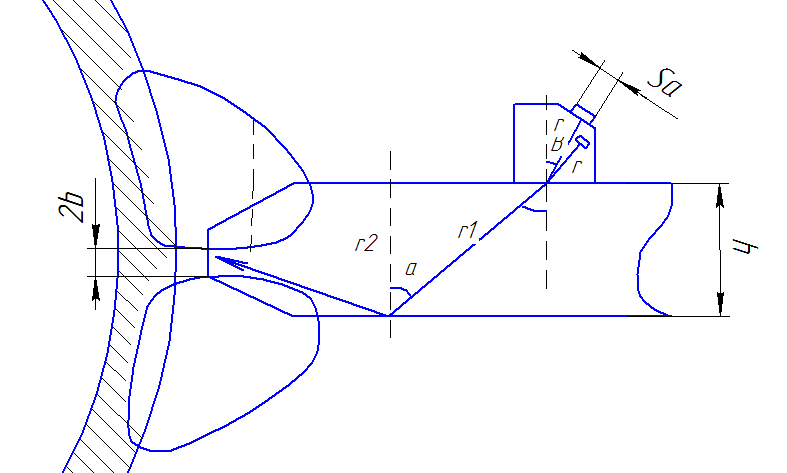
Рисунок 3.4 – Схема обнаружения непроваров

Уравнение акустического тракта для бесконечной полосы:

(3.9)

Уравнение акустического тракта для бесконечной полосы имеет вид:

(3.10)

С учетом формулы всех известных выражений (3.10) примет вид:

(3.11)

Таким образом, был проведен анализ акустического тракта в общем виде, для получения конкретных выражений необходимо подставить в выражения (3.5), (3.8), (3.11) значение параметров пьезопреобразователя, которые будут рассчитаны далее.