3.3 Исследование сау по критерию Найквиста
Критерий Г. Найквиста позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы (АФЧХ) оценить устойчивость замкнутой системы с отрицательной обратной связью.
АФЧХ можно построить на комплексной плоскости [+1; j] или в полярной системе координат, если откладывать угол фазы φ() и в этом направлении откладывать вектор длиной А().
Амплитуда передаточной функции разомкнутой системы АРАЗ() равна произведению амплитуд отдельных звеньев, а фаза φРАЗ() – сумме фаз звеньев:
; (3.25)
. (3.26)
Найти амплитуду А() и фазу φ() можно по вещественной U(ω) и мнимой V(ω) составляющим частотной передаточной функции W(jω) звена.
Амплитуда А() и фаза φ() частотной передаточной функции W(jω):
; (3.27)
. (3.38)
Вещественную UРАЗ(ω) и мнимую VРАЗ(ω) составляющую частотной передаточной функции разомкнутой системы WРАЗ(jω) можно определить по амплитуде АРАЗ() и фазе φРАЗ():
; (3.29)
. (3.30)
Формулировка критерия Найквиста
Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы на комплексной плоскости [+1; j] при изменении частоты от 0 до не охватывала точку с координатами (-1; j0). Если АФЧХ разомкнутой системы проходит через точку с координатами (-1; j0), то система находится на границе устойчивости.
Для построения АФЧХ разомкнутой системы необходимо перейти к частотной форме записи передаточной функции разомкнутой системы.
Передаточная функция разомкнутой системы:
; (3.31)
. (3.32)
Проведем преобразования, выделив общий коэффициент усиления разомкнутой системы и представив знаменатель передаточной функции двигателя постоянного тока как произведение двух слагаемых:
; (3.33)
; (3.34)
. (3.35)
Запишем выражения амплитуд А() и фаз φ() частотных передаточных функции для каждого звена (табл. 3.2). Вычисляем значения амплитуд А() и фаз φ() при изменении часты от 0 до значения, при котором UРАЗ(ω) и VРАЗ(ω) станут равны нулю. Также вычислим амплитуду АРАЗ() и фазу φРАЗ() передаточной функции разомкнутой системы, а также вещественную UРАЗ(ω) и мнимую VРАЗ(ω) составляющую частотной передаточной функции разомкнутой системы WРАЗ(jω). Шаг изменения частоты принимаем произвольный с учетом удобства восприятия графика. Вычисления проводим в MS Excel.
Таблица 3.2
Выражения амплитуд А() и фаз φ() передаточных функции звеньев системы
Передаточная функция звена |
Амплитуда А() |
Фаза φ() |
|
|
|
|
|
|
|
|
|
Таблица 3.3
Значения амплитуд А() и фаз φ() передаточных функции звеньев системы
Частота ω |
Амплитуды звеньев |
Фазы звеньев |
Амплитуда WРАЗ(jω) |
Фаза WРАЗ(jω) |
Действит. часть WРАЗ(jω) |
Мнимая часть WРАЗ(jω) |
||||
A1(ω) |
A2(ω) |
A3(ω) |
φ1(ω) |
φ2(ω) |
φ3(ω) |
AРАЗ(ω) |
φРАЗ(ω) |
UРАЗ(ω) |
VРАЗ(ω) |
|
0,0 |
2,34 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
2,34 |
0,00 |
2,34000 |
0,00000 |
1,0 |
2,14 |
0,97 |
0,96 |
-0,20 |
-0,06 |
-0,09 |
1,99 |
-0,35 |
1,86907 |
-0,67583 |
2,0 |
1,74 |
0,90 |
0,85 |
-0,38 |
-0,11 |
-0,19 |
1,34 |
-0,68 |
1,04721 |
-0,84280 |
4,0 |
1,14 |
0,73 |
0,63 |
-0,67 |
-0,22 |
-0,36 |
0,52 |
-1,25 |
0,16323 |
-0,49836 |
6,0 |
0,82 |
0,58 |
0,48 |
-0,88 |
-0,32 |
-0,51 |
0,22 |
-1,71 |
-0,03187 |
-0,22272 |
8,0 |
0,63 |
0,47 |
0,38 |
-1,01 |
-0,42 |
-0,65 |
0,11 |
-2,08 |
-0,05394 |
-0,09728 |
10,0 |
0,51 |
0,39 |
0,31 |
-1,11 |
-0,51 |
-0,76 |
0,06 |
-2,37 |
-0,04428 |
-0,04302 |
12,0 |
0,43 |
0,33 |
0,26 |
-1,18 |
-0,59 |
-0,85 |
0,04 |
-2,61 |
-0,03227 |
-0,01892 |
14,0 |
0,37 |
0,29 |
0,23 |
-1,23 |
-0,66 |
-0,92 |
0,02 |
-2,81 |
-0,02293 |
-0,00785 |
16,0 |
0,32 |
0,26 |
0,20 |
-1,27 |
-0,73 |
-0,99 |
0,02 |
-2,98 |
-0,01634 |
-0,00266 |
18,0 |
0,29 |
0,23 |
0,18 |
-1,30 |
-0,79 |
-1,04 |
0,01 |
-3,12 |
-0,01178 |
-0,00021 |
20,0 |
0,26 |
0,21 |
0,16 |
-1,33 |
-0,84 |
-1,08 |
0,01 |
-3,25 |
-0,00862 |
0,00092 |
22,0 |
0,24 |
0,19 |
0,15 |
-1,35 |
-0,89 |
-1,12 |
0,01 |
-3,35 |
-0,00641 |
0,00139 |
24,0 |
0,22 |
0,17 |
0,13 |
-1,37 |
-0,93 |
-1,15 |
0,01 |
-3,45 |
-0,00484 |
0,00153 |
26,0 |
0,20 |
0,16 |
0,12 |
-1,38 |
-0,97 |
-1,18 |
0,00 |
-3,53 |
-0,00371 |
0,00152 |
28,0 |
0,19 |
0,15 |
0,12 |
-1,39 |
-1,00 |
-1,21 |
0,00 |
-3,60 |
-0,00289 |
0,00143 |
30,0 |
0,17 |
0,14 |
0,11 |
-1,41 |
-1,03 |
-1,23 |
0,00 |
-3,67 |
-0,00227 |
0,00132 |
32,0 |
0,16 |
0,13 |
0,10 |
-1,42 |
-1,06 |
-1,25 |
0,00 |
-3,73 |
-0,00181 |
0,00120 |
34,0 |
0,15 |
0,12 |
0,10 |
-1,42 |
-1,08 |
-1,27 |
0,00 |
-3,78 |
-0,00146 |
0,00108 |
36,0 |
0,15 |
0,12 |
0,09 |
-1,43 |
-1,11 |
-1,28 |
0,00 |
-3,82 |
-0,00119 |
0,00096 |
38,0 |
0,14 |
0,11 |
0,09 |
-1,44 |
-1,13 |
-1,30 |
0,00 |
-3,87 |
-0,00097 |
0,00086 |
40,0 |
0,13 |
0,11 |
0,08 |
-1,45 |
-1,15 |
-1,31 |
0,00 |
-3,91 |
-0,00081 |
0,00077 |
42,0 |
0,12 |
0,10 |
0,08 |
-1,45 |
-1,17 |
-1,32 |
0,00 |
-3,94 |
-0,00067 |
0,00069 |
44,0 |
0,12 |
0,10 |
0,07 |
-1,46 |
-1,18 |
-1,33 |
0,00 |
-3,97 |
-0,00057 |
0,00062 |
46,0 |
0,11 |
0,09 |
0,07 |
-1,46 |
-1,20 |
-1,34 |
0,00 |
-4,00 |
-0,00048 |
0,00056 |
48,0 |
0,11 |
0,09 |
0,07 |
-1,47 |
-1,21 |
-1,35 |
0,00 |
-4,03 |
-0,00041 |
0,00050 |
50,0 |
0,10 |
0,08 |
0,06 |
-1,47 |
-1,23 |
-1,36 |
0,00 |
-4,06 |
-0,00035 |
0,00046 |
52,0 |
0,10 |
0,08 |
0,06 |
-1,47 |
-1,24 |
-1,37 |
0,00 |
-4,08 |
-0,00030 |
0,00041 |
54,0 |
0,10 |
0,08 |
0,06 |
-1,48 |
-1,25 |
-1,38 |
0,00 |
-4,10 |
-0,00026 |
0,00037 |
56,0 |
0,09 |
0,08 |
0,06 |
-1,48 |
-1,26 |
-1,38 |
0,00 |
-4,13 |
-0,00023 |
0,00034 |
58,0 |
0,09 |
0,07 |
0,06 |
-1,48 |
-1,27 |
-1,39 |
0,00 |
-4,14 |
-0,00020 |
0,00031 |
60,0 |
0,09 |
0,07 |
0,05 |
-1,49 |
-1,28 |
-1,40 |
0,00 |
-4,16 |
-0,00017 |
0,00028 |
62,0 |
0,08 |
0,07 |
0,05 |
-1,49 |
-1,29 |
-1,40 |
0,00 |
-4,18 |
-0,00015 |
0,00026 |
64,0 |
0,08 |
0,07 |
0,05 |
-1,49 |
-1,30 |
-1,41 |
0,00 |
-4,20 |
-0,00014 |
0,00024 |
65,0 |
0,08 |
0,07 |
0,05 |
-1,49 |
-1,30 |
-1,41 |
0,00 |
-4,20 |
-0,00013 |
0,00023 |
По значениям вещественной UРАЗ(ω) и мнимой VРАЗ(ω) части частотной передаточной функции разомкнутой системы из таблицы 3.1 строим годограф Найквиста (рис. 3.2).
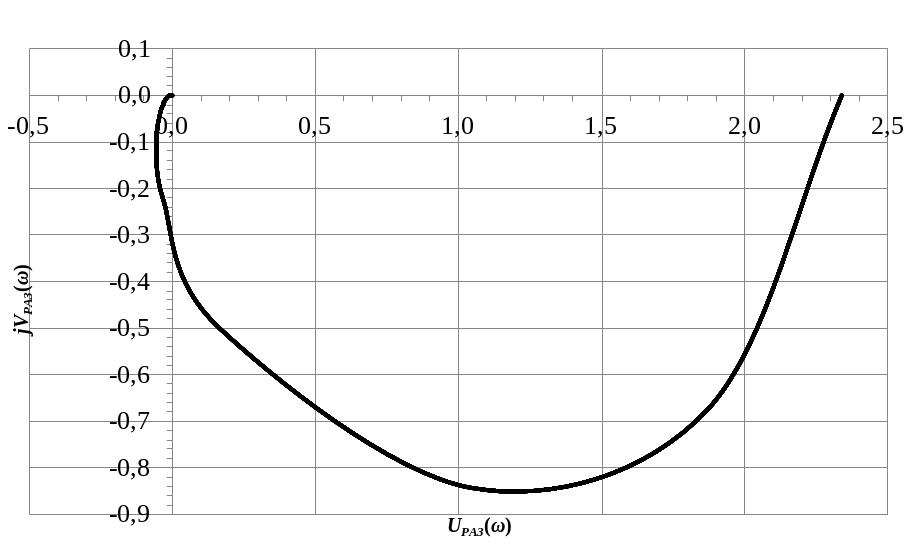
Рис. 3.2. Годограф Найквиста (АФЧХ)
Вывод: замкнутая система устойчива, так как АФЧХ разомкнутой системы не охватывает точку с координатами (-1; j0).