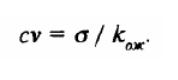14. Методы оценки риска. Способы управления риском.

Риск - вероятность того, что прогнозируемые события не произойдут (не осуществятся обещанные явные платежи, не произойдет прирост капитала) и реальные денежные потоки окажутся меньше прогнозируемых.

Чистый риск – нежелательные отклонения от желаемых значений (потеря капитала, недополучение явных платежей и т.д.)

Количественная оценка риска актива.

Рисковые активы характеризуются вероятностными значениями получения результата.

Если известны все возможные значения результата (значения дохода в абсолютном

выражении или относительное значение — доходность) и вероятности получения этих

значений (сумма вероятностей равна единице), то такое представление результата носит

название вероятностного распределения. Вероятностное распределение может быть представлено в виде таблицы или

графически. Например, если рассматривается владение недвижимостью ("актив А") и

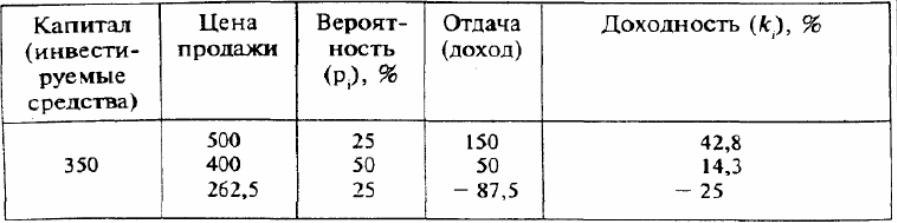
известны возможные цены продажи через год при различной ситуации в спросе (введение налога на недвижимость, ввод в эксплуатацию нового жилья и другие факторы могут повлиять на спрос), то вероятностное распределение может быть представлено в виде таблицы

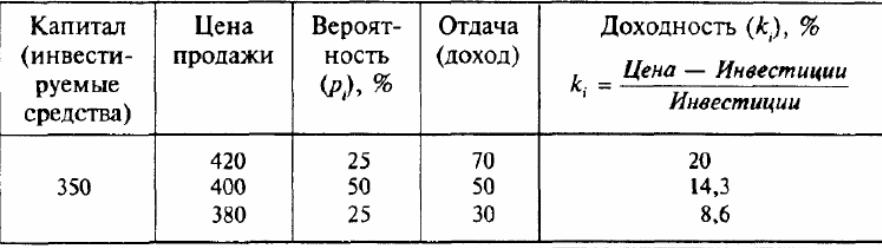
Непрерывное распределение вероятности

При предположении о возможности указать вероятность каждого исхода (в примере с активом А — указать вероятность его продажи по цене от 350 до 450 тыс. долл.) можно построить график непрерывного распределения вероятности

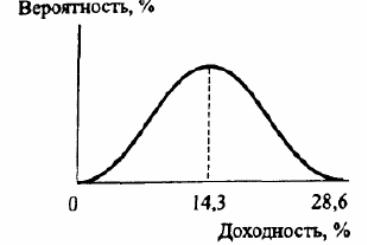
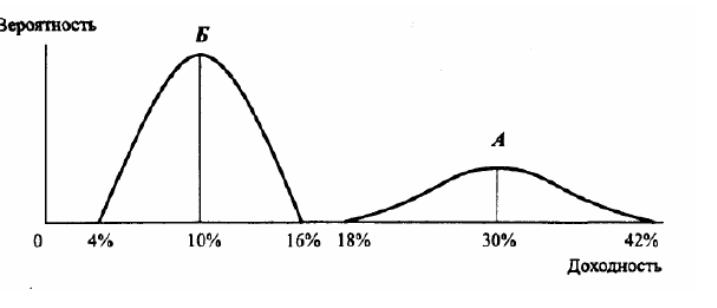
Рассмотрим актив В с следующими параметрами распределения

а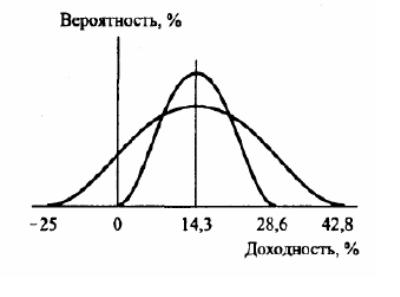 ктив В – более рискованный Нормальное вероятностное распределение

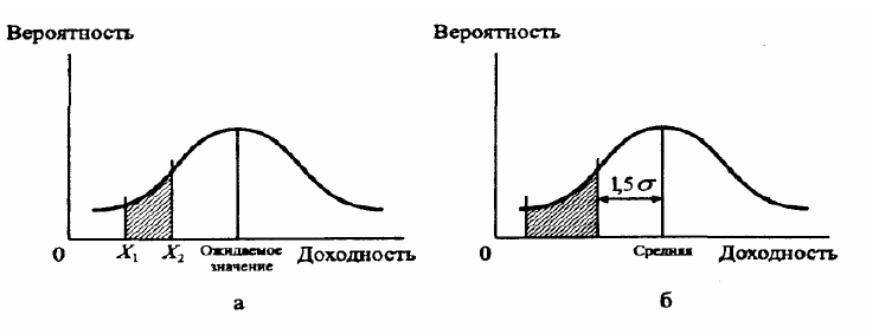
Мера риска

Для сравнения активов (реальных и финансовых) и принятия инвестиционных

решений необходима количественная оценка риска, позволяющая ранжировать активы.

В практике финансового менеджмента нашли применение несколько оценок риска:

1) дисперсия, как мера разброса возможных значений доходности;

14.

2) стандартное отклонение, как мера разброса, выраженная в тех же единицах, что и

результат (например, доходность);

3) коэффициент вариации для ранжирования активов с различными значениями

ожидаемой доходности.

Мерой разброса возможных результатов вокруг ожидаемого значения является

дисперсия (или вариация). Чем больше дисперсия, тем сильнее разброс. Дисперсия дискретного распределения рассчитывается по формуле

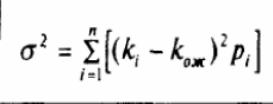
n — число возможных отклонений от ожидаемого значения

Дисперсия доходности есть сумма произведений всех возможных отклонений фактических значений доходности от ожидаемого значения на вероятность этого отклонения. Дисперсия измеряется в тех же единицах, что и результат (в процентах, если в качестве результата рассматривается доходность, и в денежных единицах, если в качестве результата рассматриваются денежные потоки — выручка, издержки, прибыль и т.д.), но возведенных в квадрат

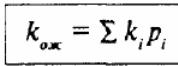
Для облегчения сравнения и анализа риска различных активов чаще используется квадратный корень из дисперсии — среднеквадратинеское (или стандартное) отклонение:

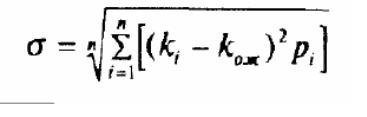
Если сравниваются активы, имеющие различную доходность, то по значению стандартного отклонения нельзя сделать вывод, какой из них является более рискованным. Для сравнения активов с различной доходностью по степени риска необходимо уравнять разброс с учетом доходности, т.е. рассчитать риск на единицу доходности. Более рискованным будет тот актив, по которому выше риск на единицу доходности. Таким нормированным показателем степени риска является коэффициент вариации (СV), как отношение стандартного отклонения к ожидаемому значению результата: