Метод главного критерия

В методе главного критерия в качестве в качестве целевой функции выбирается один из функционалов, например , наиболее полно отражающей цель решаемой задачи с точки зрения эксперта. Остальные требования к результату, описываемые критериями , учитываются с помощью введения необходимых дополнительных ограничений. Т.е., вместо задачи, определяемой соотношениями (3.1), решается другая, уже однокритериальная задача вид:

(3.6)

Таким образом, получили более простую задачу поиска максимума функции на новом допустимом множестве . Это множество получено из исходного множества Z, путем добавления ограничений вида . Эти соотношения показывают, что вместо поиска наибольших значений критериев выдвигаются требования на ограниченность их снизу на приемлемых уровнях.

Преимущество метода главного критерия:

1. Как правило, всегда удается определить единственный оптимальный вариант решения;

2. Не происходит взаимной компенсации частных критериев (в отличие от аддитивного критерия).

Недостатки:

1. Трудности (субъективизм) в определении главного критерия.

2. Трудности (субъективизм) в определении допустимых уровней .

Если главный критерий желательно уменьшить, то рассматривается задача о минимизации соответствующего функционала. Если значение какого-либо другого критерия желательно уменьшить, то соответствующее неравенство имеет форму «не больше» (≤).

Рассмотрим использование метода главного критерия для задачи сопоставления четырех вариантов под индивидуальную застройку по трем критериям (пример 3.2). Допустим, что главным критерием является K₃, а для 1-го и 2-го критериев допустимыми уровнями будут 50 и 7 соответственно. Т.е. нас устраивают участки, удаленные от городской черты не более чем на 50 километров и имеющие оценку привлекательности не ниже 7.

В данном случае новое допустимое множество .будет состоять из вариантов (2,3 и 4) , вариант 1 не вошел в это множество, поскольку значение 2-го критерия, равное 6, для него ниже допустимого уровня 7 .

Для этих вариантов (2,3 и 4) выбираем тот, где K₃ минимально, это вариант 3. Следовательно, 3-ий вариант является оптимальным при заданных уровнях значимости и данном главном критерии.

Метод главного критерия имеет простую геометрическую интерпретацию (рис.3.2).

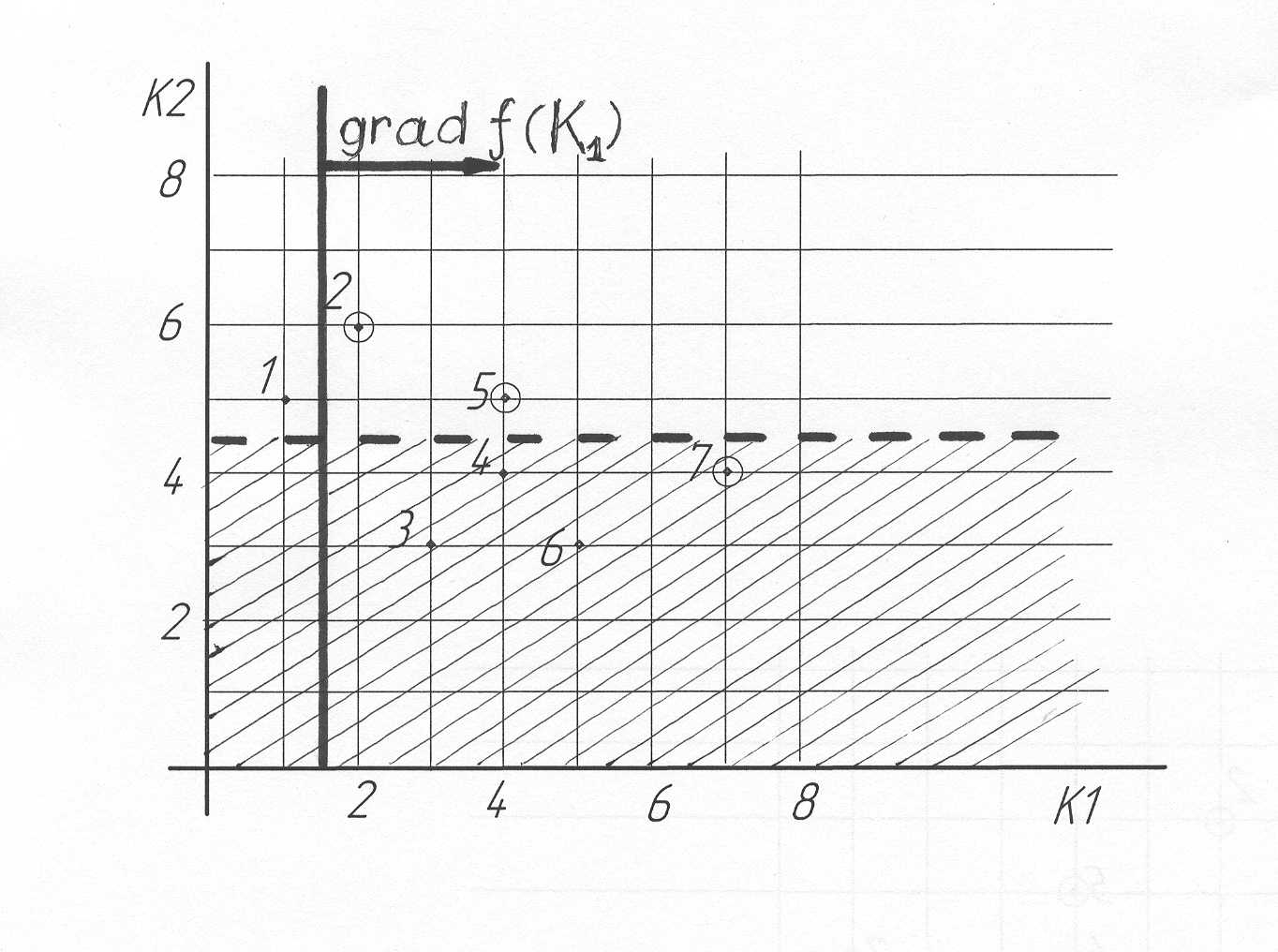
Рис.3.2

Рассмотрим решение примера 3 этим методом. Будем полагать, что главным критерием является K₁ , а для второго критерия (K₂) допустимый уровень t₂=5. Таким образом, имеем задачу по нахождению максимума функции . У функции линии уровня являются прямыми вида , а градиент - единичный вектор параллельный оси . Т.е., из двух альтернатив, лучше та, у которой точка, соответствующая альтернативе, расположена правее. Условие приводит к ограничению на альтернативы: в допустимое множество попадают только, те которые лежат выше прямой . Область недопустимых значений на рисунке заштрихована (граница, показанная пунктиром, принадлежит допустимому множеству). Таким образом, оптимальной стратегией будет, та которой соответствует самая правая точка, принадлежащая области допустимых значений. Очевидно, что это точка 5.