5.4.4. Определение количественных характеристик надежности по графу состояний

В предыдущих разделах были описаны правила, позволяющие из графа состояний найти в преобразованиях Лапласа вероятности пребывания восстанавливаемой системы в данный момент времени в любом состоянии и вероятности попасть в любое состояние в течение времени t. Эти вероятности позволяют найти основные количественные характеристики надежности системы, например: функцию и коэффициент готовности, вероятность безотказной работы, среднее время безотказной работы, наработку на отказ, а также среднее время восстановления. Рассмотрим особенности определения основных характеристик.

• Вычисление функции готовности

Функция готовности К_г(t) является вероятностью застать систему в исправном состоянии в любой момент времени, поэтому для ее определения необходимо найти сумму вероятностей всех исправных состояний системы. Для определения К_г(t) из графа состояний по методике, изложенной в разд. 5.4.1, находятся преобразования Лапласа вероятностей всех исправных или всех отказовых состояний и определяется преобразование Лапласа функции готовности по одной из следующих формул:

где Р_i(s) — преобразование Лапласа вероятности пребывания системы в данный момент времени в исправном (или отказовом) состоянии, соответствующем i-му узлу графа;

n — общее число узлов графа, равное числу всех возможных состояний системы;

k — число узлов графа, соответствующих исправным состояниям системы.

Если число отказовых состояний системы меньше числа исправных, то следует пользоваться формулой (5.20), в противном случае — формулой (5.19).

Знаменатели функций Р_i(s) одинаковы, поэтому целесообразно искать оригинал К_г(t), осуществив предварительно все возможные преобразования суммы слагаемых.

• Вычисление коэффициента готовности

Коэффициент готовности является финальной вероятностью пребывания системы в исправном состояний, поэтому его можно найти из (5.19), вычислив один из следующих пределов

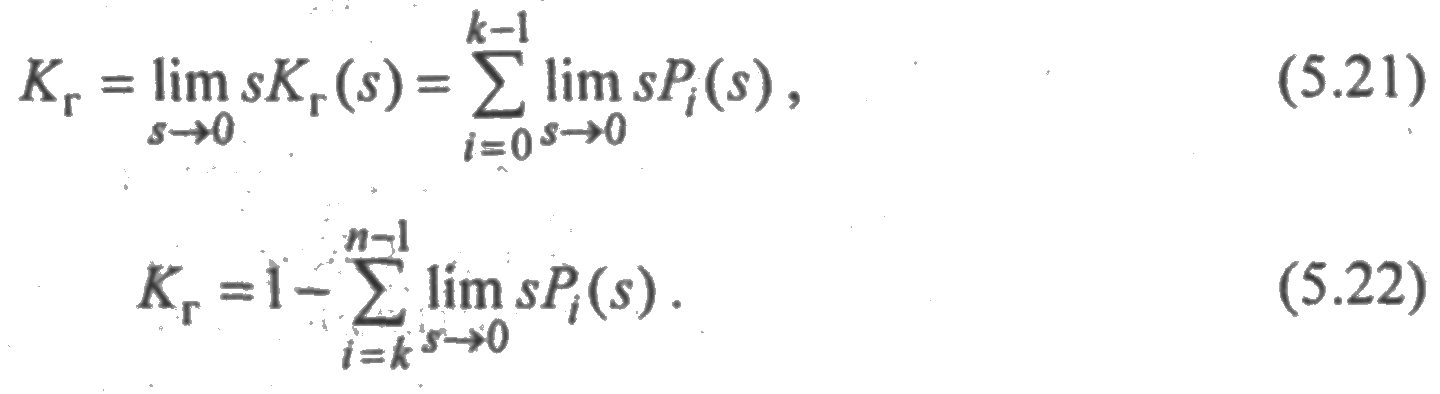
Наиболее просто можно вычислить коэффициент готовности для графа типа дерева непосредственно по графу состояний, если просуммировать выражение (5.17) по всем i, соответствующим исправным состояниям системы. В результате суммирования получим:

где п — общее число узлов графа;

k — число узлов графа, равных числу исправных состояний системы;

В_тi — произведение всех интенсивности переходов графа, которые встречаются при движении по стрелкам из крайних свободных состояний в состояние i по кратчайшему пути.

• Вычисление вероятности безотказной работы

Вероятность безотказной работы является вероятностью того, что восстанавливаемая система в течение времени t не попадет ни в одно из ее отказовых состояний. Поэтому искомая вероятность может быть вычислена по формуле

где P_i(t) — вероятность того, что система в течение времени t попадет в i-е исправное состояние;

k — число узлов графа, соответствующих числу исправных состояний системы.

Для вычисления P_i(t) необходимо все отказовые состояния считать поглощающими и запретить все переходы из этих состояний в предотказовые. Только после постановки экранов следует вычислять по графу состояний преобразования Лапласа функций P_i(t) в соответствии с методикой, изложенной в разд. 5.4.3.

Следует иметь в виду, что вероятность безотказной работы резервированной системы зависит от начальных условий ее функционирования. В задачах надежности вероятность безотказной работы обычно вычисляется в предположении, что при t = 0 все элементы системы исправны.

• Вычисление среднего времени безотказной работы

Среднее время безотказной работы системы вычисляется по формуле:

где Р_с(s) — преобразование Лапласа вероятности безотказной работы, вычисленной в предположении, что при t = 0 все элементы системы исправны.

Так как

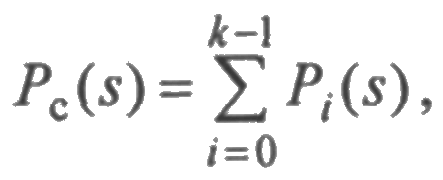
то

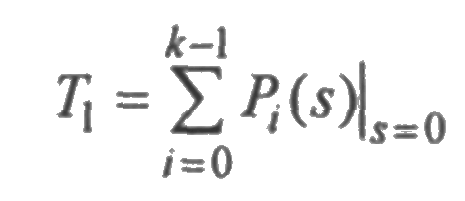
или

где T_i — среднее время пребывания системы в i-м исправном состоянии.

• Вычисление наработки на отказ

Наработка на отказ может быть вычислена по формуле

где Т_B — среднее время восстановления системы. Этой формулой целесообразно пользоваться тогда, когда среднее время восстановления системы известно из опыта или может быть легко вычислено. Тогда задача сводит­ся к определению К_г из графа состояний одним из описанных ранее способов.

При неизвестном Т_В следует использовать формулу:

При вычислениях по этой формуле необходимо определять по графу финальные вероятности пребывания системы во всех возможных состояниях. Формула является наиболее общей, т. к. позволяет вычислять Т при любом числе отказовых состояний и при любой дисциплине обслуживания [57].