5.4.2. Определение финальных вероятностей состояний системы

Финальные вероятности пребывания системы в i-м состоянии можно вычислить, воспользовавшись соотношением

Подставляя в это выражение вероятность P_i(s) из (5.13), получим:

Таким образом, для вычисления финальных вероятностей достаточно определить свободные коэффициенты полиномов Δ_i(s) и Δ(s) по приведенным выше правилам. Однако коэффициенты В_тi и А_п-1 можно получить значительно проще непосредственно из графа состояний, если предположить, что в графе отсутствуют переходы через состояния.

Вероятность Р_i является величиной безразмерной, поэтому каждое из слагаемых коэффициентов В_тi и А_п-1 имеет одно и то же число сомножителей, равное (n-1). Так как слагаемые не должны содержать сомножителей вида а_ij·а_ji, то для графа типа дерева в каждое из них должна входить только одна из этих интенсивностей перехода.

На основании сформулированных выше правил коэффициент В_тi не имеет интенсивностей переходов из 1-го состояния и содержит только такие члены, в которые входят произведения интенсивностей переходов из начального состояния в i-е по кратчайшему пути.

Все это позволяет сделать следующий вывод: коэффициент В_тi имеет только один член, который представляет собой произведение всех интенсивностей переходов из крайних свободных узлов графа в i-е состояние. Так как

а это означает, что коэффициент A_n-1 имеет столько членов, сколько узлов в графе состояний. Каждое из слагаемых равно соответствующему коэффициенту В_тi и определяется по сформулиро­ванному выше правилу определения коэффициента В_тi для i-го состояния.

Таким образом, финальную вероятность пребывания системы в /-м состоянии по графу типа дерева можно определить по формуле:

где п — число узлов графа, В_тi— произведение интенсивностей переходов из всех крайних свободных узлов в узел, соответствующий i-му состоянию системы, при перемещении по кратчайшему пути в направлении стрелок.

ПРИМЕР 5.20. Необходимо определить финальные вероятности пребывания системы во всех возможных состояниях, схема расчета надежности которой приведена на рис. 5.25. Восстанавливает систему одна бригада обслуживания.

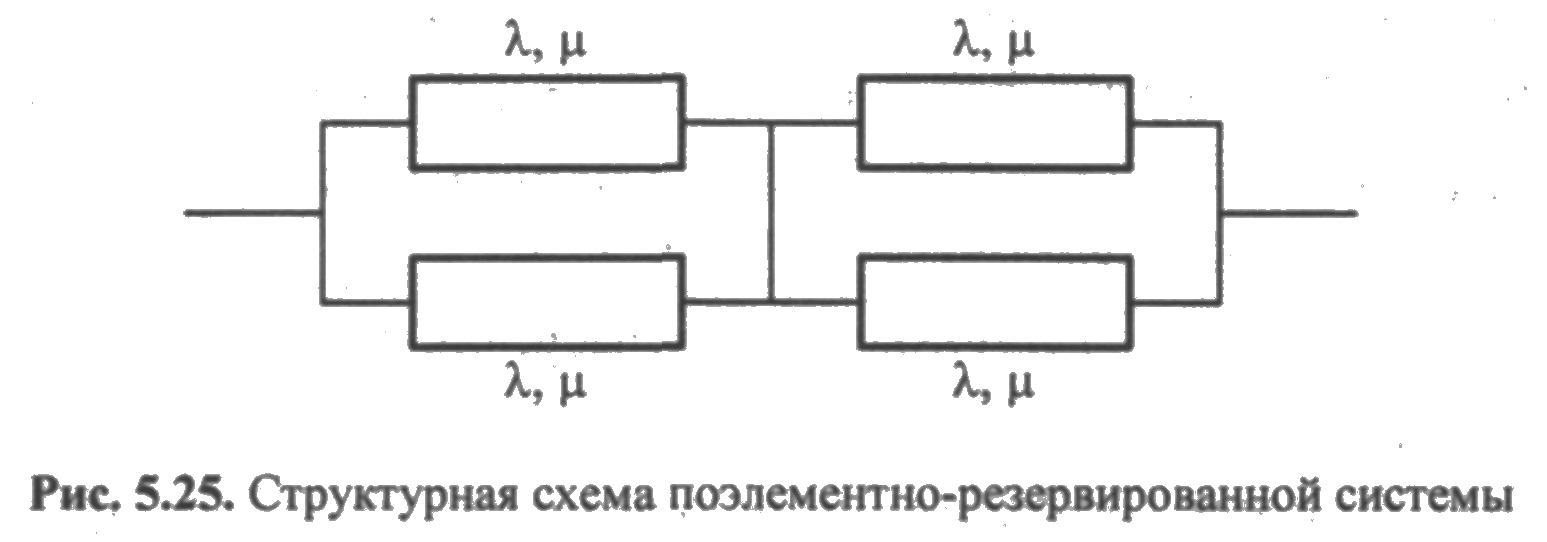
Решение. Из графа на рис. 5.26 видно, что система может находиться в пяти состояниях в соответствии с числом узлов графа, причем узлы 0, 2 и 4 являются крайними.

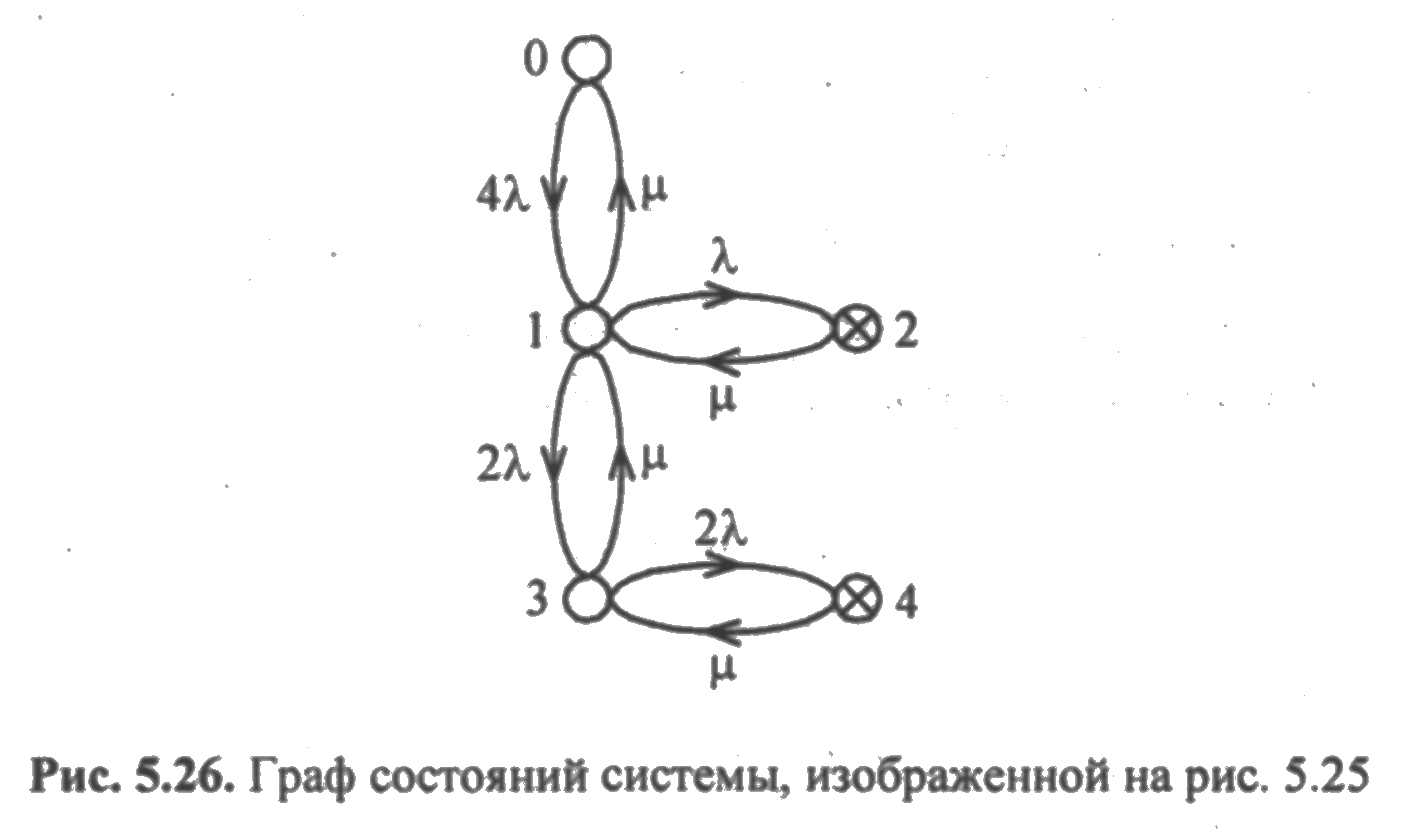
Перемещаясь из узлов 2 и 4 в узел 0 по направлению стрелок и перемножая все встречающиеся интенсивности переходов, получим:

Перемещаясь в узел 1 из крайних узлов 0,2 и 4, получим:

Аналогично,

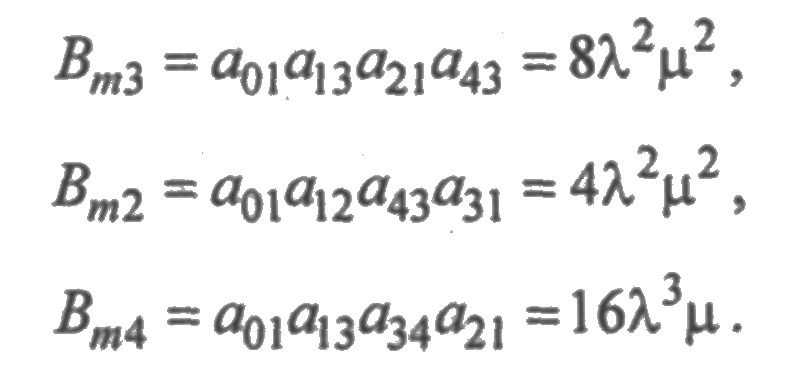
Тогда

и на основании (5.17) получим:

Из описания способа вычисления Р_i и приведенного примера видно, что определение финальных вероятностей по графу состояний значительно проще, чем путем решения уравнений функционирования системы.

5.4.3. Определение вероятности попадания системы в I-е состояние в течение времени t

Для определения преобразования Лапласа искомой вероятности по графу состояний достаточно во всех ветвях, выходящих из состояния i, поставить экраны и выполнить те же действия, что и в случае определения вероятности пребывания системы в i-м состоянии в данный момент времени.

Вероятность попадания системы в состояние i в течение времени t в преобразовании Лапласа может быть представлена в следующем виде:

где Δ(s) — главный определитель системы дифференциальных уравнений, записанной в преобразовании Лапласа; Δ_i(s)— частный определитель системы.

Выражения (5.18) и (5.13) принципиально отличаются друг от друга, несмотря на их внешнее сходство. Основные их отличия состоят в следующем:

• полином знаменателя выражения (5.13) не зависит от начальных условий и состояния i, в то время как коэффициенты полинома знаменателя выражения (5.18) зависят от состояния i, вероятность попадания в которое вычисляется по формуле (5.18);

• в отличие от (5.13),

Действительно, какова бы ни была структура системы и дисциплина обслуживания при t -→∞ (s→0), система обязательно попадет в состояние i.

ПРИМЕР 5.21. Необходимо определить вероятность попадания во все возможные состояния в течение времени t системы, схема расчета надежности которой и граф состояний приведены на рис. 5.23 и 5.24 соответственно. Условия функционирования системы те же, что и в примере 5.18.

Решение. Из графа видно, что система может находиться в четырех состояниях, поэтому п - 4, и на основании (5.18)

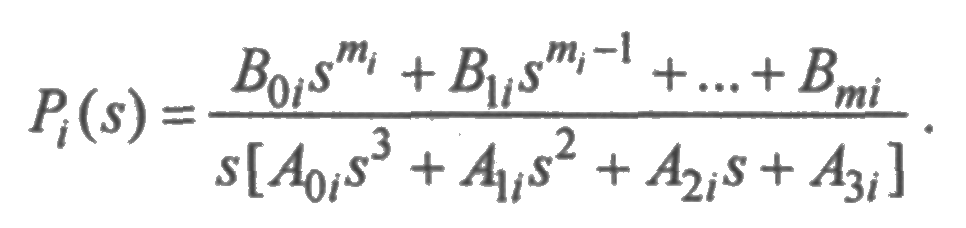
Сначала найдем вероятность попадания системы в состояние (0), для чего запретим переходы из состояния (0) в состояния (1) и (2), т.е. будем считать, что а₀₁ = а₀₂ = 0.

Вычисляя коэффициенты А_ji по описанной ранее методике, получим:

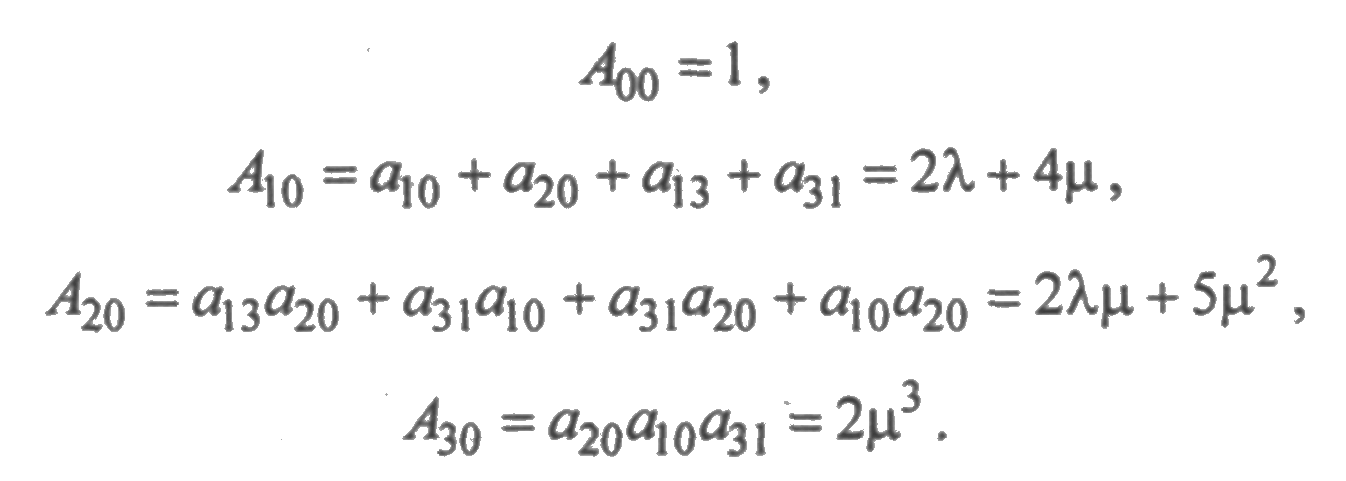
Степень полинома числителя на основании (5.14) будет иметь значение:

Тогда коэффициент В00 можно вычислить из коэффициента А₀₀, В₁₀ — из А₁₀, В₂₀ — из А₂₀, В₃₀ — из А₃₀. На основании сформулированного в разд. 5.4.1 правила коэффициенты В_j0, вычисляемые из соответствующих коэффициентов А_j0, не должны содержать в качестве сомножителей интенсивности переходов из состояния (0). Однако в данном случае коэффициенты А_j0 не содержат этих интенсивностей, т.к. состояние (0) является поглощающим. Тогда В₀₀ = А₀₀, В₁₀ = А₁₀, В₂₀ = А₂₀, В₃₀ = А₃₀ а значит Р₀(s) = 1/s, т.е. Р₀(t) = 1, что и следовало ожидать, т. к. по условию задачи при t = 0 система находится в состоянии (0) с вероятностью, равной единице.

Определим вероятность попадания системы в состояние (1), полагая, что это состояние является поглощающим и а₁₀ = а₁₃ = 0. При этом условии коэффициенты А_ji будут иметь значения:

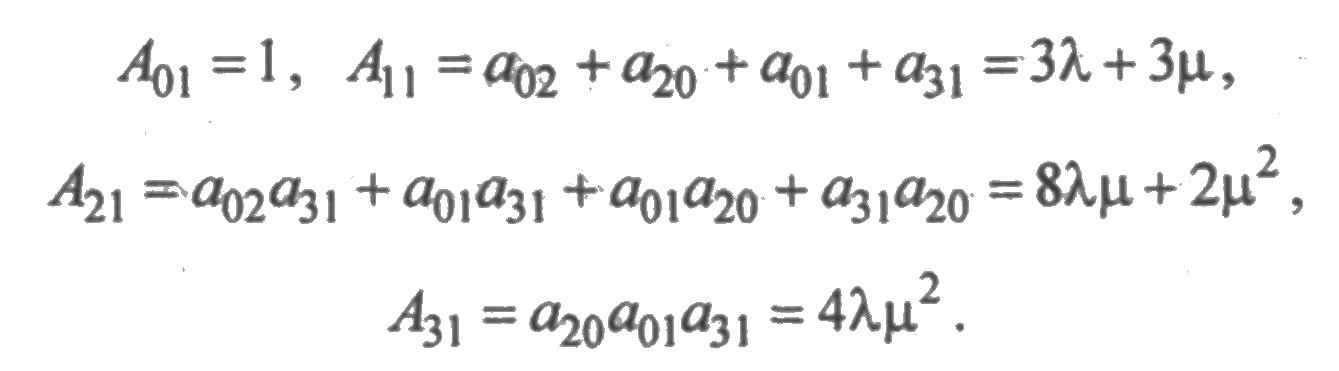
Степень полинома числителя будет:

Тогда Δi/(s)=В₀₁s²+B₁₁s+B₂₁, т.е. коэффициент В₀₁ вычисляется из коэффициента А₁₁, В₁₁ — из А₂₁, В₂₁ — из А₃₁. Коэффициенты В_ji должны содержать только те слагаемые, у которых в качестве сомножителя имеется интенсивность перехода из начального состояния (0) в состояние (1), т. е. а₀₁. Исключая из коэффициентов А_ji члены, не содержащие интенсивность а₀₁, получим:

Подставляя значения коэффициентов в полиномы числителя и знаменателя искомой вероятности, получим:

Вычисления P₁(s) можно было бы упростить, рассматривая граф рис. 5.24 без состояния (3). Действительно, если состояние (1) является поглощающим, то при начальных условиях Р₀(0) = 1, Р₁(0) = Р₂(0) = Р₃(0) = 0 система в состояние (3) перейти не может, а значит, это состояние является лишним.

Выполнив аналогичные вычисления, можно получить следующие выражения для вероятностей попадания системы в состояния (2) и (3):

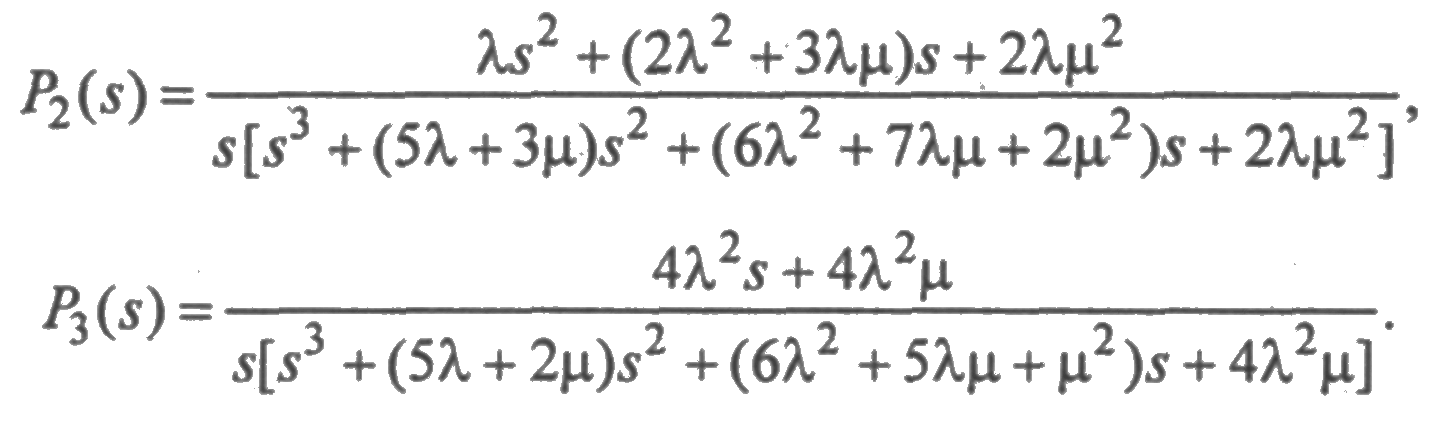
Из полученных выражений видно, что полиномы знаменателей P_i(s) различны, а для каждого состояния.