5.3.2. Метод кратчайших путей и минимальных сечений

Этот метод был рассмотрен ранее в разд. 5.2.3. Изложим его с позиции алгебры логики.

Функцию работоспособности можно описать с помощью кратчайших путей пешного функционирования системы и минимальных сечений ее отказа.

Кратчайшим путем называется минимальная конъюнкция работоспособных :стояний элементов, образующих работоспособную систему.

Минимальным сечением называется минимальная конъюнкция неработоспособных состояний элементов, образующих неработоспособное состояние системы.

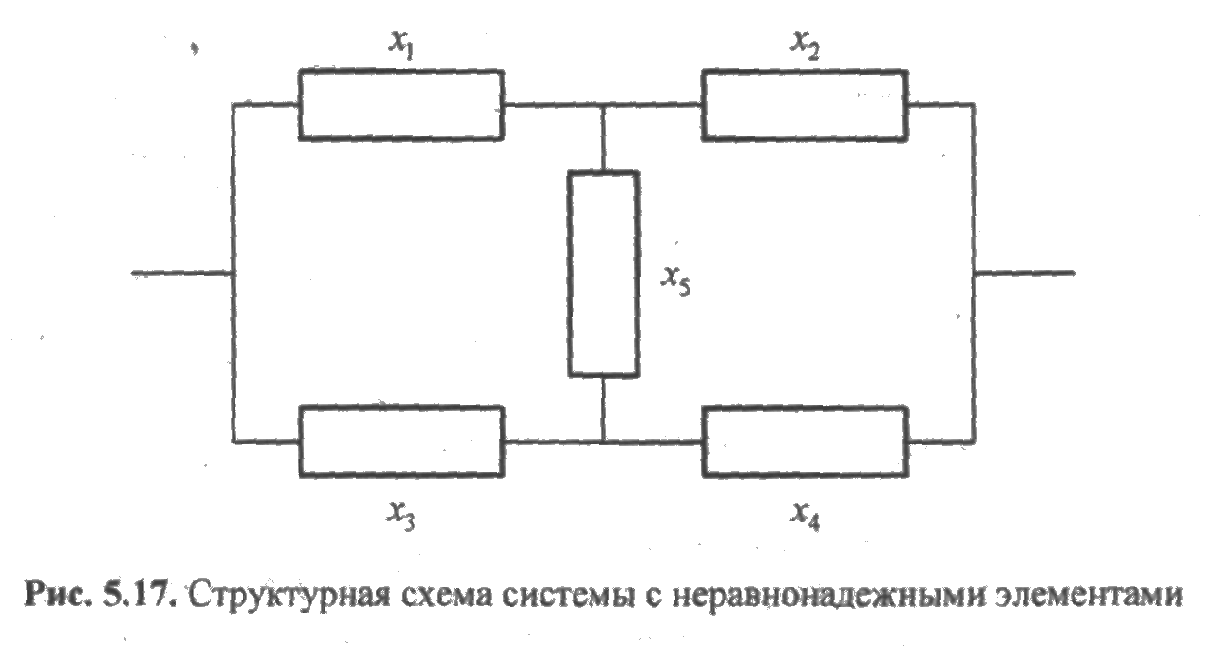
ПРИМЕР 5.13. Необходимо образовать функцию работоспособности системы структурная схема которой приведена на рис. 5.17, используя метод кратчайших путей и минимальных сечений.

Решение. В данном случае кратчайшими путями, образующими работоспособную систему, будут: х₁х₂, х₃х₄,, х₁х₅х₄, х₃х₅х₂. Тогда функция работоспособности запишется в виде следующей функции алгебры логики:

В соответствии с этой ФАЛ структурная схема системы рис. 5.17 может быть представлена структурной схемой рис. 5.18.

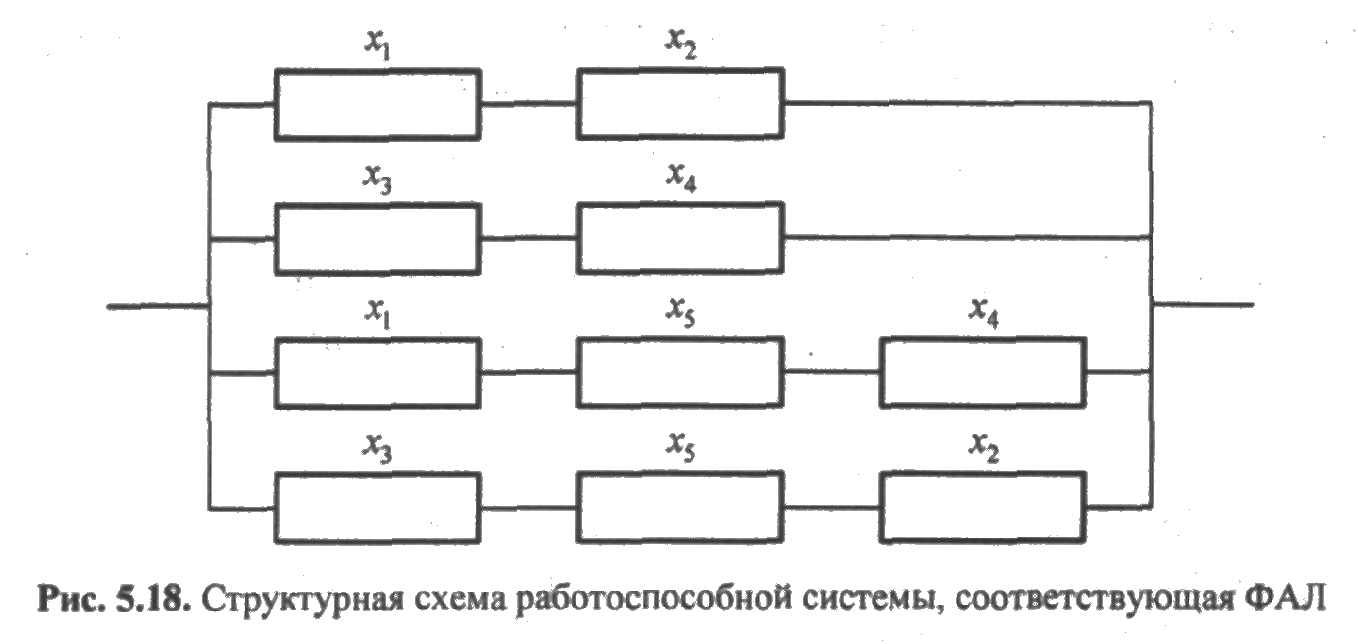
Минимальными сечениями, образующими неработоспособную систему, будут: х₁х₃, х₂х₄,, х₁х₅х₄, х₃х₅х₂. Тогда функция неработоспособности запишется в виде следующей функции алгебры логики:

В соответствии с этой ФАЛ структурная схема системы будет представлена в виде, показанном на рис. 5.19.

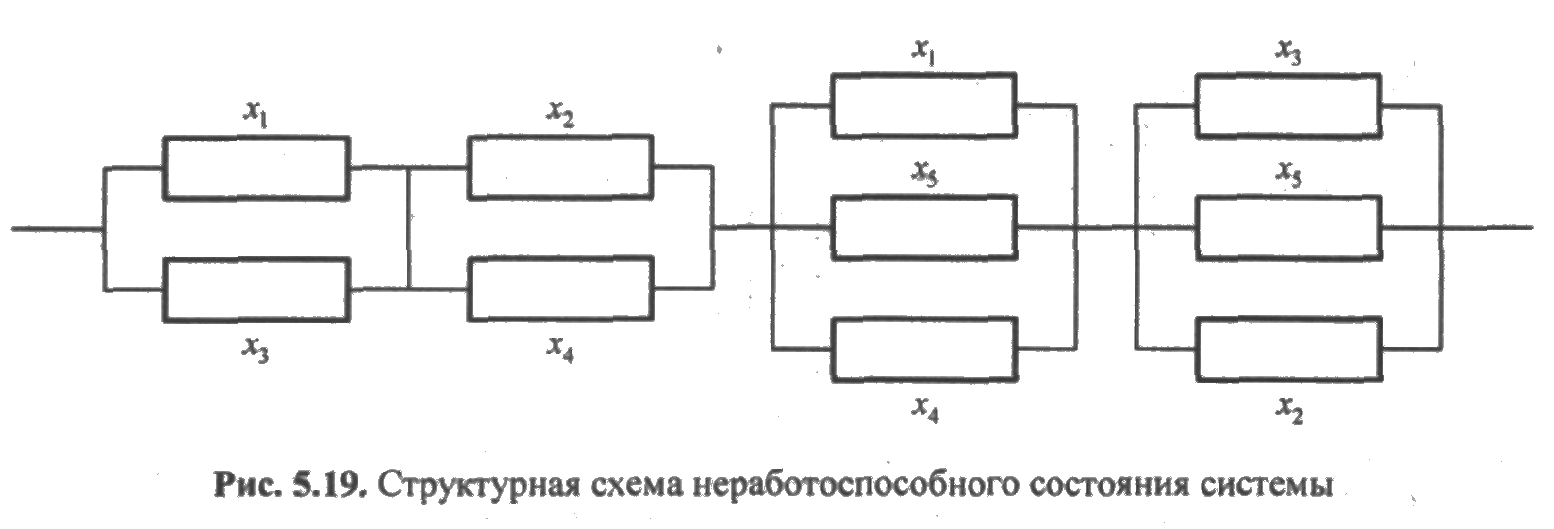
Следует иметь в виду, что структурные схемы рис. 5.18 и рис. 5.19 не являются схемами расчета надежности, а выражения для ФАЛ работоспособного и неработоспособного состояний не являются выражениями для определения вероятности безотказной работы и вероятности отказа:

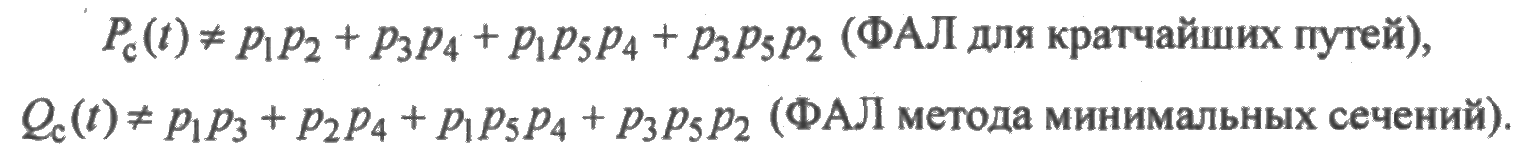
Основные достоинства ФАЛ в том, что они позволяют получить формально, не составляя таблицы истинности, СДНФ и СКНФ (совершенная конъюнктивная нормальная форма), которые дают возможность получить вероятность безотказной работы (вероятность отказа) системы путем подстановки в ФАЛ вместо логических переменных соответствующих значений вероятностей безотказной работы, заменив операции конъюнкции и дизъюнкции на алгебраические операции умножения и сложения.

Для получения СДНФ необходимо каждый дизъюнктивный член ФАЛ умножить на , где х_i — недостающий аргумент, и раскрыть скобки. Ответом будет СДНФ. Рассмотрим этот способ на примере.

ПРИМЕР 5.14. Необходимо определить вероятность безотказной работы системы, структурная схема которой приведена на рис. 5.17. Вероятности безотказной работы элементов равны р₁, р₂, р₃, р₄, р₅.

Решение. Воспользуемся методом кратчайших путей. Функция алгебры логики, полученная методом кратчайших путей, имеет вид:

Получим СДНФ системы. Для этого умножим дизъюнктивные члены на недостающие :

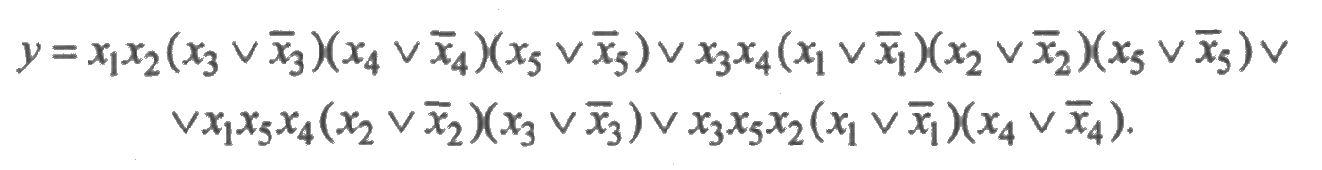
Раскрывая скобки и выполняя преобразования по правилам алгебры логики, получим СДНФ:

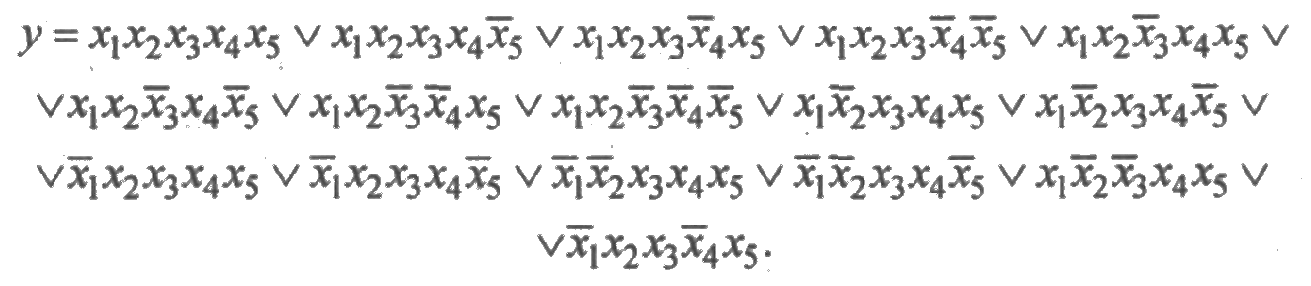
Подставляя в СДНФ вместо х₁, х₂, х₃, х₄, х₅ вероятности безотказной работы р₁, р₂, р₃, р₄, р₅ и используя соотношения q_i = 1–р_i, получим следующее выражение для вероятности безотказной работы системы.

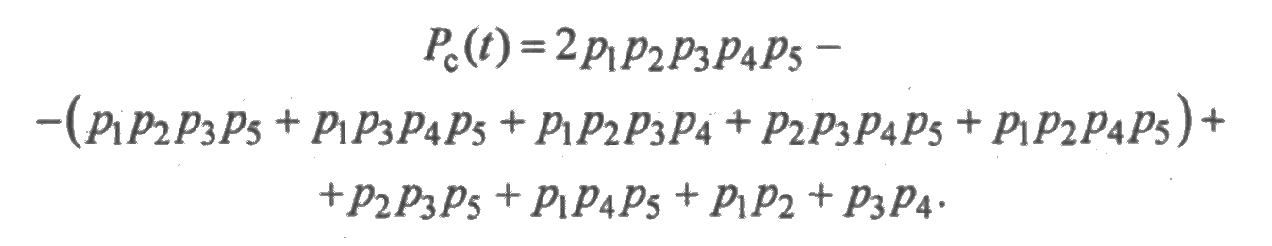
Из приведенного примера видно, что метод кратчайших путей освободил нас от определения благоприятных гипотез. Тот же результат можно получить, если воспользоваться методом минимальных сечений.