5.3. Логико-вероятностные методы анализа надежности

5.3.1. Сущность логико-вероятностных методов

Любой метод анализа надежности требует описания условий работоспособности системы. Такие условия могут быть сформулированы на основании:

- структурной схемы функционирования системы (схемы расчета надежности);

- словесного описания функционирования системы;

- граф-схемы;

- функции алгебры логики.

Логико-вероятностный метод анализа надежности позволяет формализовать определение и смысл благоприятных гипотез. Сущность этого метода состоит в следующем.

• Состояние каждого элемента кодируется нулем и единицей:

В функциях алгебры логики состояния элементов представляются в следующем виде:

• х_i — исправное состояние элемента, соответствующее коду 1;

• — отказовое состояние элемента, соответствующее коду 0.

• Записывается с помощью функций алгебры логики условие работоспособности системы через работоспособность (состояние) ее элементов. Полученная функция работоспособности системы является двоичной функцией двоичных, аргументов.

• Полученная ФАЛ преобразуется таким образом, чтобы в ней содержались члены, соответствующие благоприятным гипотезам исправной работы системы.

• В ФАЛ вместо двоичных переменных х_i и подставляются вероятности соответственно безотказной работы р_i и вероятности отказа q_i. Знаки конъюнкции и дизъюнкции заменяются алгебраическими умножением и сложением.

Полученное выражение и есть вероятность безотказной работы системы P_c(t).

Рассмотрим логико-вероятностный метод на примерах.

ПРИМЕР 5.10. Структурная схема системы представляет собой основное (последовательное) соединение элементов (рис. 5.14).

На структурной схеме х_i, i = 1, 2,..., п — состояние i-го элемента системы, кодируемое 0, если элемент находится в отказовом состоянии, и 1, если он исправный. В данном случае система исправна, если исправны все ее элементы. Тогда ФАЛ является конъюнкцией логических переменных, т.е. у=x₁,x₂,…..,х_п, представляющей собой совершенную дизъюнктивно нормальную форму системы.

Подставляя вместо логических переменных вероятности исправных состояний элементов и, заменяя конъюнкцию на алгебраическое умножение, получим:

ПРИМЕР 5.11. Структурная схема системы представляет собой дублированную систему с неравнонадежными, постоянно включенными подсистемами (рис. 5.15).

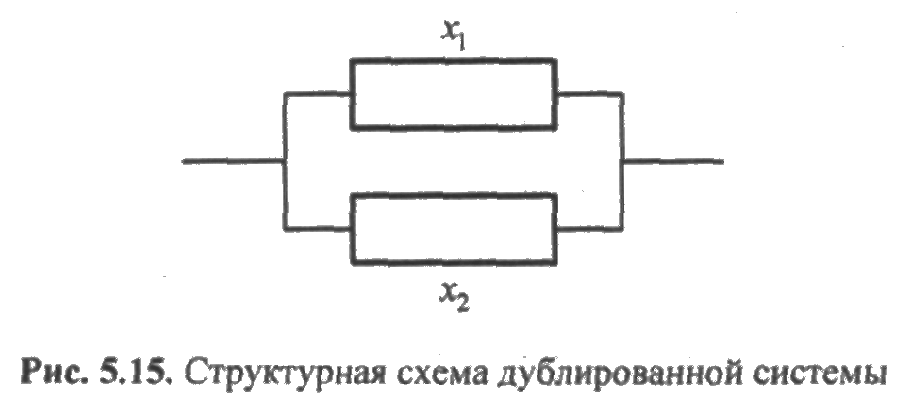
На рис. 5.15 х₁ и х₂ — состояния элементов системы. Составим таблицу истинности двух двоичных переменных (табл. 5.2).

В таблице 0 — отказовое состояние элемента, 1 — исправное состояние элемента. В данном случае система исправна, если исправны оба элемента (1,1) или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы описывается следующей функцией алгебры логики:

Эта функция является совершенной дизъюнктивной нормальной формой. Заменяя операции дизъюнкции и конъюнкции на алгебраические операции умножения и сложения, а логические переменные — на соответствующие вероятности состояния элементов, получим вероятность безотказной работы системы:

ПРИМЕР 5.12. Структурная схема системы имеет вид, показанный на рис. 5.16.

Составим таблицу истинности (табл. 53).

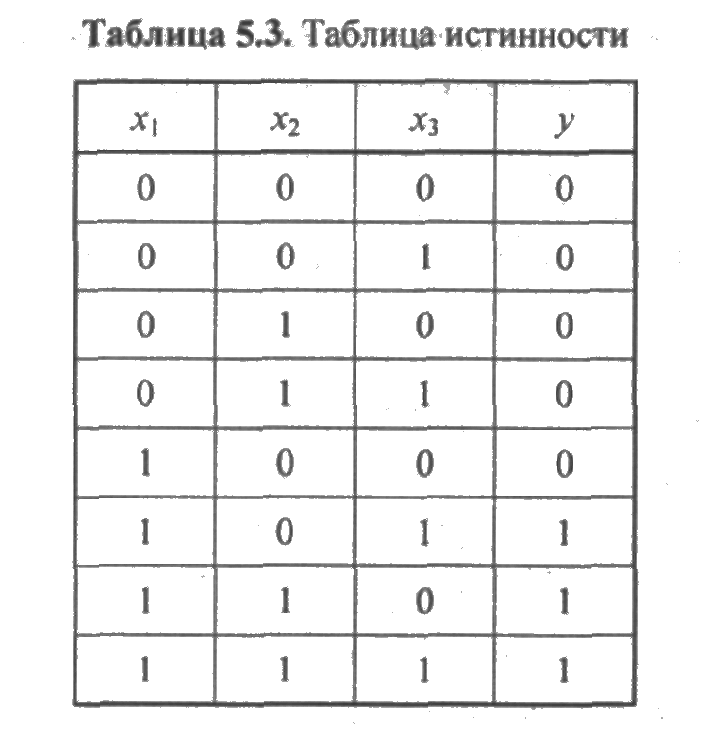
В данном примере система исправна, если исправны все ее элементы или исправным является элемент x_i и один из элементов дублированной пары (х₂, х₃). На основании таблицы истинности СДНФ будет иметь вид:

Подставляя вместо двоичных переменных соответствующие вероятности, а вместо конъюнкций и дизъюнкций — алгебраические умножение и сложение, получим вероятность безотказной работы системы:

Функцию алгебры логики можно представить в минимальной форме, если воспользоваться следующими преобразованиями:

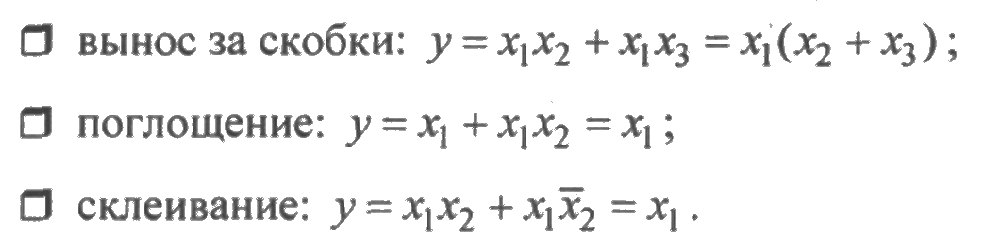
Операции поглощения и склеивания в алгебре не применимы. В связи с этим нельзя полученную ФАЛ минимизировать, а затем вместо логических переменных подставлять значения вероятностей. Вероятности состояний элементов следует подставлять в СДНФ, а упрощать по правилам алгебры.

Недостатком описанного метода является необходимость составления таблицы истинности, что требует перебора всех работоспособных состояний системы.