5.2.3. Метод минимальных путей и минимальных сечений

Введем два необходимых понятия.

Минимальный путь — такой набор элементов в структуре, при котором система исправна, если исправны все элементы этого набора; отказ любого из элементов ведет к отказу системы.

Минимальное сечение — такой набор элементов в структуре, при котором система неисправна, если неисправны все элементы этого набора; исключение любого элемента из набора переводит систему в исправное состояние.

У систем с произвольной структурой может быть несколько минимальных путей и минимальных сечений. Последовательное соединение из п элементов имеет один минимальный путь и п минимальных сечений, проходящих через каждый элемент. Параллельное соединение из п элементов имеет п минимальных путей, проходящих через каждый элемент, и одно минималь­ное сечение.

Пусть А₁,А₂,...,А_r — множество всех минимальных путей. Событие, состоящее в том, что все элементы пути А_i исправны, будем также обозначать А_i. Можно показать, что объединение событий А_i совпадает с множеством всех исправных состояний системы 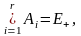и поэтому для вероятности безотказной работы справедливо равенство

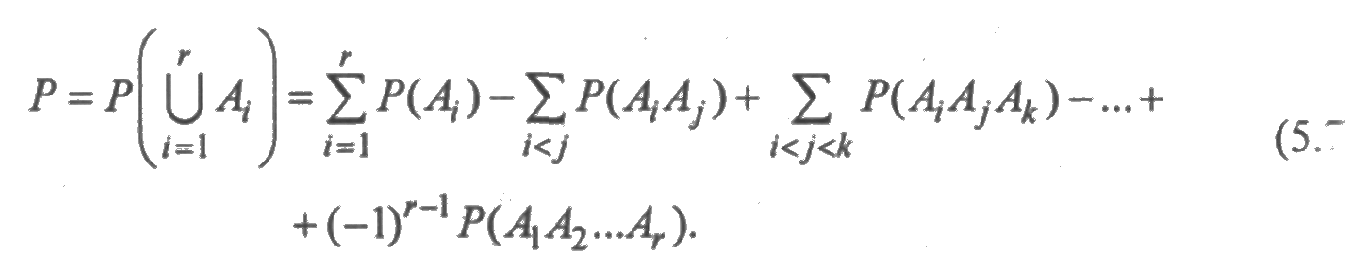
Пусть В₁,В₂,...,В_s — множество всех минимальных сечений. Событие, со стоящее в том, что все элементы сечения В_i неисправны, обозначим также через В_i. Можно показать, что объединение событий В_i совпадает с множеством всех отказовых состояний системы 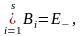и поэтому для вероятности отказа системы справедливо равенство

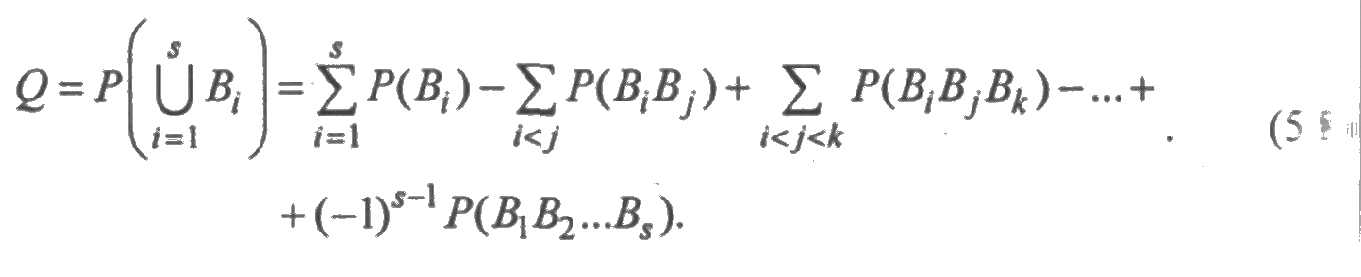
Каждая из вероятностей, стоящих в правой части (5.7) и (5.8), легко вычисляется. Однако если число путей или число сечений велико, то вычисление по этим формулам становится весьма сложной задачей.

ПРИМЕР 5.8. Методом минимальных путей и минимальных сечений требуется рассчитать надежность системы, структурная схема которой изображена на рис. 5.11,а.

Решение. Найдем минимальные пути: 1—3, 1—4, 2—3, 2—4. По формуле (5.7)

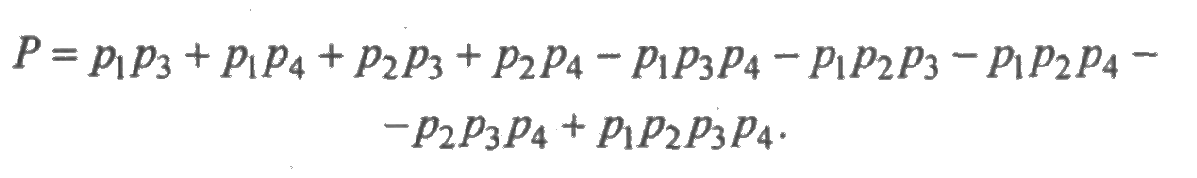
Найдем минимальные сечения: 1—2, 3—4. По формуле (5.8)

Нетрудно показать, что эти выражения равносильны выражению, полученному ранее:

Формулы (5.7) и (5.8), применяемые непосредственно для вычисления показателей надежности, все-таки достаточно громоздки и неудобны для расчетов. Тем не менее, на них базируются приближенные оценки вероятности безотказной работы.

Верхняя оценка вероятности безотказной работы определяется как вероятность безотказной работы параллельного соединения минимальных путей.

Верхняя оценка вероятности отказа системы определяется как вероятность отказа последовательного соединения минимальных сечений.

Отсюда получаются двусторонние оценки вероятности безотказной работы:

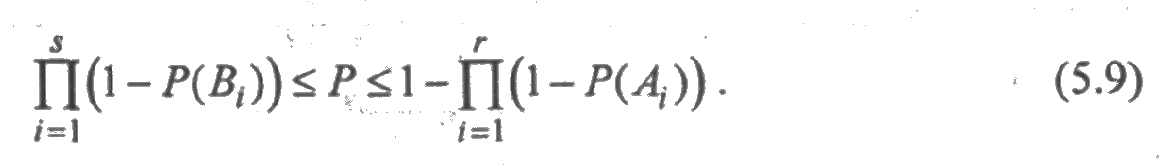
ПРИМЕР 5.9. Требуется оценить надежность мостиковой системы, структурная схема которой изображена на рис. 5.12.

Решение. Найдем все минимальные пут и соответствующие им вероятности:

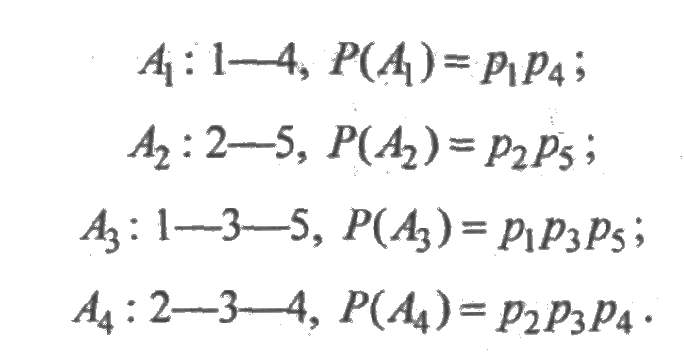
Найдем все минимальные сечения и соответствующие им вероятности:

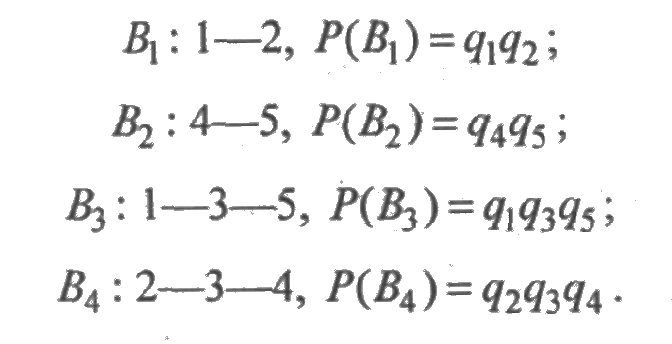
В соответствии с неравенствами (5.9) получим нижнюю и верхнюю оценки вероятности безотказной работы:

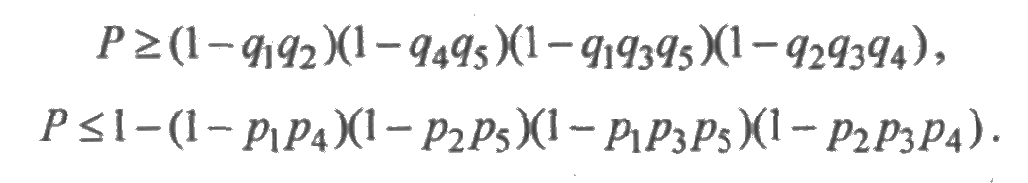
Если все элементы равнонадежны, то оценки приобретают вид:

Графическая иллюстрация этих оценок, когда р изменяется от 0 до 1 с шагом 0,1, приведена на рис. 5.13.