4.2.5. Правило составления системы интегральных уравнений

Для каждого состояния k ϵ Е интегральное уравнение составляется следующим образом. Определяются все состояния, из которых имеется одношаговый переход в состояние k . Пусть j — одно из таких состояний, и переход из j в k вызван отказом или восстановлением элемента с номером i₀ = i₀(k,l). Обозначим через Х_jk=(х₁,x₂, … , х_т) вектор, в котором композиты х₁ принимают два значения: х (переменная интегрирования) или 0. Если в состоянии k элемент с номером i работает или восстанавливается, то x_i = х. Если в состоянии k элемент с номером i находится в состоянии простоя, то х_i = 0.

Пусть для i-го элемента h_i есть плотность распределения времени безотказной работы f_i, если а_ik = s_i, или плотность распределения времени восстановления g_i, если а_ik = τ_i. Тогда справедливо уравнение:

Суммирование в правой части производится по всем состояниям j, из которых имеется непосредственный переход в состояние k. Произведение под знаком интеграла распространяется на все индексы i, для которых вектор А_k \ имеет "ненулевые" компоненты. Для начального состояния k₀ к правой части соответствующего интегрального уравнения (4.11) добавляется слагаемое

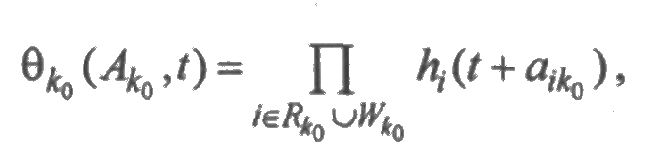
обусловленное началом функционирования системы.

В справедливости системы (4.11) можно убедиться путем подстановки в нее функций (4.8). Эта система описывает функционирование технической системы с произвольными законами распределения времени безотказной работы и времени восстановления элементов при заданных плотностях распределения вероятностей. Она содержит в себе всю вероятностную информацию о работе и восстановлении технической системы.

Решение системы (4.11) позволяет определить по формулам (4.9) и (4.10) соответственно вероятности пребывания системы во всех состояниях и параметры переходов из состояния в состояние. Далее по известным соотношениям рассчитываются любые характеристики надежности.

Описание с помощью системы интегральных уравнений является универсальным и при сделанных ранее допущениях может служить математической моделью функционирования любого сложного устройства с конечным или счетным множеством состояний. В частности, эта система пригодна для описания невосстанавливаемых и восстанавливаемых устройств при любом виде резервирования. Она может быть использована для описания стационарного и нестационарного режимов эксплуатации. Кроме того, в ряде случаев система (4.11) позволяет получить некоторые качественные свойства функционирования системы.

4.3. Общая модель функционирования системы в смысле надежности в терминах дифференциальных уравнений в частных производных

Система (4.11) может быть представлена также в виде эквивалентной системы дифференциальных уравнений в частных производных, каждое из которых является уравнением первого порядка. Для доказательства этого утверждения рассмотрим соотношение

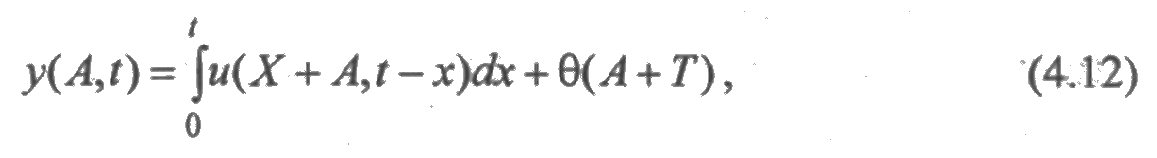
где А = (a₁, а₂,..., а_т), X = (х, х,..., х), Т = (t, t,..., t) — m-мерные векторы, у и и — дифференцируемые функции, зависящие от (т +1) аргумента, θ — дифференцируемая функция т аргументов. Применяя к обеим частям (4.12) оператор дифференцирования 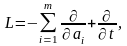получим:

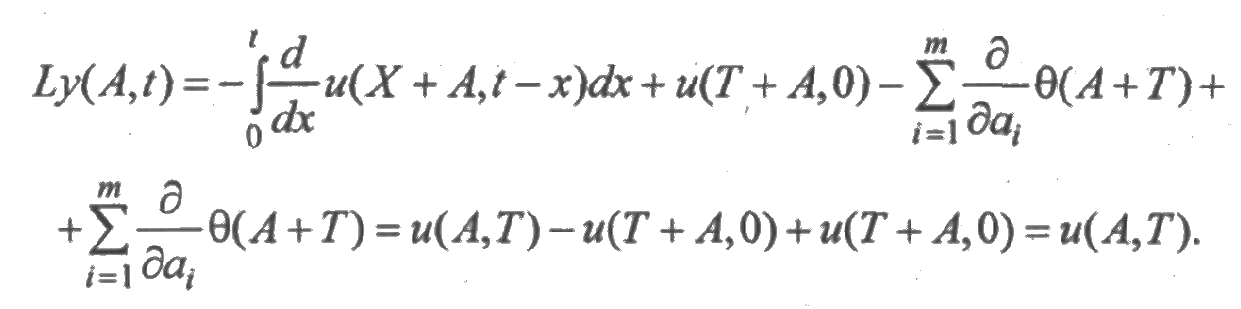
Таким образом, из равенства (4.12) следует, что

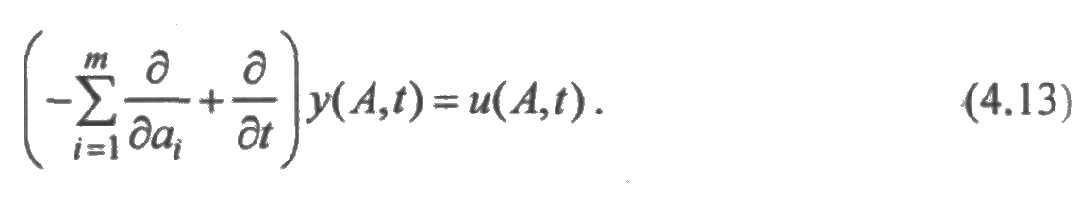
Очевидно также, что из (4.12) при t = 0 определяется начальное условие:

Верно и обратное. Из соотношений (4.13) и (4.14) следует (4.12).

Действительно, для этого достаточно от обеих частей равенства (4.13) вычислить криволинейный интеграл вдоль прямой, определяемой параметрическими уравнениями:

В результате будем иметь

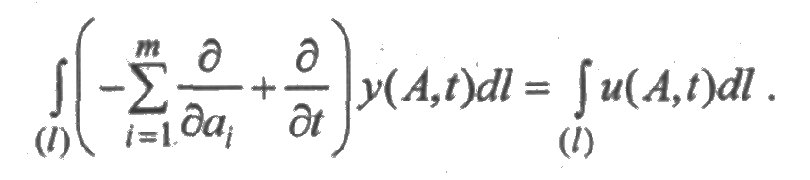
Произведя замену переменных, получим

или

Отсюда следует, что

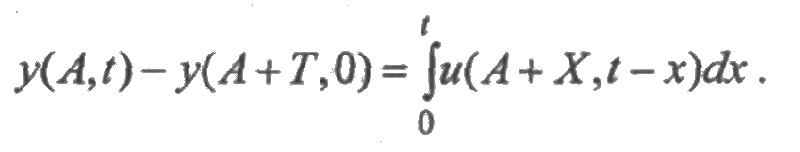
Используя начальное условие (4.14), получим (4.12). Из равносильности соотношений (4.12) и (4.13)—(4.14) следует эквивалентность системы интегральных уравнений (4.11) и следующей системы дифференциальных уравнений:

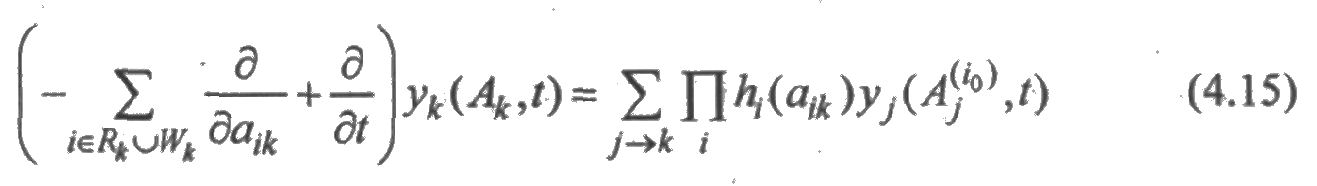
с дополнительными начальными условиями

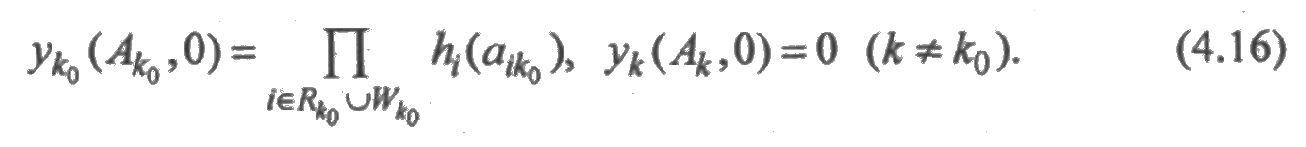
Произведение в правой части (4.15) распространяется на те множества индексов i, что и в (4.11), а суммирование производится по всем номерам состояний j, из которых существует одношаговый переход в состояние k.

ПРИМЕР 4.5. Составить систему интегральных и дифференциальных уравнений для описания функционирования основного соединения 3-х элементов из разд. 4.2.3.

Решение. Поскольку устройство имеет 6 возможных состояний, то неизвестными в системах уравнений являются 6 функций, аргументами которых служат столбцы матрицы состояний S и время t: y₀(s₁,s₂,s₃,t), y₁(τ₁,s_2’,s_3’,t), y₂(s_1’,τ₂,s_3’,t), y₃(s₁,s₂,τ_3’,t), y₃₁(τ₁,s_2’,τ_3’,t), y₃₂(s_1’,τ₂,τ_3’,t). Система инте­гральных уравнений составляется в соответствии с общей методикой по формуле (4.11), считая, что в момент времени t = 0 все элементы исправны:

Система дифференциальных уравнений составляется исходя из равенств (4.15):

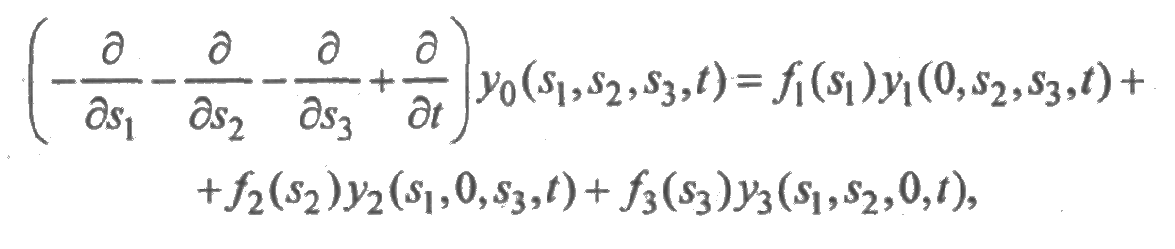
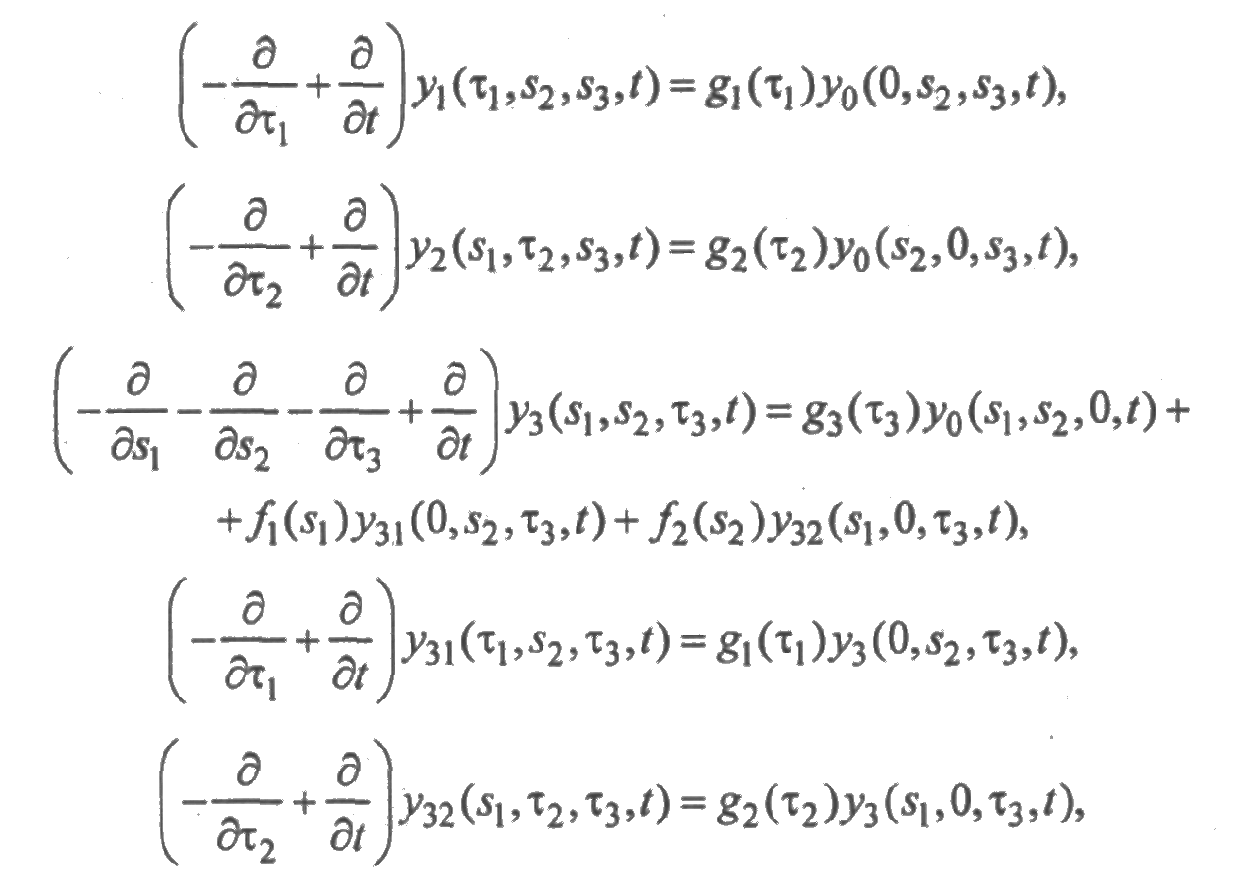
а начальные условия — исходя из равенств (4.16):

Остальные функции при t = 0 равны нулю.