4.2.4. Выражения для вероятностей состояний и параметров переходов между состояниями

Функционирование технической системы с произвольными законами распределения элементов может быть описано системой интегральных уравнений или эквивалентной системой дифференциальных уравнений в частных производных. Эти системы уравнений строятся непосредственно по матрице состояний S и матрице переходов Р.

Сначала получим явные соотношения для вероятностей состояний системы р_k(t) и параметров перехода из состояния в состояние ω_kl(t), k,l ϵ Е. Пусть k₀ — начальное состояние процесса функционирования технической системы. Обозначим через Г^(r)_k0,k множество всех путей графа состояний длины r с началом в узле k₀ и концом в узле k. Двигаясь по пути γ ϵ Г^(r)_k0,k , можно попасть из состояния k₀ в состояние k за r шагов (некоторые ветви при этом могут повторяться). Напомним, что за один шаг принимается переход, обусловленный или отказом, или восстановлением какого-либо одного элемента системы. Предположим, что путь γ проходит через состояния с номерами k₀,k₁,k₂,:,k_r=k. Обозначим через x_j время пребывания системы в состоянии k_j, а через x = (x₀, x₁,…., x_r) — вектор с компонентами x_j.

Рассмотрим изменение состояний i-го элемента на пути γ и определим функции 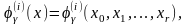характеризующие плотность распределения вероятностей пребывания i-го элемента в состоянии k_j в течение времени x_j, j = 0,1,2,..., r. Каждому узлу k_j отвечает значение i-й компоненты 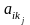, равной одной из величин: s,s',τ,τ',OR,OW, при этом указанные величины чередуются в следующем порядке: OR (очередь на работу), s или s' (работа или прерывание работы), OW (очередь на восстановление), τ или τ' (восстановление или прерывание восстановления). Некоторые из приведенных величин могут быть опущены. Множество индексов {0,1,2,...,r} представимо в виде объединения непересекающихся подмножеств, состоящих из индексов, следующих в порядке возрастания:

где

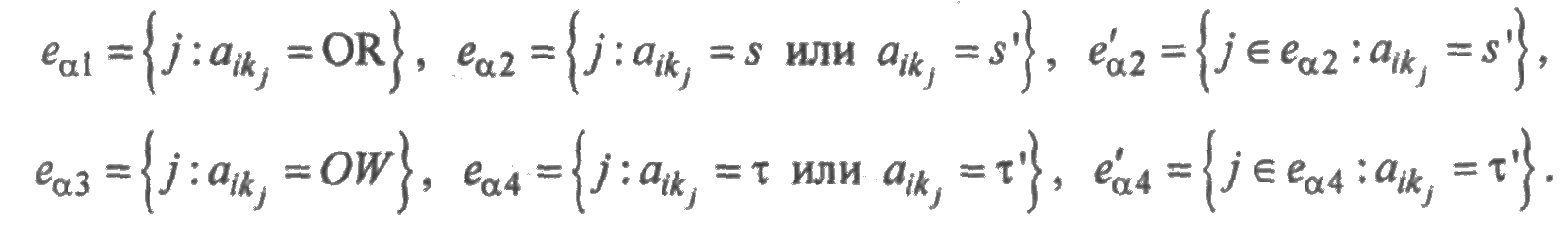
Тогда функция 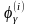определяется равенством

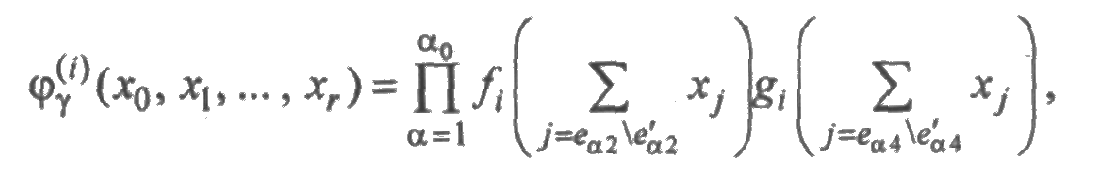
где f_i(t) и g_i(t) — плотности распределения времени безотказной работы и времени восстановления i-го элемента. С точностью до бесконечно малой величины Δх₀Δx_1….Δx_r функция равна, очевидно, мгновенной вероятности того, что i-й элемент пребывает в состоянии k_j время x_j, j=0,1,2,…,r.

Предположим, что последнее состояние k = k_r является состоянием работы или восстановления i-го элемента. Тогда имеет смысл говорить о мгновенной вероятности того, что i-й элемент в каждом состоянии k_j, кроме последнего, пребывает время x_j, а в последнем состоянии— время, не меньше x_r.

Совершенно ясно, что эта вероятность равна

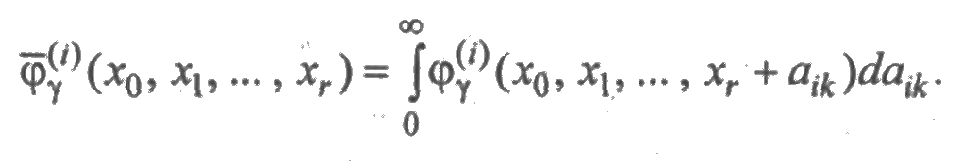
ПРИМЕР 4.4. Пусть i-й элемент системы пребывает в состояниях s, τ, OR, s, τ, τ', τ, s, как показано на временной диаграмме (рис. 4.5). Требуется составить выражения для функций и ,

Решение. На рис. 4.5 x₀, х₁, х₂, х₃, х₄, х₅, х₆, х₇ — времена пребывания 1-го элемента в соответствующих состояниях. Из диаграммы следует, что

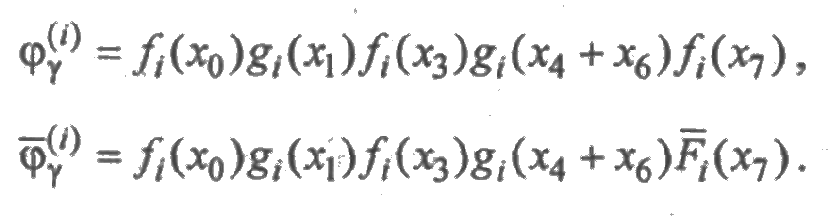
Вероятность р_k(t) пребывания системы в момент временя t в состоянии k находится по формуле полной вероятности. Пусть H_γ(t) — событие, состоящее в том, что в момент t система достигла состояния k, двигаясь из начального состояния k₀ по пути γ ϵ 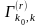. Вероятность этого события равна

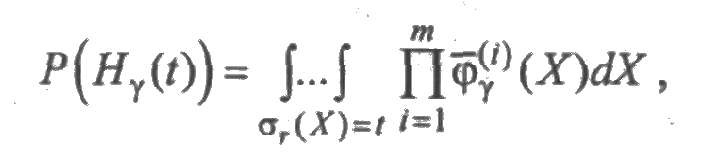
где σ_r(X) = t обозначает гиперплоскость 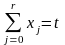в (r + 1)-мерном евклидовом пространстве. Искомая вероятность равна сумме вероятностей событий Н_γ(t), вычисленной по всем путям γ, ведущим из состояния k₀ в состояние k, т. е.

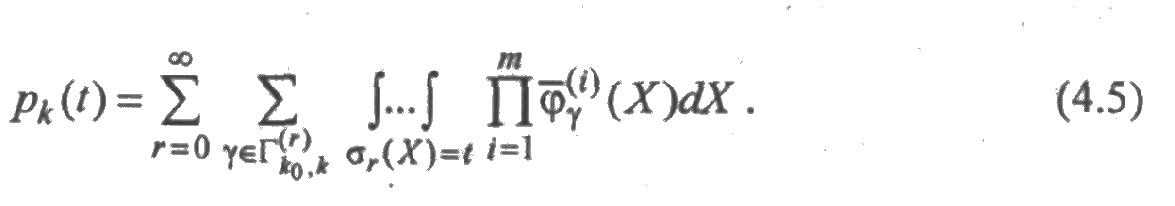
Рассмотрим переход системы из состояния k в состояние l. Пусть этот переход вызван отказом или восстановлением элемента с номером i₀=i₀(k,l). Параметр перехода ω_k,l(t) представляет собой мгновенную вероятность перехода в момент t из состояния k в состояние l, отнесенную к единице времени, т. е.

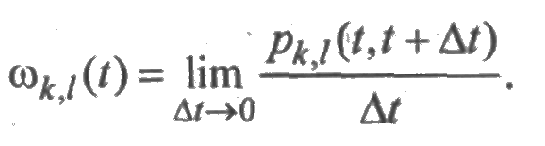
Поэтому для получения параметра перехода необходимо в формуле (4.5) все функции при i≠i₀ оставить без изменения, а функцию 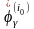— заменить на выражение

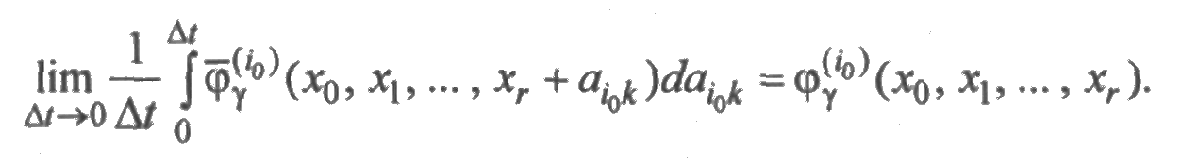
Таким образом,

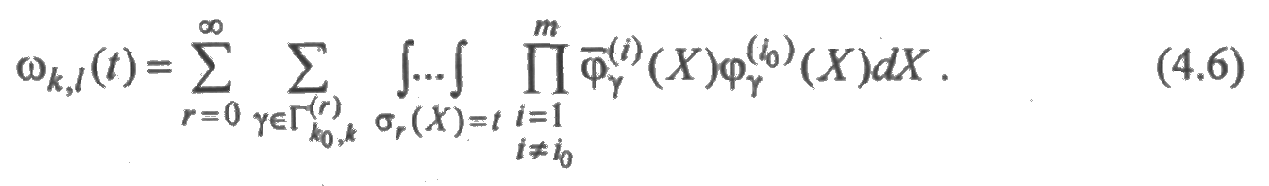
Выражения (4.5) и (4.6) похожи по форме записи, поэтому их можно рассматривать совместно. С этой целью обозначим через Y_k{А_k,t) = Y_k(a_1k, а_2k,, ..., а_тk, t) вероятность пребывания системы в момент времени t в состоянии k в предположении, что после момента t i-й элемент системы сохранит свое состояние работоспособности или восстановления в течение времени а_1k (i = 1, 2, ..., т). Предположим, что функции Y_k имеют частные производные по всем переменным вида s иτ. Обозначим через y_k смешанную производную по этим переменным порядка α=|R_k ᴗ W_k| со знаком "+" или "-", определяемую формулой

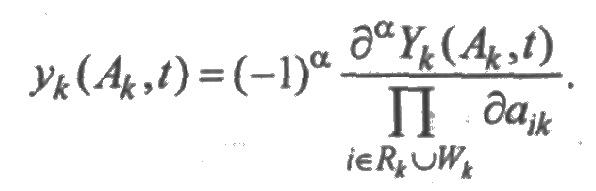
Функции у_k представляют собой плотности распределения вероятностей и являются неизвестными в системе интегральных уравнений.

Поскольку

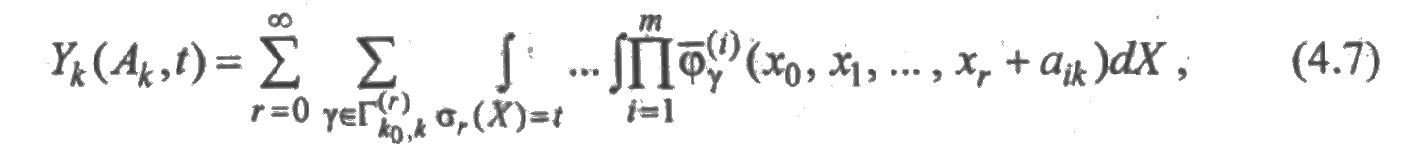
то

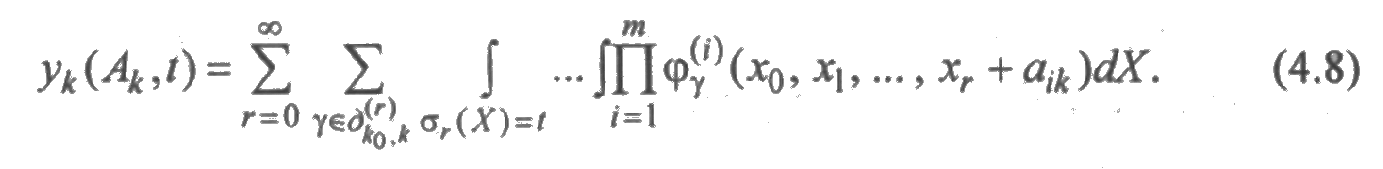
Вероятности состояний и параметры переходов находятся по функциям у_k с помощью единообразных соотношений. Действительно, как следует из (4.8), а также из (4.5) и (4.6), имеют место равенства:

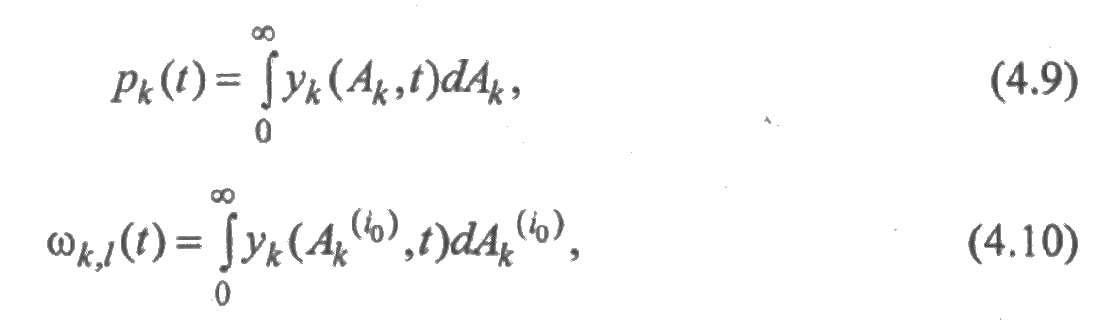
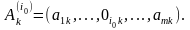где i₀ = i₀(k,l) — номер элемента, вызвавшего переход k→l, а вектор ⁾ получается из А_k, если положить в нем компоненту с номером i₀ равной нулю, т.е. Интегрирование в (4.9) и (4.10) распространяется на все "ненулевые" значения переменных a_ik. В некоторых случаях удобно вычислять неизвестные функции прямо через вероятности Y_k в соответствии с формулами:

где 0 = (0, 0,..., 0) — нулевой вектор. Отсюда, в частности, следует, что при малых значениях параметров а_ik справедливо разложение

Суммирование в правой части распространяется на все состояния k и l, между которыми имеются переходы k→l.