3.3.4. Критичное влияние произвольных распределений отказов и восстановлений на нестационарные показатели надежности

Практические задачи, возникающие в теории надежности, показывают важность расчета и анализа нестационарных характеристик, которые часто не принимаются во внимание, хотя, как показывают вычислительные эксперименты, продолжительность переходного процесса может быть довольно большой. Более того, существуют системы, стационарное состояние которых вообще не наступает.

Пусть f(t) и g(t) — плотности распределения времени безотказной работы и времени восстановления элемента. Как было показано в разд. 2.6.1, функция готовности системы удовлетворяет уравнению

где функция ω_в, находится из уравнения

Численное решение этих уравнений для многих распределений не представляет затруднений. Получим аналитические выражения функции готовности для некоторых часто встречающихся распределений.

В преобразовании Лапласа выражение функции готовности имеет вид:

Случай 1. Если законы распределения экспоненциальные с параметрами λ и μ, то, как известно,

Случай 2. Закон распределения времени безотказной работы экспоненциальный, а времени восстановления — Эрланга 2-го порядка с параметром μ. Из (3.1) следует, что

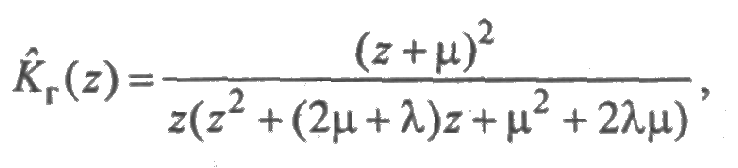
и функция готовности находится в явном виде:

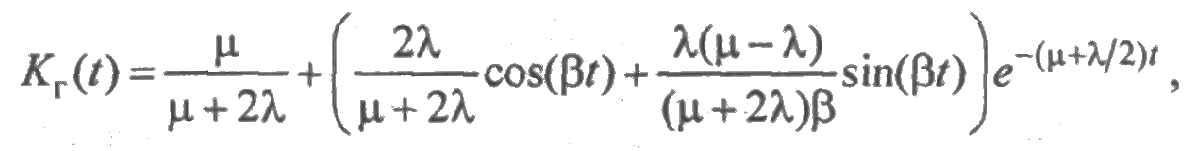
где 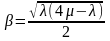при μ >λ/4. Точки экстремума b_к получаются в результате решения уравнения: 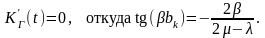Тем самым

и функция K_г(t) имеет бесконечное число точек экстремума, а это соответствует колебательному процессу. Для значения b₁, имеем

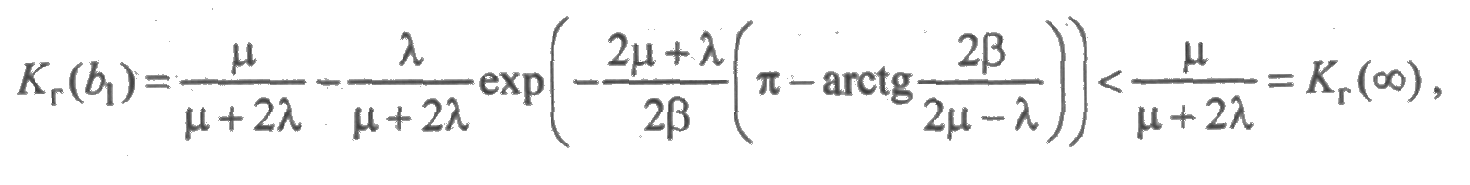
т. е. b₁ — точка минимума, в которой график функции готовности лежит ниже стационарного значения К_г. Значения a_k, в которых график функции готовности пересекает линию К_г(t) = К_г, определяются из уравнения

Это доказывает, что для произвольных распределений могут наблюдаться провалы функции готовности ниже ее стационарного значения. Графики функций готовности для 1-го и 2-го случаев приведены на рис. 3.4.

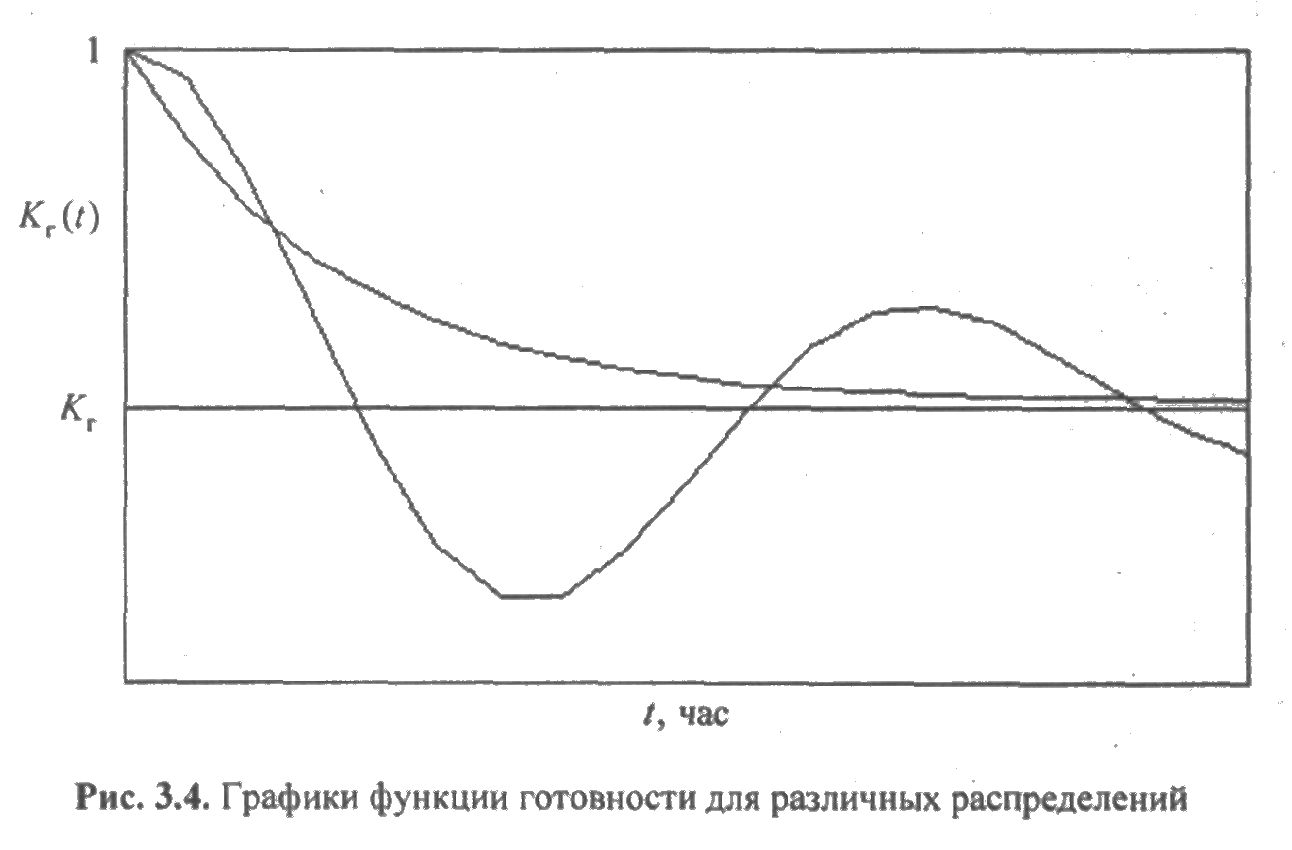
Для равномерного распределения с параметрами а и b преобразование Лапласа функции готовности имеет вид:

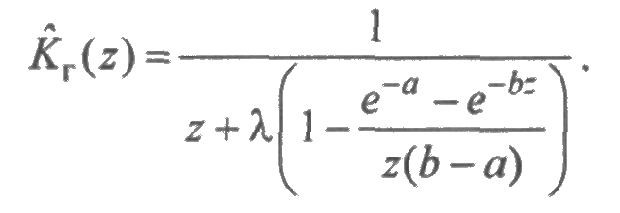
В этом случае в явном виде найти функцию готовности не удается. Тем не менее, расчеты, выполненные на ЭВМ, показывают достаточную близость функций готовности для равномерного распределения и распределения Эрланга. Таким образом, в отличие от экспоненциального случая, когда функция готовности всегда является монотонно убывающей, в общем случае функция готовности часто имеет колебательный характер. Поэтому может оказаться, что готовность системы для небольшого времени эксплуатации меньше, чем при ее длительной эксплуатации. Этот факт часто игнорируется на практике, что может привести к нежелательным результатам.

Можно показать, что с уменьшением дисперсии времен безотказной работы элементов усиливается колебательный характер функции К_г(t) и значительно увеличивается время наступления стационарного режима системы.

Случай 3. Законы распределения вырожденные со средними Т и Т_в, соответственно. В этом случае из (3.1) получим:

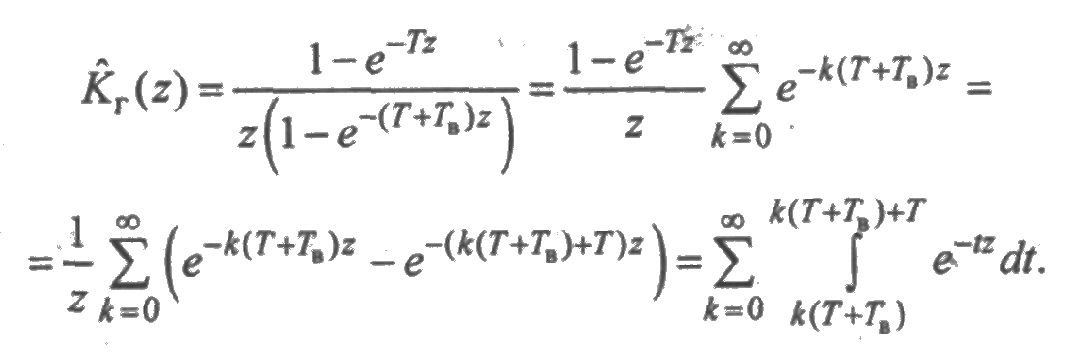
Из этого выражения следует, что функция К_г(t) тождественно равна единице на интервалах [k(Т + T_в), k(Т + T_в) + Т], k = 0,1, 2,..., и равна нулю вне этих интервалов, т.е.

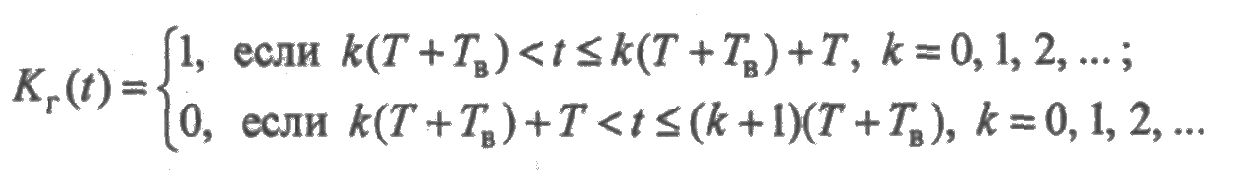
График функции готовности приведен на рис. 3.5.

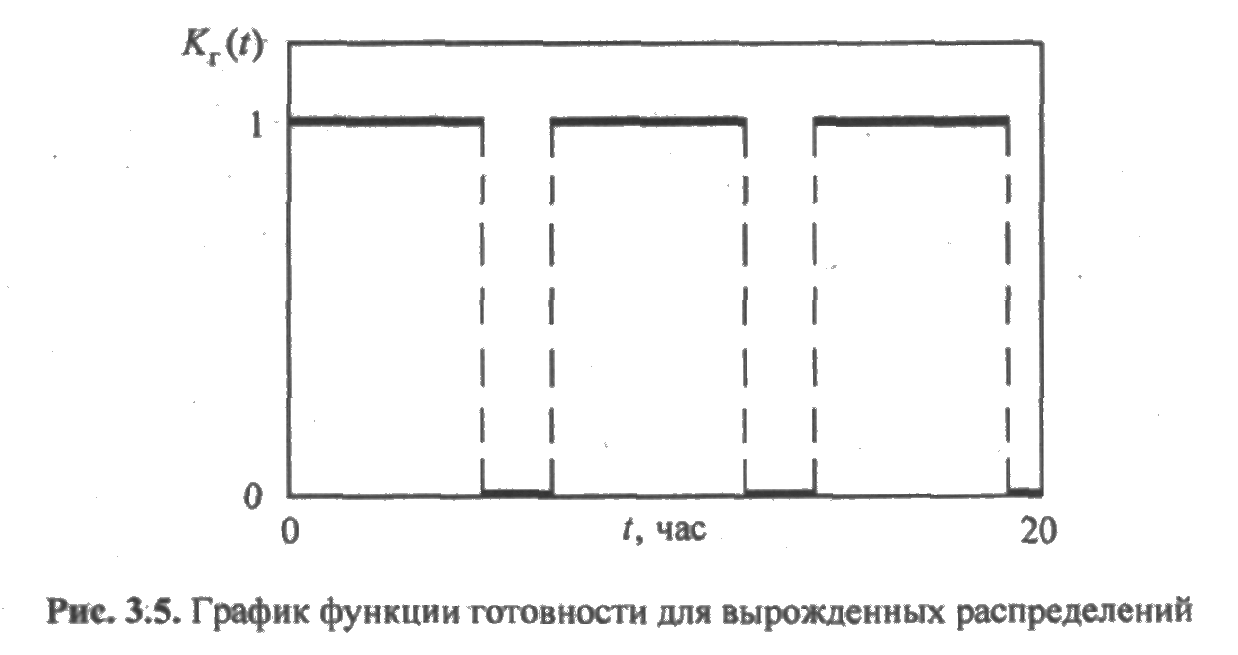
Стационарный режим здесь вообще не наступает, и коэффициент готовности не существует.