3.3.3. Зависимость показателей надежности от законов распределения и дисциплины восстановления элементов

В теории надежности важное место отводится нахождению простых приближенных расчетных формул для показателей надежности. В то же время эти формулы должны иметь достаточно высокую точность, удовлетворяющую инженера-практика. Как показывают исследования, даже в случае простейших резервированных систем не удаётся найти простых аналитических соотношений для вычисления показателей надежности с требуемой точностью. Исключение составляют некоторые системы специального вида, показатели надежности которых зависят только от математических ожиданий времени безотказной работы и времени восстановления элементов и не зависят от законов распределения. Так бывает, например, в следующих случаях:

- элементы системы независимы по отказам и восстановлению (параллельное соединение с неограниченным восстановлением);

- при вычислении стационарных показателей надежности, когда отсутствует очередь на работу исправных элементов и очередь на восстановление отказавших элементов системы.

Однако при вычислении показателей надежности, как правило, недостаточно знать лишь первые моменты соответствующих распределений. Если даже предположить, что среднее время восстановления элементов значительно меньше среднего времени их исправной работы, то и в этом случае существующие расчетные формулы дают весьма грубые приближения к истинным значениям показателей надежности. При надлежащем выборе законов распределения относительная погрешность может быть очень высокой и даже неограниченной. Кроме того, эти формулы не учитывают приоритета обслуживания отказавших элементов. Как известно, для экспоненциальных распределений дисциплина восстановления элементов незначительно влияет на показатели надежности всей системы, особенно если ее функционирование протекает при дополнительном условии "быстрого" восстановления. Однако если законы распределения неэкспоненциальны, то дисциплина восстановления может оказать существенное влияние на надежность системы. В этом можно убедиться на примерах некоторых резервированных систем.

ПРИМЕР 3.1. Дано: восстанавливаемая дублированная система, составленная из равнонадежных элементов с ограниченным восстановлением. Оценить влияние дисциплины восстановления элементов на среднюю наработку на отказ системы.

Решение. Предположим, что время безотказной работы элементов экспоненциальное с параметром λ, а время восстановления имеет произвольное распределение с плотностью g(t)/ В гл. 7 будет показано, что средняя наработка на отказ для прямого, обратного и назначенного приоритетов выражается формулами:

Здесь и далее — преобразование Лапласа (см. разд. 2.5) функции g(t), T_в — среднее время восстановления элементов. Предположим, что g(t)=cμe^-μt + (1-c)νe^-νt и имеет место "быстрое" восстановление элементов, например: Т = 100 час, Т_в=1 час. Тогда λ = 0,01 час^-1, Путем простых преобразований легко показать, что Т^(пр) →∞, если μ→0, ν→∞, тогда как Т^(обр)=5100 час. Например, полагая μ = 0,001 час^-1, ν = 10, получим Т^(пр) = 27 577 час, Т^(наз) = 8565 час. Таким образом, средняя наработка на отказ системы существенно зависит от приоритета обслуживания элементов. Сопоставим полученные результаты с асимптотической формулой 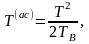справедливой при условии "быстрого" восстановления элементов и любой дисциплины восстановления. Видим, что Т^(ас) = 5000 час и существенно отличается от ее точного значения. Следовательно, простота асимптотических формул не может служить основанием для возможности их применения при оценке надежности резервированных систем.

ПРИМЕР 3.2. Дано: восстанавливаемая дублированная система из равнонадежных элементов, обслуживаемая одним ремонтным органом с прямым приоритетом. Установить зависимость среднего времени восстановления системы от закона распределения времени восстановления ее элементов.

Решение. Пусть распределение времени безотказной работы каждого элемента экспоненциальное с параметром λ, а время восстановления имеет гамма-распределение с плотностью средним Т_в = αβ и вероятностыо невосстановления

Тогда среднее время восстановления системы может быть найдено по формуле (см. гл. 7)

и, значит,

Исследуя это отношение в зависимости от α, получим графики, представлен­ные на рис. 3.3.

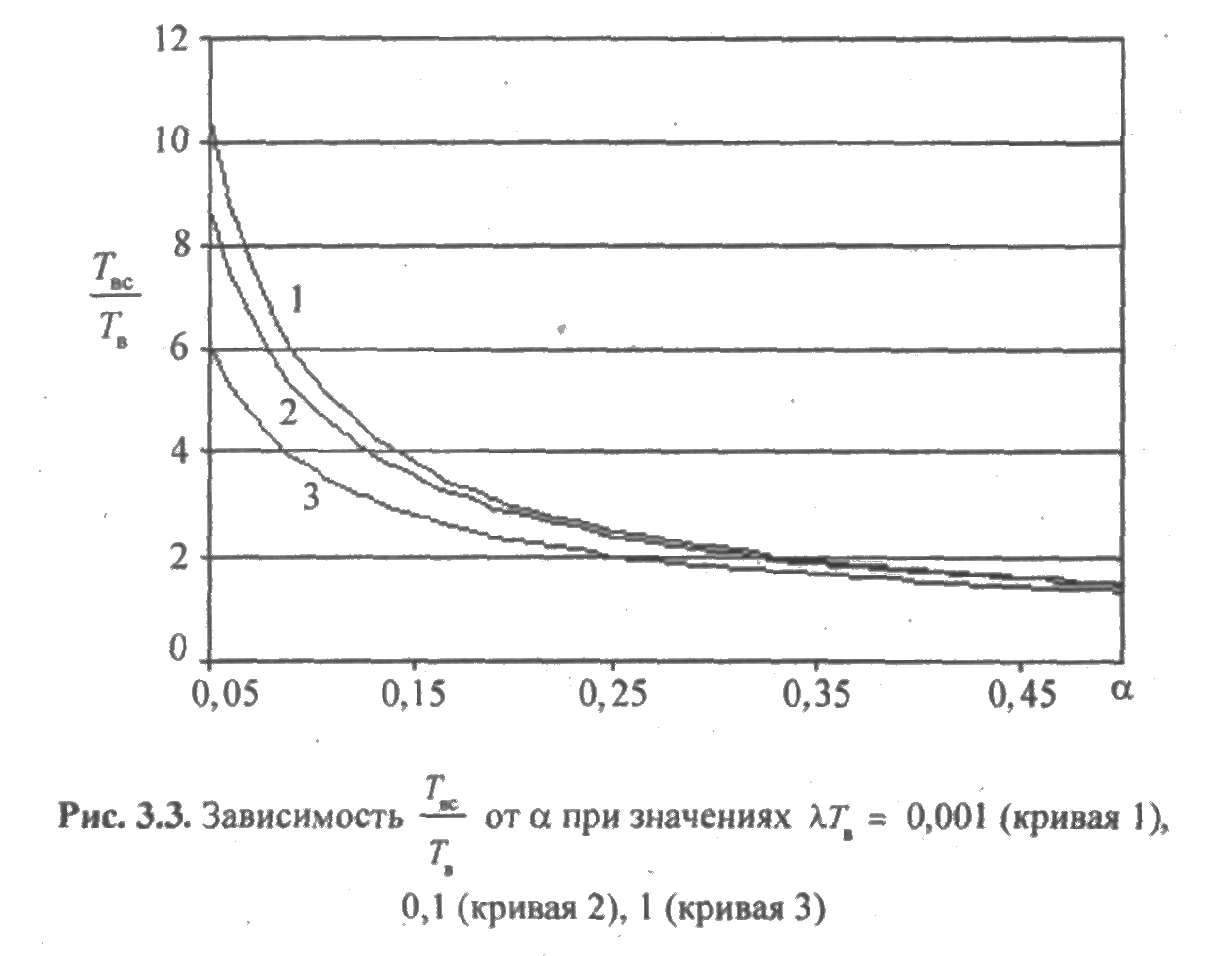
Таким образом, в зависимости от параметра α, а в общем случае — от закона распределения, можно получить характеристики надежности системы, изменяющиеся в достаточно широком диапазоне. При α = 1 имеем экспоненциальный случай, при котором Т_вс=Т_в.

Для неэкспоненциальных распределений некоторые показатели надежности не полно характеризуют систему и нечувствительны к ее изменениям.

ПРИМЕР 3.3. Дано: невосстанавливаемая резервированная система при общем резервировании с кратностью т-1. Определить выигрыш в надежности G_T=T_c/T₀ для распределений: экспоненциальное, Вейбулла, вырожденное, равномерное.

Решение. Пусть — вероятность безотказной работы, а T₀ — наработка до отказа одного элемента. Тогда для системы вероятность безотказной работы и средняя наработка до отказа вычисляются соответственно по формулам

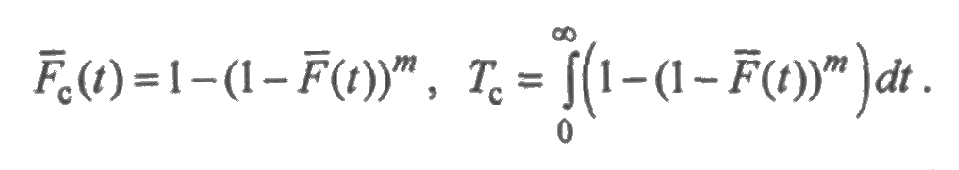
Для вырожденного распределения очевидно, что T_с = T₀ для любых значений т. Для распределения Вейбулла имеем

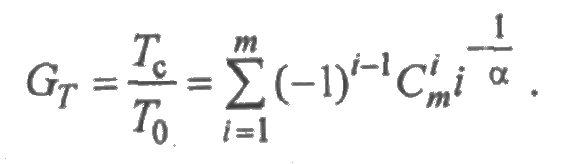
В частности, при α = 1 получаем экспоненциальное распределение, для которого

Для равномерного распределения с параметрами а и b

В частности, при а = 0 получим G_T=2m/m+1. Результаты расчетов по приведенным формулам сведем в табл. 3.1.

Как следует из таблицы, для вырожденного распределения наработка до отказа Т_с совершенно не чувствительна к числу резервных элементов. Для равномерного распределения резервирование также дает незначительный выигрыш (не более чем вдвое). Распределение Вейбулла при достаточно большом значении параметра α не оказывает существенного влияния с ростом т на изменение наработки до отказа. В то же время для распределения Вейбулла при молодеющем распределении можно получить любой сколь угодно большой выигрыш. Заметим, что для ненагруженного резерва G_T есть величина постоянная, равная т.

Приведенные примеры доказывают необходимость количественной оценки надежности систем при распределениях, отличных от экспоненциальных: она продиктована существенной зависимостью показателей надежности от законов распределения и дисциплины восстановления отказавших элементов.