2.6.2. Стационарные значения показателей надежности элемента

Получим предельные значения для показателей надежности восстанавливаемого элемента, предполагая, что с течением времени процесс функционирования элемента устанавливается и приобретает стационарный характер. Будем считать в дальнейшем, что f_k = f, g_k = g, k = 1, 2,... с математическими ожиданиями T и T_в соответственно.

Наиболее удобным способом вычисления предельных соотношений является представление характеристик в виде преобразования Лапласа.

Из равенств (2.29) следует, что параметры потоков отказов и восстановлений в изображениях имеют вид:

Следовательно, по свойствам (4) и (5) преобразования Лапласа (см. разд. 2.5) получим:

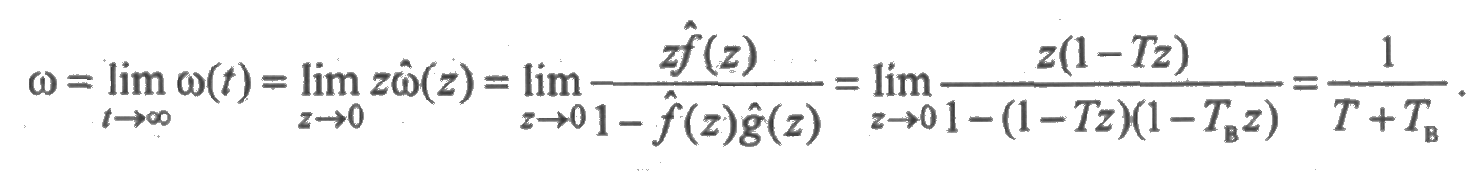
Аналогично

Таким образом, стационарные значения параметров потоков отказов и восстановлений одинаковы и равны

Из (2.32) следует, что

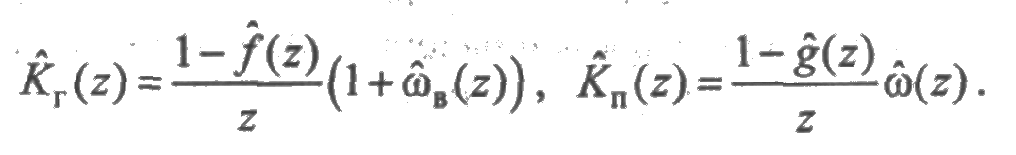
Следовательно, коэффициенты готовности и простоя равны соответственно

Коэффициент готовности определяется только средним временем работы элемента до отказа и средним временем восстановления вне зависимости от законов распределения. Это означает, что К_г нельзя применять для оценки надежности технических систем кратковременного использования. Более полная информация о работе такой системы содержится в функции готовности (см. рис. 2.11).

Получим предельные соотношения для среднего числа отказов и восстановлений. Вычислим предел разности при t→∞:

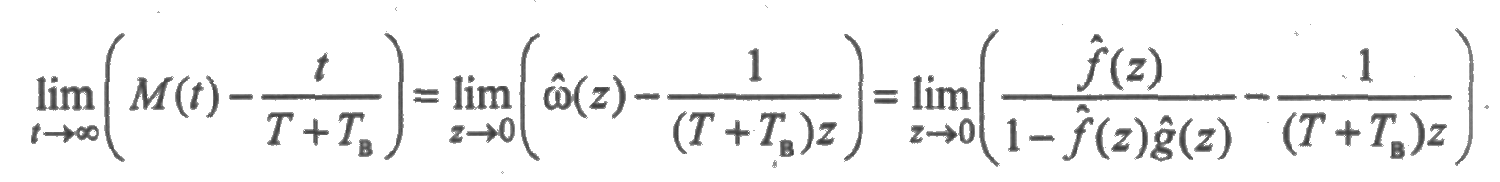
Применяя свойство (5) преобразования Лапласа, подучим

где α₂ и β₂ — вторые начальные моменты случайных величин с плотностями f(t) и g(t) соответственно. Отсюда следует асимптотическая оцени среднего суммарного числа отказов:

Аналогично при t→∞ имеет место асимптотическая оценка среднего суммарного числа восстановлений:

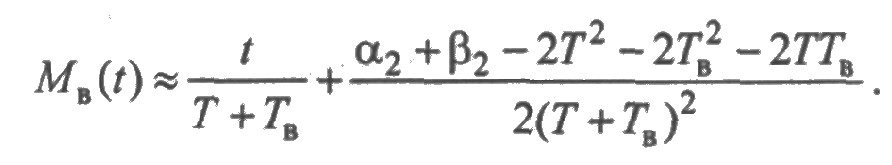
Похожие рассуждения позволяют найти асимптотические оценки для средней суммарной наработки и среднего суммарного времени восстановления элемента:

Теперь легко найти предельные соотношения для интенсивностей потоков отказов и восстановлений:

Вычислим стационарные значения средней наработки между отказами и среднего времени восстановления:

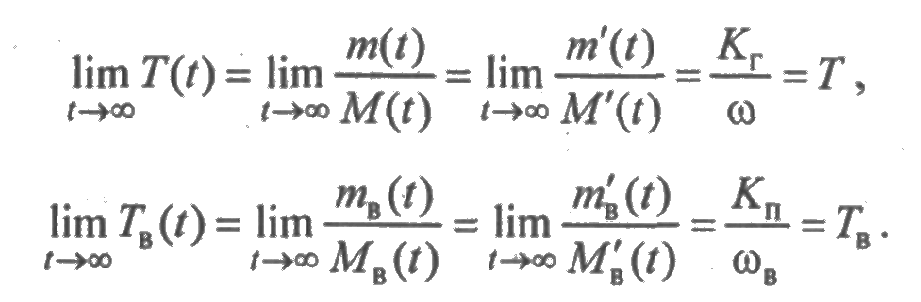
Как и следует ожидать, для стационарного режима средняя наработка между отказами равна среднему времени безотказной работы элемента.

2.6.3. Показатели надежности невосстанавливаемой и восстанавливаемой техники

В разд. 2.6.1 были введены показатели надежности элементов. Определим теперь показатели надежности системы. Пусть Е — множество состояний системы, k, l ϵ E— любые два состояния множества Е. Введем в рассмот­рение следующие случайные процессы и свяжем с ними определенные функции.

• ζ_k,l(t) — число переходов системы из состояния k в состояние l в течение времени [0;t], М_k,l(t)— математическое ожидание ζ_k,l(t), ω_k,l(t) = М’_k,l(t) — параметр перехода системы в момент времени t из состояния k в состояние l;

• χ_k(t) — суммарное время пребывания системы в состоянии k в течение времени [0;t], m_k(t) — математическое ожидание χ_k(t), p_k(t) = m’_k(t) — вероятность пребывания системы в момент времени t в состоянии k .

Определим теперь случайные процессы и некоторые производные от их функции для подмножеств состояний множества Е, где е и f — любые непересекающиеся подмножества множества состояний Е:

ζ_e,f(t) — число переходов системы из состояний множества е в состояния множества f в течение времени [0,t], M_e,f(t) — математическое ожидание ζ_e,f(t), ω_e,f(t) = М'_e,f(t) — параметр перехода в момент времени t из множества состояний е в множество состояний f;

χ_e(t)— суммарное время пребывания системы в состояниях множества e в течение времени [0;t], т_е(t)— математическое ожидание χ_e(t), p_e(t) = m’_e(t)— вероятность пребывания в момент времени t в каком-либо состоянии множества е.

Случайные процессы ζ_e,f(t) и χ_e(t) являются базовыми, поскольку через них может быть получена вся информация о работе системы с позиции теории надежности. Так, например, математические ожидания этих процессов позволяют определить среднее время Т_e,f(t)_е>/(1) пребывания системы в множестве е до перехода в множество f в течение времени [0;t]:

Интенсивность перехода системы в момент времени t из множества е в множество f определяется отношением:

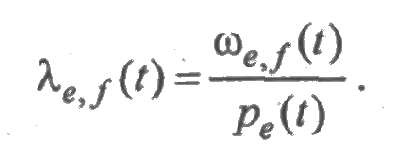
Укажем формулы связи между показателями, характеризующими множества состояний из Е и отдельные состояния множества Е: