2.5. Преобразование Лапласа

Многие числовые показатели надежности элементов и систем выражаются через функции типа свертки или бесконечными рядами, члены которых являются свертками функций. Для исследования таких показателей большую помощь может оказать преобразование Лапласа. Оно удобно также при расчетах предельных значений функций, лежит в основе операционного метода решения дифференциальных уравнений и систем. Преобразование Лапласа позволяет преобразовать любую систему обыкновенных дифференциальных уравнений в систему линейных алгебраических уравнений.

Пусть функция f(t) кусочно-непрерывна при t≥0 и имеет ограниченный рост, т. е.

где С и α — некоторые постоянные. Тогда она называется оригиналом, а функция

— ее изображением. Переход от оригинала к изображению называется преобразованием Лапласа, а переход от изображения к соответствующему оригиналу — обратным преобразованием Лапласа. В дальнейшем вместо 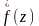будем иногда писать f(s).

Перечислим некоторые полезные свойства преобразования Лапласа.

1. Изображение линейной комбинации функций равно линейной комбинации изображений: если

2. Изображением производной f'(t) является функция

3. Изображение свертки функций равно произведению изображений сомножителей: если

4. При вычислении предельных значений функций можно использовать равенство

Заметим, что данное свойство не всегда верно. Так, например, если f(t) представляет собой сумму δ-функций, т. е.

то предел вообще не существует. Однако:

5. Если f(t) — плотность распределения вероятностей неотрицательной случайной величины X, то ее изображение удовлетворяет соотношениям:

В частности,

где Т — математичес ожидание, а α₂ — второй начальный момент случайной величины X.

Решение системы алгебраических уравнений, полученной по системе линейных дифференциальных уравнений, образуют дробно-рациональные функцию вида

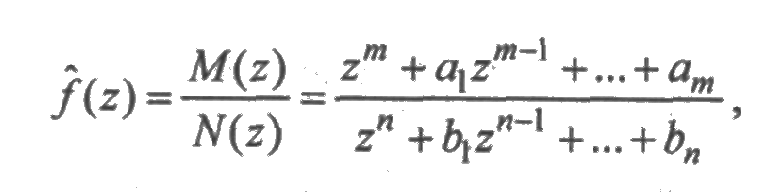
причем т<п. Если знаменатель дроби N(z) имеет только простые корни z₁, z₂,..., z_n, то оригинал определяется равенством

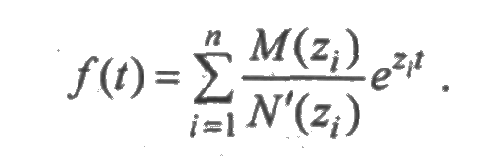
Если знаменатель дроби N(z) имеет кратные корни: z₁ кратности r₁, z₂ кратности z₂,..., z_k кратности r_k (r₁ + r₂ +...+r_k = n), то оригинал определяется равенством

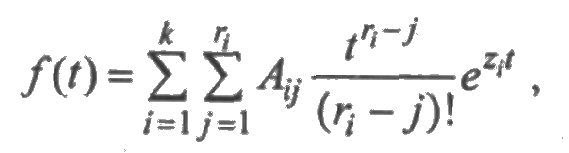
где коэффициенты А_ij находятся по формулам:

2.6. Специальные показатели надежности элементов и систем

2.6.1. Показатели надежности элемента

Работу восстанавливаемого элемента с двумя состояниями можно представить в виде последовательности интервалов исправной работы ξ_k и интервалов восстановления η_k, чередующихся друг за другом, как показано к рис. 2.8.

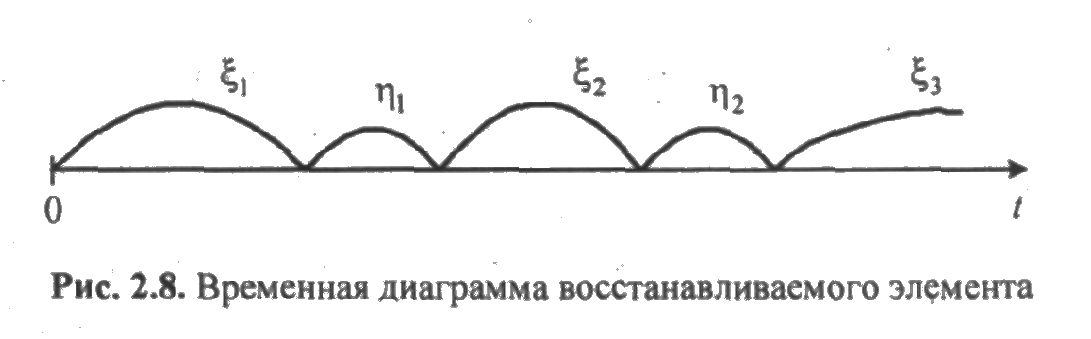
Предположим, что случайные величины ξ_k и η_k независимы и имеют плотности f_k(t) и g_k(t) соответственно. Обозначим через F_k(t) и G_k(t) функции распределения сумм соответственно, а через F_k,l(t) — функцию распределения суммы случайных величин 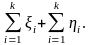Предположим также, что F₀(t) и G₀(t) =1.

Рассмотрим следующие случайные процессы ζ(t) и ζ_B(t), равные соответственно числу отказов и числу восстановлений элемента за время [0;t]. Это дискретные случайные процессы с непрерывным временем. Обозначим через М(t) = М(ζ(t)) и М_B(t)=M(ζ_B(t)) их математические ожидания (в предположении, что они существуют). Функции М(t) и М_B(t) характеризуют среднее число отказов и среднее число восстановлений элемента за время [0; t ]. Если в момент времени t=0 элемент был исправен, то очевидно, что М(t)≥М_B(t) для любого t.

Определим скорости изменения среднего числа отказов ω(t) = М'(t) и среднего числа восстановлений ω_в(t) = М'_B(t). Функции ω(t) и ω_в(t) называются параметрами потоков отказов и восстановлений соответственно. Принимая во внимание, что М(0) = М_B()) = 0, получим

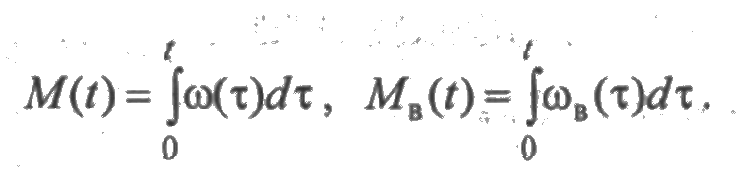
Рассмотрим случайный процесс χ(t), как суммарное время работы (наработка) элемента, и случайный процесс χ_в(t), как суммарное время восстановления элемента за время [0; t]. Это есть непрерывные случайные процессы с непрерывным временем (на самом деле функции распределения в одной точке терпят разрыв). Обозначим через m(t) = М(χ(t)) и m_в(t) = М(χ_в(t)) - математические ожидания этих случайных процессов. Функции т(t) и т_в(t) показывают среднюю наработку и среднее суммарное время восстановлена элемента в течение времени [0;t]. Функция готовности К_г(t) и функция простоя К_П(t) элемента определяются как вероятности того, что в момент t элемент находится в состоянии работоспособности и в состоянии восстановления. Далее в этом разделе будет показано, что К_г(t) = т'(t), К_П(t)= т_в(t).

Разделив среднюю наработку на среднее число отказов элемента за время [0;t], получим среднее время работы элемента между отказами, или наработку на отказ. Тогда среднее время работы элемента между отказами в течение времени [0;t] определится отношением:

Аналогично определяется среднее время восстановления элемента в течение времени [0;t], как отношение среднего суммарного времени восстановления элемента на среднее число восстановлений:

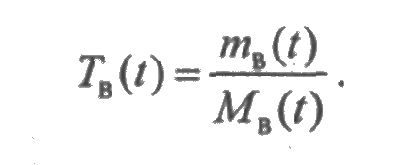
Интенсивности потоков отказов и восстановлений в момент t определим равенствами

Получим представление введенных характеристик через плотности и функции распределения случайных величин ξ_k и η_k.

Любое сечение случайного процесса ζ(t) есть случайная величина дискретного типа с возможными значениями k=0,1,2,... и вероятностями р_k(t), Поскольку р_k(t) - вероятность того, что за время [0;t] произошло ровно k отказов, то

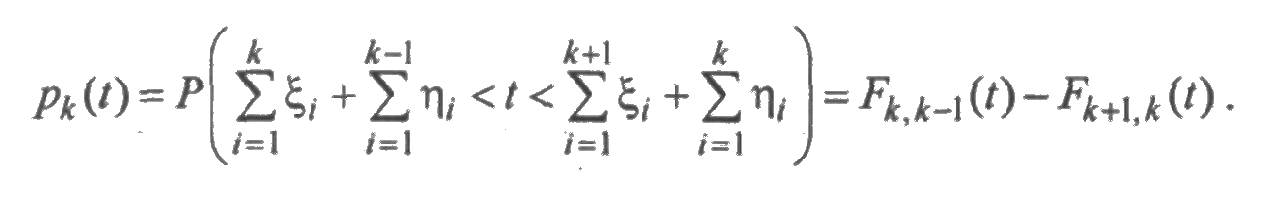
Поэтому математическое ожидание случайной величины ζ(t) равно

откуда

Аналогично для случайного процесса ζ_В(t) математическое ожидание равно

Параметры потоков ω(t) и ω_B(t) были определены как производные от математических ожиданий числа отказов и числа восстановлений элемента за промежуток времени [0; t]. Дадим теперь иное, локальное в некотором смысле, но эквивалентное первоначальному, определение этих параметров. Пусть р(t,t+Δt) — вероятность отказа элемента за время [t, t+Δt], а р_B(t,t+Δt) — вероятность того, что за промежуток времени [t,t+Δt] элемент будет восстановлен. Тогда

т. е. параметры потоков отказов и восстановлений равны соответственно вероятностям отказа и восстановления за малый промежуток времени, отнесенным к длине этого промежутка. Эквивалентность определений видна из следующих соотношений:

Используя (2.12), получим:

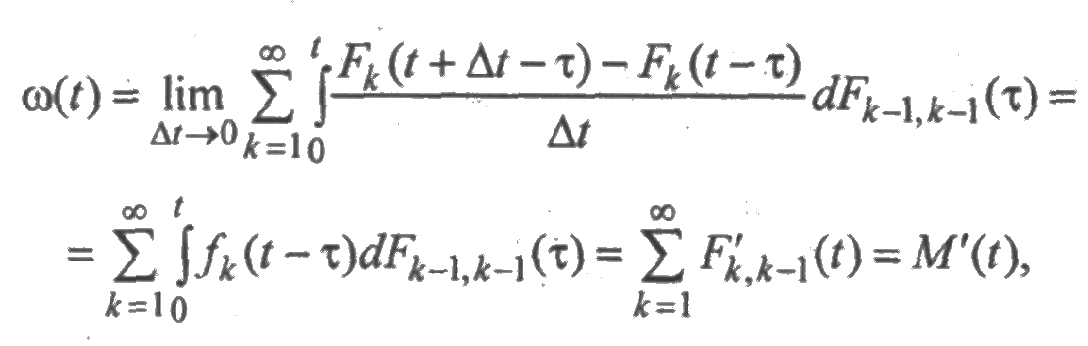
что и доказывает равносильность двух определений функции ω(t). Подобные рассуждения справедливы и для функции ω_B(t).

Из определения интенсивностей потоков отказов и восстановлений, а также из равенств (2.24) получаются следующие выражения для λ(t) и ω(t):

Из этих формул следует, что интенсивность потока отказов есть вероятность отказа за малый промежуток времени [t, t+Δt] при условии, что в момент t элемент находится в исправном состоянии, отнесенная к длине этого промежутка. Интенсивность потока восстановлений есть вероятность восстановления в течение времени [t, t+Δt] при условии, что в момент t элемент находится в состоянии восстановления, отнесенная к длине этого промежутка.

Перейдем к изучению случайных процессов χ(t) и χ_в(t). Рассмотрим случайный процесс χ(t), равный суммарному времени работы элемента в течение времени [0; t]. Зафиксируем момент времени t ₀ и найдем закон распределения случайной величины χ(t₀).

Пусть F(t) — функция распределения случайной величины χ(t₀). Очевидно, что F(t) = 0 при t< 0 и F(t) =1 при t > t₀. Из временной диаграммы, изображенной на рис. 2.8, следует, что при 0<t< t₀

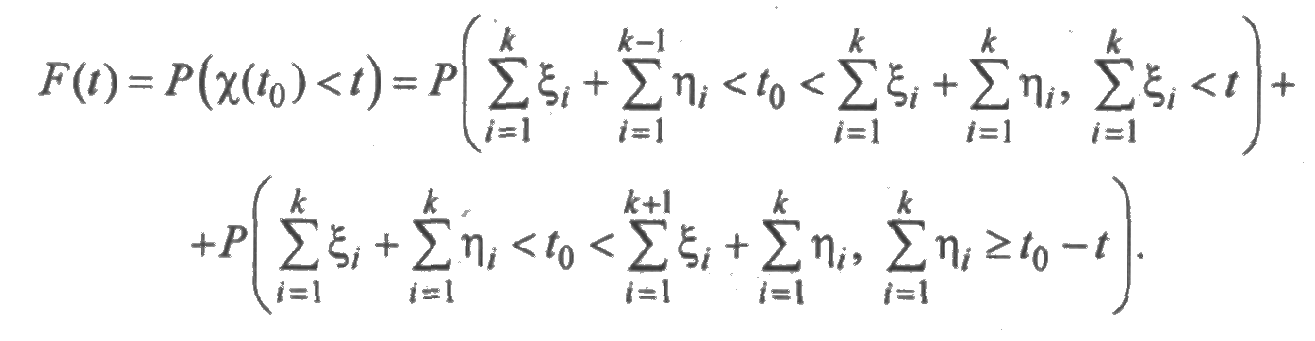
Из принятых ранее обозначений следует, что

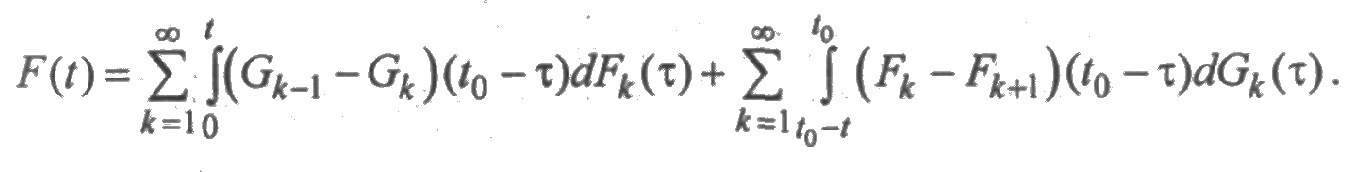
Преобразуя эти выражения, получим

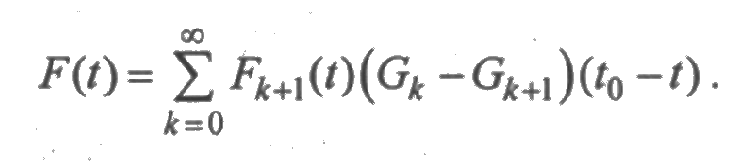
График функции F(t) представлен на рис. 2.9.

Функция F(t) имеет в точке t₀ разрыв, поскольку F(t₀ - 0) = F₁(t₀), и величина скачка равна 1 - F₁(t₀). Вычислим математическое ожидание случайной величины χ(t₀). Для случайной величины смешанного типа

Таким образом, средняя суммарная наработка системы за время [0;t] равна

Рассмотрим случайный процесс χ_в(t) равный суммарному времени восстановления элемента в течение времени [0;t]. Можно показать, что при 0<t<t₀ закон распределения случайной величины χ_в(0) характеризуется функцией распределения

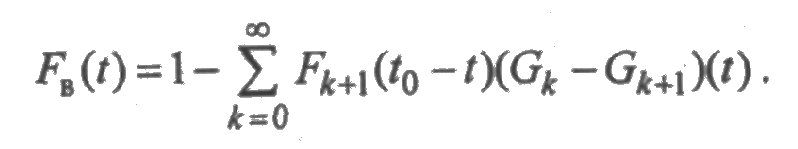
Полученная зависимость иллюстрируется графиком на рис. 2.10.

Математическое ожидание случайной величины χ_в(0) равно

и, значит, среднее суммарное время восстановления элемента за время [0;t] составляет

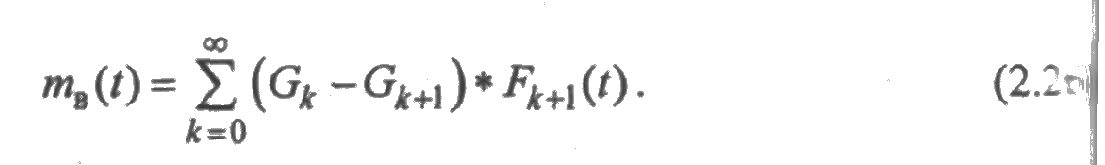
Складывая ряды (2.25) и (2.26), убеждаемся в том, что т(t)+ m_в(t)=t. Вычислим функции готовности и простоя. Очевидно, что

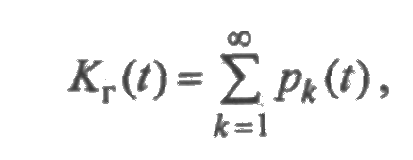
где р_к(0) - вероятность того, что момент времени t приходится на k-й интервал исправной работы элемента. Поскольку

то

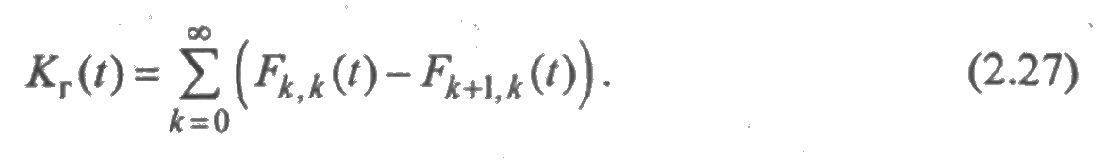
Таким же образом доказывается формула

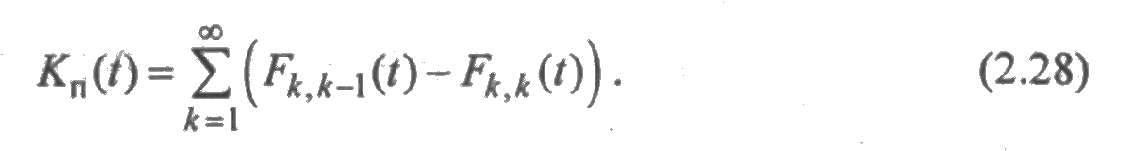
Дифференцируя функции т(t) и то, т_B(t) и сравнивая производные с выражениями (2.27) и (2.28), видим, что

В частности, если законы распределения времени исправной работы на каждом интервале одинаковы и имеют плотность f(t), а законы распределения времени восстановления имеют плотность g(t), то соотношения для введенных характеристик можно записать в более компактном виде. Будем обозначать через f*^(k) k-кратную свертку функции f. Тогда из (2.23) получим сле­дующие выражения для параметров потоков:

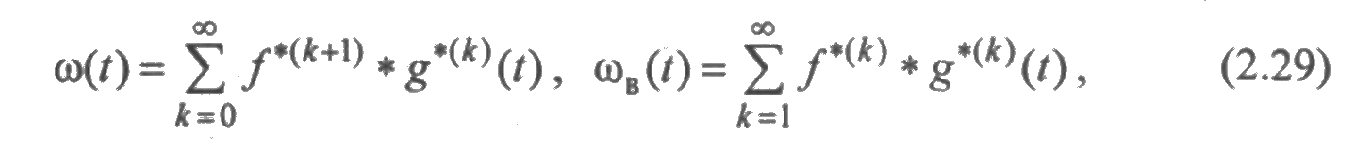
откуда следуют зависимости

Для функций готовности и простоя из (2.27) и (2.28) будем иметь

где

вероятность безотказной работы элемента в течение времени t, а

вероятность того, что за время t элемент не будет восстановлен.

Из (2.31) следует, что

ПРИМЕР 2.6. Время до отказа элемента имеет нормальное распределение с параметрами α = 1000 час, s = 300 час. Время восстановления имеет нор­мальное распределение с параметрами b=10 час, r = 30 час. Требуется определить функцию готовности.

Решение. Вычислим функцию готовности по формуле (2.27). По свойству нормального распределения функции F_k,k(t) и F_k,k+1(t) также являются функциями нормального распределения с параметрами т_k = k(а + b), 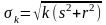и m_k + α, соответственно. Поэтому, используя функцию Лапласа, получим

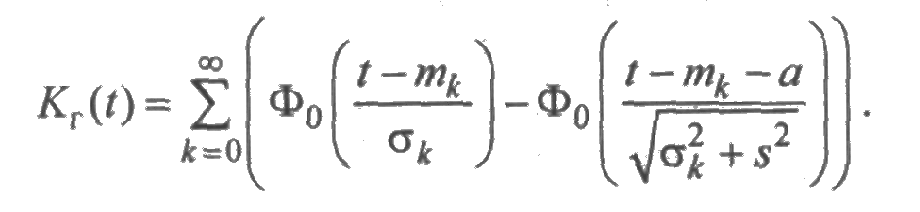
Расчеты, выполненные по этой формуле, позволяют построить график функ­ции готовности (рис. 2.11).

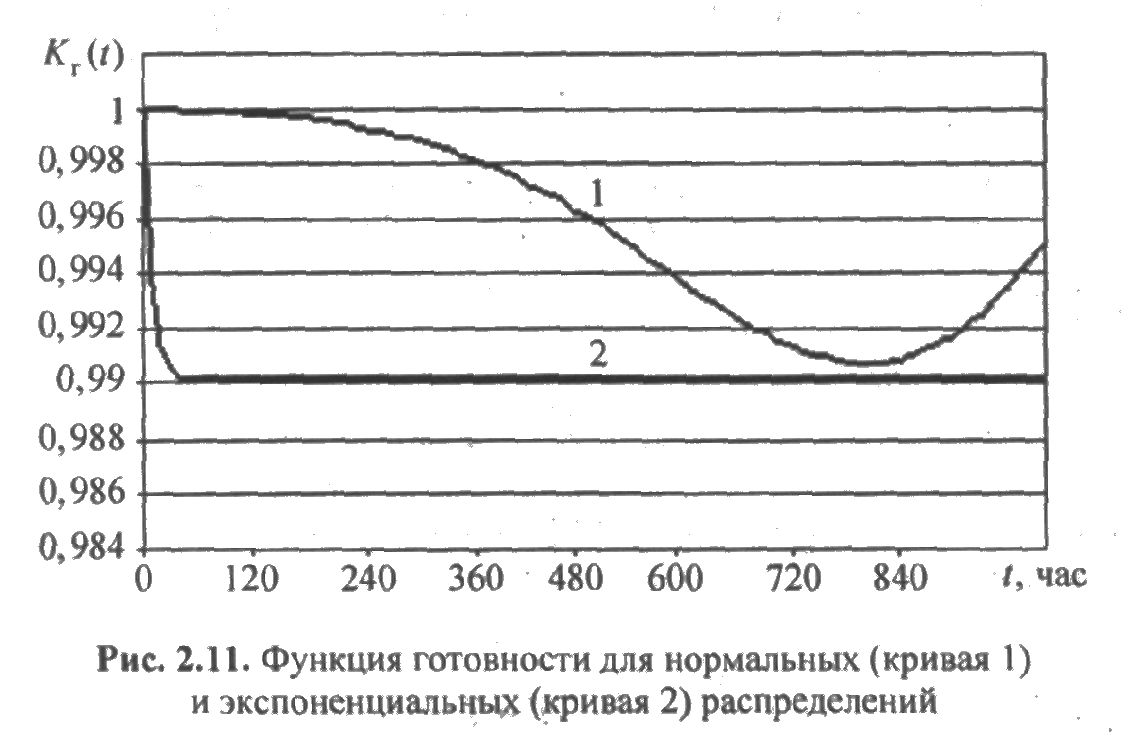
Для сравнения на этом же рисунке изображен график функции готовности, если время до отказа и время восстановления элемента имеют экспоненциальные распределения со средними а и b соответственно.

Различие двух кривых очевидно. Функция готовности для случая нормального распределения имеет колебательный характер, отсутствующий у системы с экспоненциальным законом распределения отказов и восстановлений. Стационарный режим в первом случае долго не наступает, во втором он наступает практически мгновенно.