15. Прямые методы решения слау. Метод прогонки.

Метод решения задачи называют прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Если эта последовательность сходится к решению задачи, то говорят, что итерационный процесс сходится. К прямым методам решения относятся метод Гаусса и его модификации, метод Холецкого и метод прогонки.

В методе Гаусса для вычисления масштабирующих множителей требуется делить на ведущие элементы каждого шага. Если элемент равен нулю или близок к нулю, то возможен неконтролируемый рост погрешности.

Поэтому часто применяют модификации метода Гаусса, обладающие лучшими вычислительными свойствами.

Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент a_ikiпри неизвестной x_k в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером i_k, меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента a_kk^k-1. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

15. Итерационные методы решения слау.

По своей сути, итерационный метод заключается в выполнении некоторого итерационного процесса до тех пор, пока решение системы уравнений не будет найдено с необходимой точностью. В свою очередь итерационный процесс на каждом своем шаге строит некоторое приближение искомого решения.

Метод Якоби (метод простой итерации)

Данный метод решения систем линейных алгебраических уравнений был предложен немецким математиком Карлом Якоби (1804 - 1851). Итерационный процесс в этом методе имеет вид: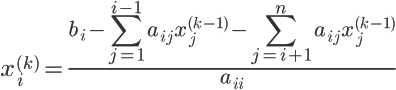 где - номер неизвестной, а - номер итерации алгоритма.

Метод Зейделя

Этот метод решения систем линейных алгебраических уравнений был предложен немецким математиком и астрономом Филлипом Людвигом Зейделем (1821 - 1896). Итерационный процесс в этом методе имеет вид:

Этот метод решения систем линейных алгебраических уравнений был предложен немецким математиком и астрономом Филлипом Людвигом Зейделем (1821 - 1896). Итерационный процесс в этом методе имеет вид:

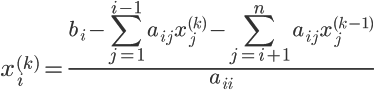
где - номер неизвестной, а - номер итерации алгоритма.

15. Аппроксимация функций. Постановка задач и способы ее решения.

Аппроксимация (от латинского "approximate" -"приближаться")- приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов.

15. Интерполяционные методы Лагранжа.