2. Общие принципы работы оптических спектральных приборов

2.1. Спектральный прибор как линейная система

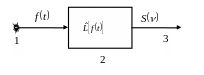
Рассматривая вопросы, связанные с существующими модификациями приборов, предназначенных для анализа оптических спектров, прежде всего остановимся на самых общих принципах их построения и функционирования. Рассмотрим условную схему работы спектрометра (рис. 2.1). Электромагнитная волна , испущенная источником 1, попадает на вход устройства 2, действие которого на волну описывается оператором . В результате его работы на выходе мы получаем функцию , характеризующую спектр процесса (подразумевая при этом фурье-спектр).

Рис. 2.1

Устройство 2 состоит из оптической системы, приемника излучения и системы обработки сигналов, представляющей их в форме, удобной для дальнейшего анализа. Каждый из этих элементов с необходимостью присутствует в любом спектрометре, даже в простейшем спектроскопе, где функции последних двух частей выполняют глаз и мозг человека.

Чисто формально, задачей спектрометра является возможность

- различить участки спектра с разными частотами,

- измерить амплитуды каждого участка.

Задача различения – «разрешения» – отдельных спектральных составляющих может быть осуществлена разными способами. В приборах, основанных на «классических» принципах, она решается путем направления излучения с разными частотами под разными углами по отношению к устройству-анализатору. Приборы, отнесенные мною в предыдущем издании к «новым», используют различные методы модуляции во времени разных компонентов спектра. Например, в монохроматорах с растрами и в сисаме вначале происходит грубое разделение спектра исследуемого источника одним из известных с XIX века элементов, разворачивающим излучение по углам, и модулируется уже только узкий спектральный интервал. В фурье-спектрометрах каждому компоненту спектра сообщается своя частота модуляции, разделение компонентов на основании измерения этой частоты осуществляется на следующем этапе анализа. Принципы цифрового кодирования частотных компонентов входного светового потока после пространственного их разделения используются в адамар-спектроскопии.

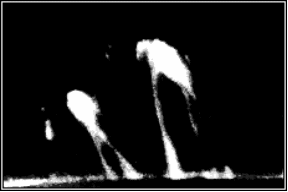
Значительная (подавляющая) часть спектральных приборов не предназначена для изучения пространственных свойств источников, хотя фотографии протуберанцев, полученные с помощью одноканального спектрографа в излучении линии были, в свое время, показаны в учебниках астрономии для 10-го класса средней школы (рис. 2.2),

Рис. 2.2 Фотография протуберанца в свете линии водорода Hα.

а с такими устройствами как диафрагма Гартмана и трехлинзовый конденсор, которые позволяют выделить излучение только небольшого участка источника, знаком любой спектроскопист. Вместе с тем, решение многих современных проблем, требующих резкого увеличения количества информации именно об особенностях спектрального распределения излучения в пространстве, привело к развитию соответствующих модификаций спектральных приборов. Этому, конечно, способствовало фантастическое увеличение скорости обработки информации компьютерами, происшедшее с момента издания предыдущего варианта книги.

Одним из наиболее общих требований, предъявляемым к спектральными приборам, является линейность. Что касается линейности оптической части классического прибора, то она выполняется практически всегда и нарушается иногда только для лазерного излучения большой мощности. Приемно-регистрирующее устройство спектрометра бывает как линейным, так и нелинейным. Примером последнего может служить фотопластинка, или фотоумножитель с логарифмическим усилителем сигнала. Обычно же стремятся к тому, чтобы и приемник излучения, и система обработки сигнала работали в линейном режиме.

В книге мы всегда будем предполагать, что все элементы спектрального прибора удовлетворяют условию линейности по амплитуде световой волны. Это означает, что при одновременном действии на входе прибора нескольких сигналов отклик прибора будет описываться суммой , где . Соответственно, в схеме рис. 2.1 оператор всегда будет считаться линейным.

Предположим, что сигнал таков, что к нему можно применить преобразование Фурье, т. е. его можно представить в виде линейной комбинации гармонических колебаний:

(2.1 а)

(2.1 б)

Теперь достаточно было бы зарегистрировать амплитуды и фазы колебаний , чтобы получить спектр исходного процесса. При такой постановке вопроса мы игнорируем, однако, две принципиальные особенности работы прибора в оптическом диапазоне частот электромагнитного излучения. Во-первых, все реальные приемники реагируют не на амплитуду волны, а на поток энергии или спектральную плотность потока, которые пропорциональны произведению . Во-вторых, подавляющее большинство спектроскопических задач связано с анализом излучения источников, у которых амплитуда и фаза волны испытывают случайные флюктуации (исключение составляют лишь лазеры). Непосредственное применение соотношений (2.1) к случайной функции дает также случайную функцию. Для того чтобы охарактеризовать случайный процесс детерминированным образом, рассматривается спектр его мощности:

(2.2)

Обратным преобразованием является функция автокорреляции сигнала :

.

(2.3)

Будучи нормирована, она называется в оптике функцией временной когерентности.

Связь между и дается парой преобразований Фурье:

(2.4)

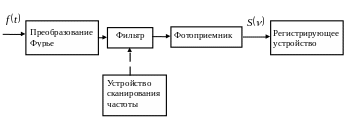
Из соотношений (2.2), (2.3) и (2.4) видно, что возможны две схемы построения спектрометра. В первой электромагнитная волна проходит через фильтр, выделяющий узкую полосу частот , и затем попадает на приемник, регистрирующий мощность данной спектральной составляющей. Полный спектр получают путем последовательной перестройки одного фильтра на разные частоты («сканирование» спектра), или установкой большого числа параллельно действующих фильтров. Во второй схеме регистрируется функция автокорреляции входного процесса, а спектр мощности находят путем вычисления ее фурье-образа. Представим эти две возможности в виде следующих схем (рис. 2.3).

Первой из них (рис. 2.3 а) соответствуют все классические приборы — монохроматоры и спектрографы с призмами и дифракционными решетками, приборы высокой разрешающей силы с интерферометрами, а также сисам. Сюда же, вероятно, следует отнести квантометры и, с некоторой натяжкой, спектрометры с преобразованием Адамара. Второй принцип измерения (рис. 2 б) реализуется в фурье-спектрометрах. Успехи развития вычислительной техники привели к тому, что специализированные ЭВМ, встроенные в прибор, позволяют наблюдать в процессе измерений сам спектр, и внешнее различие между фурье-спектрометром и классическим спектрометром исчезает.

Рис. 2.3 а

Рис. 2.3 б

Применение перестраиваемых лазеров с очень узкой линей генерации изменяет схему спектроскопического эксперимента. В качестве примера приведу еще две схемы. Начну с того, что к представленным на рис. 2.3 а,б системам добавлю еще одну. Она использовалась и ранее в эпоху «классической» оптики при измерениях в абсорбционной спектроскопии, но обрела совершенно новую жизнь и свойства в лазерную эпоху. Для ее реализации нужен только источник монохроматического излучения, априорно «настроенный» на линию поглощения исследуемого вещества, и фотоприемник (рис. 2.4 а). Если раньше в качестве такого источника применялась, как правило, лампа Белла-Блюма, излучающая необходимые узкие линии (обычно использовался и спектральный прибор, но требовался он только для того, чтобы уменьшить фоновую засветку), то при наличии перестраиваемого лазера проблема фона практически снимается, настолько мощность его излучения превосходит мощность внешнего (теплового, или рассеянного).

Создание перестраиваемых одночастотных лазеров позволяет решить и задачу измерения амплитуды волны. Здесь мы попадаем в область нелинейной «спектроскопии смешения», когда используется линейность фотоприемника по мощности падающей на него светового потока, то есть квадратичную нелинейность по амплитуде волны. Метод по своей идее полностью аналогичен гетеродинному приему в радиотехнике (рис. 2.4 б)

Рис. 2.4 а

Рис. 2.4 б

Последний рисунок требует пояснений. Напомню, что задача измерения – это задача сравнения измеряемой физической величины с эталоном. Предположим, что необходимо измерить неизвестную амплитуду колебаний поля лазера, излучающего монохроматическую волну на частоте , а в нашем распоряжении имеется эталонный перестраиваемый лазер, работающий на частоте и создающий на фотоприемнике поле с амплитудой . Будем оперировать вещественными величинами и отвлечемся пока от проблемы измерения фазы, тем более что разность фаз колебаний при линейно меняется со временем. На фотоприемник действуют одновременно два колебания:

(2.5)

По условию задачи отклик фотоприемника считаем пропорциональным мощности (т. е. квадрату суммы этих амплитуд)¹:

Как мы видим, в отклике фотоприемника наблюдается постоянная составляющая, пропорциональная сумме квадратов амплитуд, компоненты с удвоенной и суммарной частотой, а также самое интересное – последнее – слагаемое в квадратных скобках. Если учесть, что говоря об оптических процессах, мы имеем дело с частотами выше 10¹² Гц, а инерционность фотоприемников обычно превосходит 10^-11 – 10^-10 с, то усреднение по такому промежутку времени высокочастотных составляющих даст нуль. Только слагаемое с разностной частотой останется ненулевым. Обозначив усреднение по времени угловыми скобками, этот результат запишем в виде:

(2.6)

Измеряя амплитуду колебаний отклика фотоприемника (например, тока фотоэлемента) на этой разностной частоте, мы измеряем амплитуду (сравниваем с амплитудой ) световых колебаний на частоте . В более простом варианте этот метод был применен уже для анализа спектра излучения первого многомодового гелий-неонового лазера в 1962 году. Регистрировались комбинации между различными продольными модами. Разностные частоты при этом лежали в диапазоне сотен мегагерц, для исследования которых использовались радиочастотные спектрометры. Отмечу, что потребность в спектрометре (или, по крайней мере, фильтре, настроенном на разностную частоту) при этом не отпадает – просто происходит перенос спектра в новый, более удобный для анализа, диапазон частот. Таким образом, схема спектральных измерений в общем случае соответствует рис. 2.4 б, а в конкретном варианте гелий-неонового лазера она выглядит так, как это показано на рис. 2.5:

Рис. 2.5