8.4. Основы организации контрольных испытаний

Для проведения контрольных испытаний из совокупности (партии) однородных приборов составляется некоторая выборка и проводятся испытания на надежность попавших в эту выборку приборов. По результатам испытаний выборки делается вывод о соответствии всей партии предъявляемым требованиям.

Математический аппарат решения этой задачи - изучаемые в математической статистике методы проверки статистических гипотез. В качестве нулевой (проверяемой) гипотезы принимается предположение о том, что партия соответствует предъявляемым требованиям. Противоположной (альтернативной) является гипотеза о том, что партия не удовлетворяет этим требованиям.

По результатам испытаний имеет место одна из четырех возможных ситуаций:

1. Партия удовлетворяет требованиям; по результатам испытаний выборки подтвердилась нулевая гипотеза Н₀ и принято решение о принятии всей партии. Это решение правильно.

2. Партия удовлетворяет требованиям надежности, но по результатам испытаний выборки нулевая гипотеза не подтвердилась. Это произошло потому, что случайная выборка содержала повышенную долю бракованных образцов по сравнению с долей образцов в партии. Принята альтернативная гипотеза – Н₁; это решение неправильно и невыгодно для изготовителя приборов. Вероятность принятия этой ошибочной гипотезы - α называется риском поставщика.

3. Партия не удовлетворяет требованиям, по результатам испытаний выборки нулевая гипотеза не подтвердилась. Принята альтернативная гипотеза - Н₁, то есть решение о непринятии партии. Это решение правильно.

4. Партия не удовлетворяет требованиям по надежности, но по результатам испытаний выборки подтвердилась нулевая гипотеза - Н₀. Принято неверное решение о принятии партии с большой долей бракованных изделий. Принято неверное решение, которое невыгодно потребителю. Вероятность этого неверного решения называется риском заказчика - β.

Естественно желание снизить значения обеих ошибок, доведя их в пределе до нуля. Зависимость вероятности L приемки партии от показателя надежности А ( называемая оперативной характеристикой плана контроля) для такой наилучшей ситуации приведена на рис. 8.3. Пусть А_тр - требуемое значение показателя надежности. В этой ситуации нулевая гипотеза - А А_тр. Если она справедлива, то партия принимается с вероятностью 1.

Рис. 8.3. Идеальная оперативная характеристика плана контроля

При этом α = 0. Альтернативная гипотеза заключается в том, что А < А_тр. В этой ситуации партия бракуется с вероятностью 1, причем β = 0. Однако такая идеальная оперативная характеристика требует бесконечного числа наблюдений.

В

реальной ситуации вводятся два уровня контролируемого показателя надежности : приемочный - А_α и браковочный - А_β ( см. рис. 8.4). Если А А_α,, то приборы должны приниматься с достаточно высокой вероятностью, не ниже L(А_α), если А < А_β, то приборы должны браковаться с достаточно высокой вероятностью, не ниже L(1- А_β). При этом риск поставщика α = 1- L(А_α), риск потребителя β = L(А_β). Таким образом, задача проверки статистических гипотез будет сформулирована так: проверяется нулевая гипотеза - А А_α против альтернативной А< А_β. Обычно риск поставщика α и потребителя β выбирается равным 0,1…0,2. Значение браковочного А_β и приемочного уровня А_α выбирается по договоренности между поставщиком и потребителем. Контрольные испытания на безотказность проводятся одноступенчатым или двухступенчатым методом.

Метод однократной выборки предполагает оценку надежности по выборке объемом n за время испытаний t_и по количеству полученных отказов m и заданных нормативах доли дефектных изделий q₀ и q_m (q₀ < q_m). Известно максимально допустимое число отказавших образцов в выборке с, при котором партия будет принята.

L

1

1-α

β

β

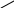
А

А_β А_тр А_α

Рис. 8.4. Реальная оперативная характеристика плана контроля

Таким образом, гипотеза H₀ принимается при значении отказавших образцов в выборке - m c (партия принимается), при m > c принимается альтернативная гипотеза Н₁ (партия бракуется). Исходными данными для проведения испытаний методом однократной выборки являются значения q₀, q_m, α, β. Число приборов, отказавших за время испытаний, подчиняется биномиальному распределению, поэтому вероятность наступления m отказов при нулевой и альтернативной гипотезе определяется так (см. п. 3.2.1):

, (8.14)

. (8.15)

Из системы уравнений (8.14, 8.15) можно найти неизвестные значения n – (объем выборки) и приемочное число отказавших образцов – с.

При применении двухступенчатого метода контроля определяют объемы выборок n₁, n₂ и приемочные числа – с₁ и с₂, зависящие от принятых q₀, q_m, α, β.

Образцы, вошедшие в первую выборку, испытываются в течение времени t₁ и определяют число наступивших отказов – m₁. Если m₁ с₁, то результаты контрольных испытаний положительны. Если m₁> с₁ + с₂, то испытания прекращаются, а результаты их считаются отрицательными. Если с₁< m₁ с₁ + с₂, то проводят испытания второй ступени.

Образцы изделий, вошедшие во вторую выборку, также испытывают в течение времени t₁. По окончании второй ступени определяют суммарное число отказов - m₁ и m₂. Если m₁ + m₂ с₁ + с₂, то результаты испытаний положительны, если m₁ + m₂ > с₁ + с₂, то результаты испытаний отрицательны.

Одноступенчатый метод при прочих равных условиях обеспечивает минимальную календарную продолжительность испытаний, двухступенчатый при тех же условиях позволяет обеспечить минимум среднего объема испытаний.

_________________________

1. Голинкевич Т.А. Прикладная теория надежности: учебник для вузов / Т.А. Голинкевич. М.: Высшая школа, 1977.

2. Ястребенецкий М.А. Надежность автоматизированных систем управления технологическими процессами / М.А. Ястребенецкий, Г.М. Иванова. М.: Энергоатомиздат, 1989.

3. Гнеденко Б.В. Математические основы теории надежности / Б.В. Гнеденко, Ю.К. Беляев, А.Д. Соловьев. М.: Наука, 1966.