6. Графіки варіаційних рядів, їх властивості

Для того, щоб наочно мати уявлення про характер розподілу, застосовують крім табличного ще графічне задання статистичних рядів розподілу. Основними способами графічного задання рядів розподілу є: огіва, гістограма, полігон і кумулята. Їх будують у прямокутній системі координат, де на горизонтальній осі абсцис відкладають значення варіантів, а на вертикальній осі ординат – частоти (частості), щільність відносних частот або нагромаджені частоти.

Огіва – графічне задання (зображення) ранжированого ряду розподілу. На осі абсцис відкладено номер варіанта досліджуваної ознаки ранжированого ряду, а на осі ординат – значення досліджуваної ознаки (варіанти).

У таблиці Ж.2.4 представлено ранжирований ряд господарств району, де одиниці сукупності розміщені в порядку зростання врожайності зернових культур. Ранжирування є початковим етапом побудови варіаційних рядів розподілу. Його використосувають для графічного зображення інтенсивності й швидкості зміни досліджуваної ознаки (рис.Ж.2.3).

Найчастіше варіаційні ряди зображують у вигляді полігона – многокутника розподілу. Полігон частот – замкена ламана, відрізки якої послідовно з’єднують точки з координатами координати , , ..., , ..., , де – значення випадкової величини, а – відповідні їм частоти (рис. Ж.2.4).

Аналогічно означається і будується полігон відносних частот для випадкової величини (будуються точки з координатами , , ..., , ..., , де – значення випадкової величини, а – відповідні їм відносні частоти.

Таким чином, для побудови полігона частот (відносних частот), по осі абсцис відкладаємо значення варіант , а по осі ординат – відповідні частот (відносних частот ).

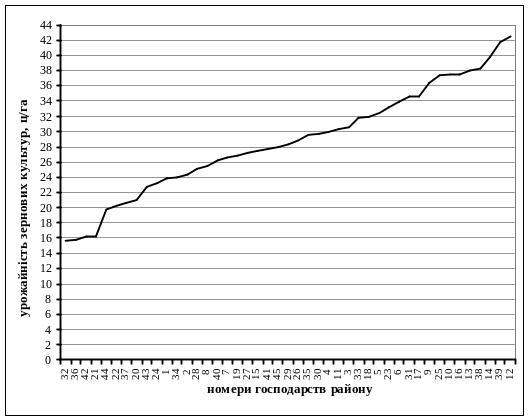
Рис. Ж.2.3. Огіва ранжированого ряду Рис. Ж.2.4. Полігон розподілу

розподілу господарств за урожайністю врожайності зернових культур

зернових культур району

Також розподіл випадкової величини за відносними частотами можна подати у вигляді полігона відносних частот, у вигляді лінійної або кругової діаграм, для останньої попередньо записавши значення відносної частоти у відсотках (частість). Побудуємо за таблицею Ж.2.5 полігон частот варіаційного ряду розподілу господарств району за урожайністю зернових культур (рис. Ж.2.4).

Якщо випадкова величина набуває багато різних значень, то її розподіл зручно графічно представити після розбиття всіх її значень на класи (інтервали, групи) так, як це робили для неперервної випадкової величини при побудові інтервального варіаційного ряду. Наочно частотний розподіл за класами (групами, інтервалами) можна теж подати за допомогою полігона частот або стовпчатої діаграми, хоча всі вище перераховані графічні об’єкти будували для дискретного варіаціного ряду розподілу випадкових величин.

Розподіл значень неперервної випадкової величини також можна подати графічно. Для цього доречною є побудова інтервального варіаційного ряду розподілу випадкової величини.

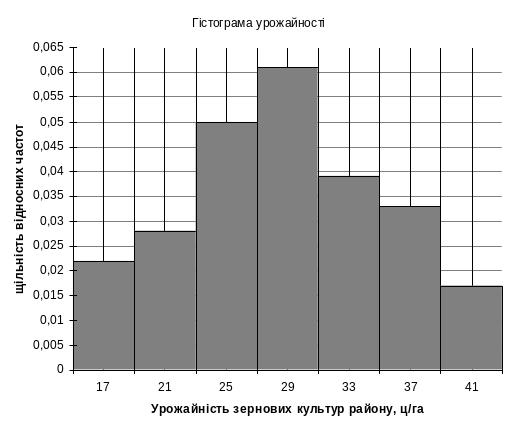
Рис. Ж.2.5. Гістограма розподілу щільності відносних частот урожайності зернових культур району

Гістограма – ступінчаста фігура, по осі абсцис якої відкладено інтервали варіаційного ряду довжиною , а висота стовпчиків відображає кількість випадків або частот у цьому інтервалі і дорівнює щільності відносних частот кожного інтервалу. Сума площ усіх прямокутників дорівнює 1. Побудуємо гістограму щільності розподілу відносних частот урожайності зернових культур району (рис. Ж.2.5).

Якщо за даними таблиці Ж.2.5 побудувати ступінчасту фігуру, висота стовпчиків якої дорівнює відносним частотам, то графічний об’єкт називатиметься гістограма відносних частот варіаційного ряду; якщо ж висота стовпців рівна частотам інтервалів – гістограма частот.

Під час побудови гістограми слід враховувати, що ширина стовпчиків однакова і рівна (пропорційна) – довжині інтервалу; стовпчики з’єднані між собою.

Проаналізувавши графічні об’єкти полігон і гістограму, легко бачити, що з графіка гістограми можна одержати полігон. Для цього слід з’єднати прямими лініями середні точки верхніх площадок гістограми. У свою чергу, гістограму можна дістати з полігона, відповідно розмістивши стовпчики. Іноді полігон і гістограму зображають в одній системі координат.

Рис. Ж.2.6. Кумулята інтервального розподілу врожайності зернових культур

району

Кумулята – графічне зображення варіаційного ряду з нагромадженими частотами (частостями). Для її побудови на осі абсцис відкладають варіанти, а на осі ординат – нагромаджені частоти (частості), які показують скільки одиниць сукупності мають значеня ознаки, що не перебільшує даного значення. Кумуляту застосовують при порівнянні різних варіаційних рядів. Для побудови кумуляти необхідні дані із таблиці Ж.2.5 третього та восьмого стовпців. В останній міститимуться накопичені частоти, утворені додаванням кожної наступної до попередньої ( ; ; ; …; ), вони визначають кількість значень ознаки, менших деякого данного числа.

Із графіка кумуляти (рис. Ж.2.6) можна визначити скільки господарств району має урожійність меншу 15 ц/га або більшу 43 ц/га – ніодного. Аналогічним чином, кількість господарств урожайність зернових яких менша 19 ц/га – не більше 9; кількість господарств рійону, урожайність яких міститься в інтервалі від 23 ц/га до 31 ц /га – 18 (оскільки 36-18=18).