5. Варіаційні ряди, їх властивості

Дані, одержані в результаті проведення вимірювань чи експериментів, мають вигляд неорганізованої маси числових значень, незалежно від того чи це вибіркові дані, чи дані з генеральної сукупності. Залежно від мети експерименту та кількості об’єктів генеральної сукупності, у деяких випадках у вибірку можна включити всі її члени. Для систематизації вибірки з генеральної сукупності досліджуваної ознаки складають ряд розподілу – це ряд чисел, що характеризують розподіл одиниць досліджуваної сукупності.

Окрім ряду розподілу використовують інші способи систематизації вибіркових даних. Нехай проведено випробувань, в результаті яких дістали вибірку, що характеризується ознакою : , , ..., . Елементи вибірки , , ..., називають варіантами. Впорядкована неспадна послідовність варіант ... ... – це ранжирований ряд розподілу. Ранжирований ряд не дає загальної картини розподілу, оскільки невидно закономірності, закладеної в ньому та величини, навколо якої концентруються варіати. Виникає необхідність подальшого узагальнення статистичних даних.

Кількісні значення ознаки, що спостерігається при відборі – це випадкова величина, із можливими значеннями , , ..., , ..., , де , 2, ..., – номер суб’єкта вибірки. Варіанти можуть приймати як дискретні (цілі числа), так і неперервні (будь-які числа, у тому числі дробові) значення, залежно від характеру варіювання.

Кількість одиниць сукупності, що мають однакове числове значення ознаки , називається частотою даної варіанти, що позначається . Частоти вказують на кількість повторень того чи іншого варіанта у вибірці. Якщо серед спостережень значення спостерігалось разів, значення – раз і т.д., значення – раз, причому ... , то число називається статистичною ймовірністю або відносною частотою події .

Дискретними називаються такі кількісні ознаки, що можуть набувати тільки перервні (цілочисельні) значення. Наприклад, число членів сім’ї, кількість верстатів, автомобілів, вміст лейкоцитів та гемоглобіну в крові тварин, тощо.

Таблиця Ж.2.1

Розподіл дискретної ознаки

номер	1	2	3	4	5	6	7	8	9	Всього
	4	5	6	7	8	9	10	11	12	572 поросят
	3	4	6	11	15	14	8	7	2	70 свиноматок

Прикладом представлення розподілу дискретної ознаки є таблиця (таблиця Ж.2.1) в яку занесено результати обстеження 70 свиноматок за кількістю народжених кожною з них поросят, де ( ) – кількість свиноматок, які народили відповідну кількість поросят ( ).

Кількісні ознаки, що можуть у певних межах набувати будь-які числові значення, називаються неперервними. Наприклад, вік, стаж роботи, урожайність, собівартість продукції, тиск, температура і т.п. Представимо розподіл із неперервно варіюючою кількісною ознакою у вигляді таблиці (таблиця Ж.2.2) вимірювання довжини 50 колосків ячменю сорту “Московський 121”.

Таблиця Ж.2.2

Розподіл неперервної ознаки

Довжина колоска, см	6-8	8-10	10-12	12-14	14-16	16-18	Всього колосків
частота	6	12	17	10	4	1	50

Як бачимо, залежно від того, дискретно чи неперервно, у вузькому чи широкому інтервалі змінюється ознака, матимемо безінтервальні та інтервальні статистичні ряди розподілу відповідно.

У безінтервальному ряді частота відноситься до конкретних значень ознаки , а в інтервальному – до окремих інтервалів (класів, груп), на які розбивається значення ознаки у межах від до .

Як бачимо з прикладу вимірювання довжини колосків ячменю сорту “Московський 121” (таблиця Ж.2.2), для неперервної варіюючої кількісної ознаки, інтервал її зміни розбивають на менші частинні інтервали, рівної (однакової) довжини. Кількість таких інтервалів (класів, груп) обчислюється за формулою Стерджеса: , де – об’єм вибірки або (дуже наближено) , де – обов’язково ціле число.

Довжина інтервалів визначається як: , де різниця – розмах вибірки – різниця між найбільшим та найменшим значенням випадкової величини у вибірці.

Середина інтервалів визначається як середнє арифметичне початкового й кінцевого числових значень інтервалів: .

Таким чином, варіаційний ряд розподілу – впорядкована статистична сукупність, представлена у вигляді таблиці, в першому рядку якої розташовані значення варіант у зростаючій послідовності, а в наступному – значення для кожної варіанти відповідних частот, сума яких дорівнює об’єму вибірки (або відносних частот, сума яких – 1).

Інтервальний варіаційний ряд – впорядкована статистична сукупність, представлена у вигляді таблиці, в першому рядку якої інтервали (класи, групи) значень, розташовані в порядку зростання, а в наступному – значення для кожного інтервалу відповідних частот, що обчислюються як сума частот кожної варіанти, що входить в інтервал (або відносних частот). Оскільки значення кінця попереднього та початку наступного інтервалів співпадають, то зазвичай, щоб варіант входив один раз до відповідного інтервалу, домовляються лівий кінець включати, а правий ні (або навпаки, залежно від мети експерименту).

Із варіаційного ряду будується кумулятивний (накопичуючий) ряд шляхом послідовного додавання частот: до частоти першого варіанта або інтервалу додається частота другого варіанта або інтервалу, до одержаної суми додають частоту третього варіанта або інтервалу і т.д. Із комулятивних рядів визначають кількість об’єктів, значення ознаки яких не перевищують задане значення.Наведемо приклад послідовної побудови інтервального варіаційного ряду. Маємо статистичні дані врожайності зернових культур господарств району (таблиця Ж.2.3).

Таблиця Ж.2.3

Дані урожайності зернових культур господарств району

Номер господар-ства	Урожайність зернових культур, ц/га	Номер господарства	Урожайність зернових культур, ц/га	Номер господарства	Урожайність зернових культур, ц/га
1	25,1	16	39,8	31	37,5
2	26,2	17	37,5	32	15,7
3	32,4	18	34,6	33	34,7
4	30,6	19	28,0	34	25,5
5	36,4	20	21,0	35	30,0
6	23,9	21	16,2	36	15,8
7	27,5	22	20,3	37	20,6
8	26,8	23	37,4	38	24,3
9	38,0	24	23,2	39	41,8
10	33,9	25	38,3	40	27,2
11	31,8	26	29,7	41	33,2
12	42,5	27	32,0	42	16,1
13	24,0	28	26,6	43	22,8
14	27,7	29	29,6	44	19,8
15	28,4	30	30,3	45	28,8

На основі аналізу даних таблиці робимо висновок, що маємо справу з неперервною варіюючою ознакою, об’ємом . За даними таблиці Ж.2.3 складемо ранжирований ряд розподілу (таблиця Ж.2.4).

На основі ранжированого ряду розподілу визначаємо найменший та найбільший варіанти: ; , тоді розмах вибірки: = =26,8. Оскільки варіююча ознака неперервна, складемо інтервальний варіаційний ряд розподілу врожайності зернових культур району.

Для цього визначимо кількість інтервалів: за формулою Стерджеса: = (або ). Довжина інтервалів: . Ми заокруглили числове значення довжини інтервалів для зручності обчислень. Це можливо за умови, що всі дані вибірки потраплять у інтервальний варіаційний ряд розподілу.

У цьому прикладі, межі інтервалів розширяться від 15 до 43, що повністю накриває вибіркові дані. (Іноді, з метою виявлення зміни ознаки за межами і кількість класів збільшують на один, зсуваючи на півширини інтервалу вліво і вправо відповідно, тобто , а ). В залежності від мети дослідження, користуються розширеною таблицею розподілу випадкової величини, включаючи до неї розподіл розглянутої величини за частотами та за відносними частотами: . Враховуючи, що законом великих чисел при значній кількості експрериментів значення відносних частот близькі до відповідних імовірностей, тому позначаємо відносні частоти як: . Іноді стовпчик з відносними частотами до таблиці не включають, замість нього записують стовпчик (рядок) із значеннями відносної частоти, вираженої у відсотках, частості: .

Для контролю правильності заповнення такої таблиці використовують те, що сума відносних частот (як і сума відповідних імовірностей) дорівнює одиниці, у відсотках 100%, а сума частот повинна дорівнювати кількості експериментів.

Аналогічним чином міркуємо щодо включення в таблицю сьомого та восьмого стовпчиків: щільності відносних частот та нагромаджених частот .

Таблиця Ж.2.4:

Ранжирований ряд господарств району за рівнем урожайності зернових культур

Номер господарства	Урожайність зернових культур, ц/га	Номер господарства	Урожайність зернових культур, ц/га	Номер господарства	Урожайність зернових культур, ц/га
32	15,7	40	27,2	18	34,6
36	15,8	7	27,5	5	36,4
42	16,1	19	28,0	23	37,4
21	16,2	27	32,0	6	23,9
44	19,8	15	28,4	31	37,5
22	20,3	41	33,2	17	37,5
37	20,6	45	28,8	9	38
20	21,0	29	29,6	25	38,3
43	22,8	26	29,7	10	33,9
24	23,2	35	30,0	16	39,8
1	25,1	30	30,3	13	24,0
34	25,5	4	30,6	38	24,3
2	26,2	11	31,8	14	27,7
28	26,6	3	32,4	39	41,8
8	26,8	33	34,7	12	42,5

Таким чином, таблиця, що містить всі перераховані вище складові має вигляд, представлений у таблиці Ж.2.5, що є інтервальним варіаційним рядом урожайності зернових культур району.

Таким чином, у таблиці Ж.2.5 перший, другий та третій стовпчики – це складові ранжированого ряду. Якщо крім трьох перерахованих стовпчиків розглядається ще й четвертий, то маємо справу з інтервальним варіаційним рядом розподілу.

Залежно від умов експерименту, п’ятий, шостий і сьомий стовпчики таблиці можуть входити до складу інтервального варіаційного ряду, а можуть і ні. Їх наявність, обумовлена умовою для побудови графічних об’єктів. Останній стовпчик таблиці у поєднанні з першими чотирма – складові кумулятивного ряду.

Отже, в залежності від умов завдання та мети дослідження, таблиця статистичного розподілу має більшу чи меншу кількість складових.

Основні властивості статистичних рядів розподілу:

1. сума відповідних частот варіант або інтервалів дорівнює об’єму вибірки: ;

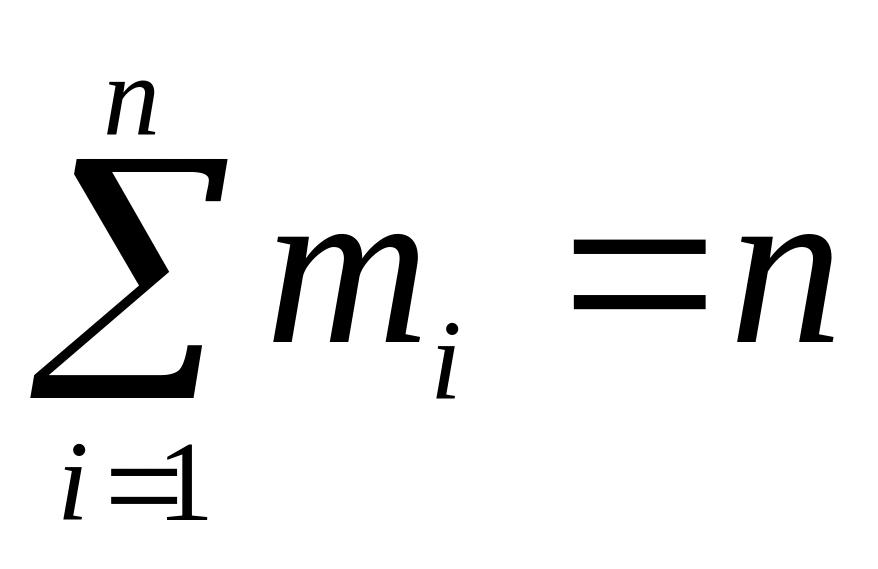2. сума відносних частот дорівнює одиниці: ;

3. сума частостей дорівнює 100%: ;

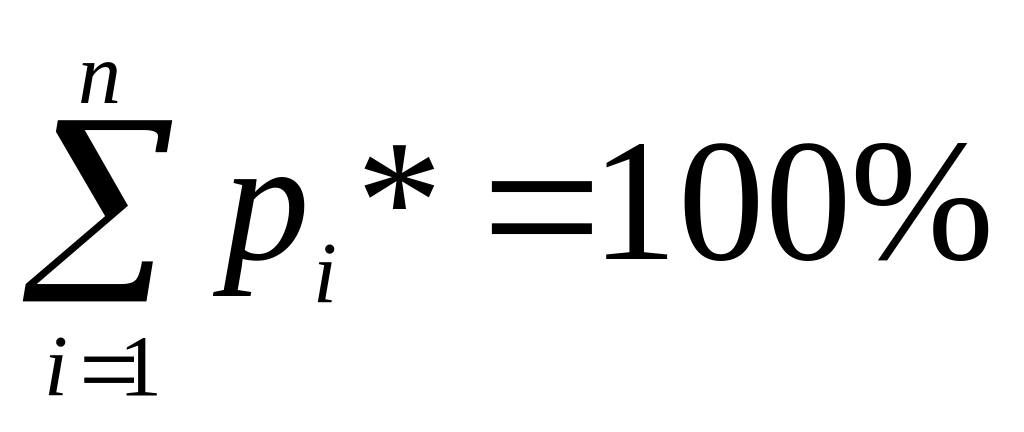4. останнє число в стовпчику нагромаджених частот дорівнює об’єму вибірки: .

Таблиця Ж.2.5

Інтервальний варіаційний ряд урожайності зерновиз культур району

Номер інтервалу	Інтер-валу,	Середина інтервалу,	Частота, mi	Відно-сна частота,	Частість,	Щіль-ність відно-сних частот,	Нагрома-джена частота,
1	2	3	4	5	6	7	8
1	[15-19)	17	4	0,09	9	0,022	4
2	[19-23)	21	5	0,11	11	0,028	9
3	[23-27)	25	9	0,20	20	0,050	18
4	[27-31)	29	11	0,24	24	0,061	29
5	[31-35)	33	7	0,16	16	0,039	36
6	[35-39)	37	6	0,13	13	0,033	42
7	[39-43)	41	3	0,07	7	0,017	45
сума			45	1,00	100

Враховуючи властивості статистичних рядів розподілу ми маємо можливість постійно здійснювати контроль за правильністю й точністю обчислень.