2.2. Формула полной вероятности. Формула Бейеса Решение типовых задач
Прибор может работать в трех режимах: нормальном, форсированном и недогруженном. Нормальный режим наблюдается в 60% случаев работы прибора, форсированный - в 30% и недогруженный - в 10%. Надежность прибора (вероятность безотказной работы в течение заданного времени t) для нормального режима равна 0,8; для форсированного - 0,5; для недогруженного - 0,9. Найти полную (с учетом случайных условий) надежность прибора.
Сформулируем три гипотезы:
H1- нормальный режим;
H2- форсированный режим;
H3- недогруженный режим.
Пусть событие А - безотказная работа прибора. При введенных обозначениях данные задачи можно записать так:
;
;
;
;
;
.
Тогда, по формуле полной вероятности:
.
▲
Имеется три одинаковых ящика. В первом ящике находятся 5 стандартных и 4 бракованных детали, во втором - 8 стандартных и 2 бракованных, в третьем - 5 стандартных и 5 бракованных. Какова вероятность того, что из наугад выбранного ящика наудачу взятые 3 детали окажутся стандартными.
Имеем 3 гипотезы:
H1 - выбор первого ящика;
H2 - выбор второго ящика;
H3 - выбор третьего ящика.
Т.к. гипотезы по условию равновозможные, то
.
Пусть событие А
состоит в том, что три детали, выбранные
из определенного ящика, окажутся
стандартными. Т.к. в первом ящике
содержится 10 деталей, то 3 детали можно
выбрать числом способов
,
из этих способов событию А
благоприятствуют m
способов, где
.
По классическому определению вероятности
.
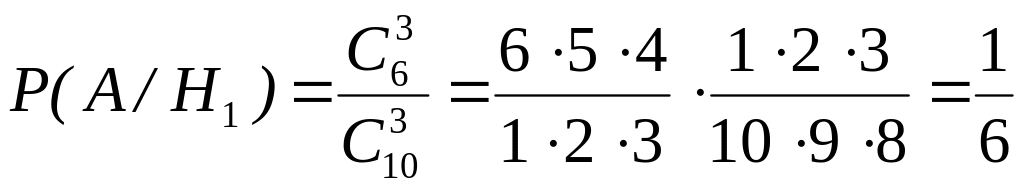Аналогично находим
для второго ящика:
,
;
.
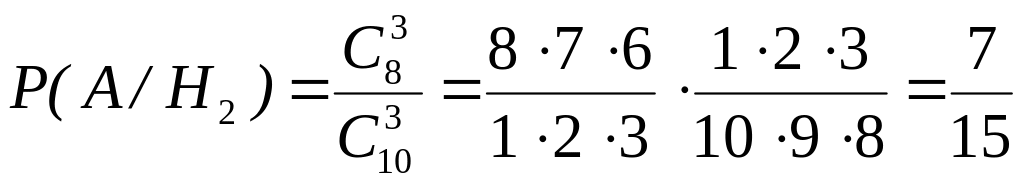Для третьего ящика:
.
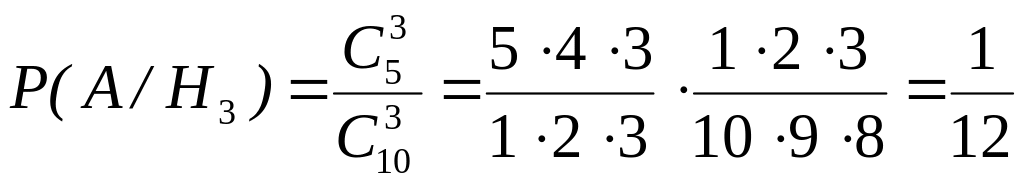По формуле полной вероятности
.
▲
В условии предыдущей задачи, считая известным, что выбранные три детали оказались стандартными, найти вероятность того, что они были взяты из второго ящика.
Можем воспользоваться формулой Бейеса:
.
▲
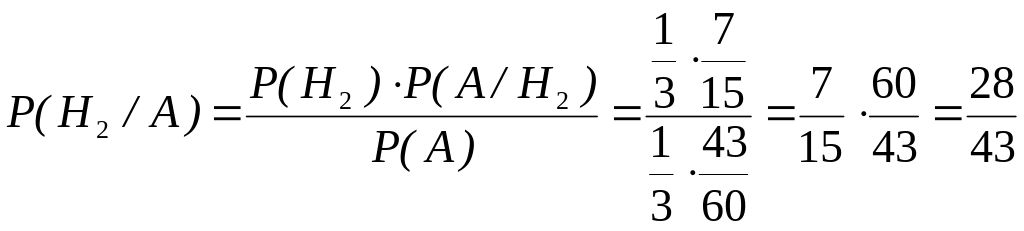Стрельба подводной лодки по береговому объекту может произойти с одной из трех позиций, вероятности выхода на которые равны соответственно 0,2; 0,3 и 0,5. Вероятности поражения цели с данных позиций равны соответственно 1; 0,75 и 0,4. Произведена стрельба, в результате которой цель поражена. С какой позиции вероятнее всего произведена стрельба?
Пусть событие А - поражение цели. Событие А может произойти только с одной из трех гипотез:
H1 - выход на первую позицию;
H2 - выход на вторую позицию;
H3 - выход на третью позицию.
Найдем вероятность каждой гипотезы по формуле Бейеса. Для этого найдем предварительно полную вероятность события А:
.
;
;
.
Мы видим, что наибольшей является вторая дробь, т.е. вероятнее всего, что стрельба производилась со второй позиции. ▲