§ 1.Основные понятия теории вероятностей. Решение типовых задач.

1.1. В урне находится 10 шаров одинакового диаметра: 2 красных, 3 белых и 5 синих. Найти вероятность того, что вынутый наугад шар будет белым.

Пусть - событие, состоящее в том, что вынут белый шар. Ясно, что - число всех равновозможных исходов опытов (шары одинакового размера, и их цвет не виден при выемке). Они несовместны и образуют полную группу. Число случаев, благоприятствующих событию , равно 3, т.е. . Следовательно, по формуле (1.1) имеем:

, т.е. ▲

1.2. Набирая номер телефона, абонент забыл одну цифру и набрал ее наугад. Найти вероятность того, что набрана нужная цифра.

Пусть - событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому – число всех равновозможных исходов опыта. Они несовместны и образуют полную группу. Благоприятствует событию лишь один исход (нужная цифра лишь одна). Следовательно, по формуле (1.1) имеем:

. ▲

1.3. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Обозначим через событие «набраны две нужные цифры». Здесь - общее число всех равновозможных исходов опыта. Эти исходы несовместны и образуют полную группу. Благоприятствует событию лишь один исход, т.е. тогда

. ▲

1.4. В партии из 20 однотипных деталей 15 стандартных. Найти вероятность того, что среди выбранных наугад для проверки шести деталей четыре окажутся стандартными.

Пусть - событие, состоящее в том, что среди выбранных наугад для проверки шести деталей четыре окажутся стандартными. Выбрать 6 деталей из 20 можно способами. Определим число случаев, благоприятствующих событию . Нам требуется выбрать 4 стандартные детали из 15 имеющихся стандартных, что можно сделать способами, и 2 нестандартных, которые берутся из 5 имеющихся нестандартных, что можно сделать способами. Следовательно, по основному правилу комбинаторики (правилу умножения) имеем:

Следовательно, по формуле (1.1) имеем:

. ▲

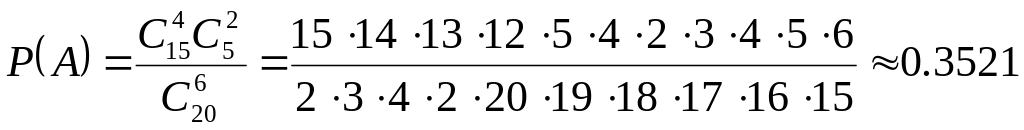1.5. В составе группы из 7 самолетов находится 2 самолета-носителя атомного заряда. Места их в группе произвольны. Система ПВО сбила 5 самолетов. Какова вероятность того, что среди этих 5 самолетов находятся оба носителя атомного заряда? Какова вероятность того, что в числе сбитых самолетов будет один самолет-носитель?

Пусть событие - среди 5 сбитых самолетов находятся 2 самолета-носителя атомного заряда. Событие - в число сбитых самолетов попал 1 самолет-носитель. Т.к. по условию задачи сбито 5 самолетов, то каждый исход опыта представляет собой выбор 5 произвольных самолетов из данных. Т.к. мы рассматриваем группу из 5 самолетов, отличающиеся друг от друга хотя бы одним самолетом, то речь идет о сочетаниях, т.е.

.

Подсчитаем число исходов, благоприятствующих событию – в числе сбитых оба самолета-носителя. Чтобы составить группу из 5 самолетов, содержащую 2 самолета-носителя, нужно выбрать 3 самолета - неносителя из имеющихся 5 таких самолетов, что можно сделать числом способов , т.е.

.

Тогда по классическому определению вероятности

.

Подсчитаем число случаев, благоприятствующих событию – в числе сбитых будет один самолет-носитель. Чтобы составить группу из 5 самолетов с самолетом-носителем, нужно выбрать 1 самолет-носитель числом способов и 4 самолета - неносителя числом способов . Поэтому по основному правилу умножения

.

Тогда

. ▲

1.6. Имеются шесть карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что:

1. получится слово ЛОМ, если наугад одна за другой выбираются три карточки;

2. получится слово МОЛНИЯ, если наугад одна за другой выбираются шесть карточек и располагаются в порядке появления.

а) Из шести данных букв можно составить трехбуквенных «слов» (НИЛ, ОЛЯ, ОНИ и т.д.). Слово ЛОМ при этом появиться лишь один раз, т.е. . Поэтому вероятность появления слова ЛОМ (событие ) равно

.

б) Шестибуквенные "слова" отличаются друг от друга лишь порядком расположения букв (НОЛМИЯ, ЯНОЛИМ, ОЛНИЯМ и т.д.). Их число равно числу перестановок из 6 букв, т.е. . Очевидно, что . Тогда вероятность появления слова МОЛНИЯ (событие ) равна

. ▲

1.7. В квадрат вписан круг. Какова вероятность того, что точка, брошенная наудачу в квадрат, окажется внутри круга (рис.1.2)?

Пусть радиус круга равен R, тогда сторона квадрата 2R. Площадь круга равна , а квадрата - .

Р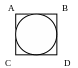 ис.1.2

По геометрическому определению, вероятность попадания точки в квадрат равна

. ▲

1.8. (Задача о встрече). Два товарища договорились встретиться в течение установленного часа в определенном месте. Пришедший первым ждет другого 15 минут, затем уходит. Какова вероятность того, что встреча состоится, если каждый выбирает момент прихода в течение установленного времени наудачу.

Р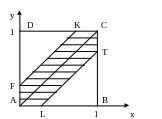 ис.1.3

Пусть - момент прихода первого товарища, а - второго. Возможные значения : , . Так как моменты прихода равновозможные в течение установленного часа, то точка с одинаковой вероятностью попадет в квадрат (рис.1.3).

Точки, лежащие на диагонали квадрата, с уравнением соответствуют одновременному появлению в условленном месте обоих товарищей. Линия с уравнением соответствует тому, что второй товарищ приходит на четверть часа позже первого. Линия с уравнением соответствует тому, что второй товарищ приходит на четверть часа раньше первого. Встреча состоится, если точка попадет в область между линиями и , т.е.

.

Последнее неравенство определяет область , заштрихованную на рис.1.3.

Условия геометрической вероятности соблюдаются, поэтому можно применить формулу (1.2).

Площадь области (площадь квадрата ) равна единице. Площадь области определяем, вычитая из площади квадрата площади двух треугольников:

.

Если - событие, заключающееся в состоявшейся встрече, то

.
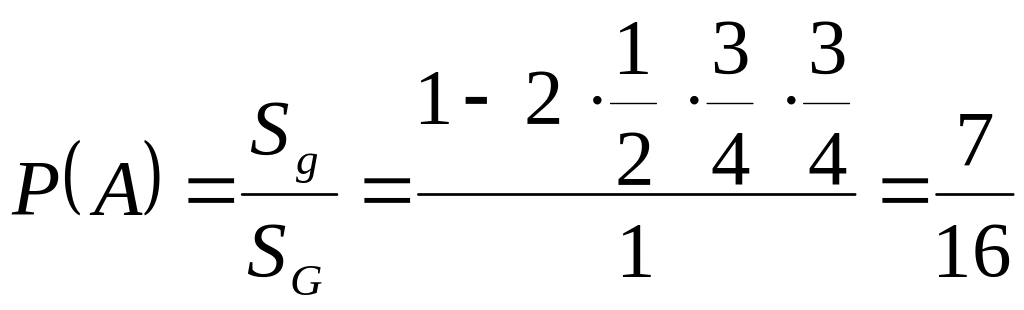