4. Влияние конфигурации заряда.

Предположим, что нанозаряд излучается неограниченной плоской стенкой толщиной 2r₀, бесконечно длинным круглым цилиндром и шаром радиуса r₀. Необходимо установить характер изменения градиента потенциала (напряженности или индукции) с расстоянием r (рис. 12). Этот вопрос имеет принципиальное значение для дальнейшего.

Рис. 12. Распределение потенциала вблизи неограниченной плоской

стенки (слева), бесконечно длинного цилиндра и шара (справа).

Согласно закону сохранения заряда, на стационарном режиме за единицу времени через любое сечение поля с координатой r (величина переменная) проходит одно и то же количество заряда. В случае плоской стенки площадь сечения F не зависит от r. Следовательно, при постоянных dЕ_нан и F градиент потенциала (dР/dх) также является величиной постоянной, не зависящей от r [формула (370)] и равной градиенту (dР/dх)₀ на поверхности (при r = r₀) заряда, т.е.

dР/dх = (dР/dх)₀ = const. (381)

В случае цилиндра площадь сечения пропорциональна радиусу:

F = 2rl м²,

где l - длина цилиндра.

Написав уравнение (370) для двух радиусов r₀ и r и приравняв величины зарядов, получим

dР/dх = (dР/dх)₀(r₀/r). (382)

В цилиндрическом поле градиент потенциала обратно пропорционален радиусу.

В случае шара

F = 4r² м².

Следовательно, градиент потенциала в точке с координатой r связан с градиентом в точке r₀ соотношением

dР/dх = (dР/dх)₀(r₀²/r²). (383)

В сферическом поле градиент потенциала обратно пропорционален квадрату радиуса. Точно таким же образом изменяется удельный поток J нанозаряда.

Природа отмеченного явления (уменьшения с расстоянием r потока J для цилиндрического и сферического полей) объясняется чисто геометрическими соображениями – возрастанием площади F с радиусом r. Одновременно убывают градиенты потенциалов, напряженности, индукции и действующие на заряд силы. Сравнение характера изменения потенциала и градиента потенциала с расстоянием r для плоского, цилиндрического и сферического полей показано на рис. 13. Потенциал быстрее всего уменьшается у плоского поля, а градиент потенциала – у сферического поля.

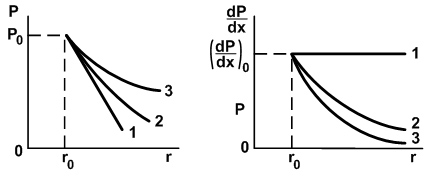
Рис. 13. Сравнение кривых распределения потенциала (слева) и градиента потенциала вблизи пластины (прямая 1), цилиндра (кривая 2) и шара (кривая 3).

Разумеется, все эти соотношения справедливы только в условиях, когда пространство обладает континуальными свойствами, т.е. при большом числе метронов, и когда поток пространства заметно не искривляется, т.е. вблизи него нет больших зарядов различного рода.

§ 42. Принцип стабильности.

1. Формулировка принципа.

При изучении конфигурации полей потенциала можно обнаружить одну особенность, которая заключается в стремлении любого поля выровняться, приобрести вдали от источника одну из рассмотренных выше простых конфигураций – плоскую, цилиндрическую или сферическую. Это свойство полей будем именовать принципом стабильности потока заряда.

Частный случай этого принципа известен в гидродинамике. В потоке вязкой жидкости вдали от входа в канал всегда устанавливается определенное распределение скоростей по сечению, не зависящее от распределения скоростей на входе. Это свойство именуется свойством стабильности потока вязкой жидкости.

В теории упругости известен также принцип Сен-Венана (1855), согласно которому замена одной системы усилий, действующих на небольшую часть поверхности упругого тела, другой, статически эквивалентной системой усилий, действующих на ту же часть поверхности тела, вызывает значительные изменения только местных напряжений, не сказываясь заметно на напряжениях в точках, достаточно удаленных от поверхности, на которой усилия были изменены.

Наконец, автором аналогичное свойство стабильности было обнаружено у температурных полей [2, 3].

В общем случае принцип стабильности справедлив для любых форм движения. Любое поле вдали от источника стремится стать одномерным – плоским, цилиндрическим или сферическим. Это стремление поля легко понять, если вспомнить, что неоднородность поля обусловлена неодинаковыми количествами заряда, содержащегося в различных участках поля. Это вызывает появление выравнивающих потоков. В результате поле становится практически одномерным. Полностью выровняться (стать однородным) ему мешает источник.

Примером может служить поле, изображенное на рис. 14. На некотором расстоянии от источников поле делается приблизительно сферическим (если источники – шары) или цилиндрическим (если источники – цилиндры).

Рис. 14. Изопотенциальные линии, расположенные вокруг двух

одноименных шаровых (или цилиндрических) зарядов.

Принцип стабильности формулируется следующим образом: если на некотором участке поверхности заряда изменить характер распределения условий излучения поля без изменения общей величины потока нанозаряда, то это практически не отразится на поле потенциала вдали от рассматриваемого участка. В частном случае условия излучения могут изменяться путем изменения конфигурации заряда или применения дискретной системы зарядов.