Параллельное соединение катушки и конденсатора

Д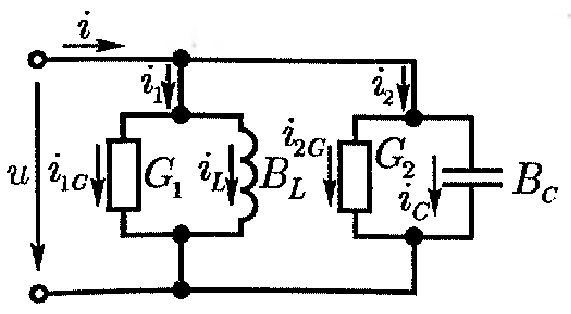 ля рассмотрения параллельного соединения катушки и кон­денсатора представим их на схеме активными и реактивными проводимостями.

Согласно первому закону Кирхгофа, мгновенная величина об­щего тока равна сумме мгновенных токов отдельных ветвей:

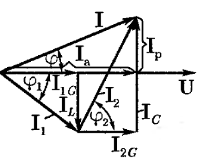
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три слу­чая.

B L>Вс. Iа = I1G+ I2G— активная составляющая; Iр = IL+IC— реактивная составляющая. G = G1+ G2 Cos  = Ia/ I; Sin  = IP/ I; Tg = (IL - IC) / IA Cos  = G / Y; Sin = B/ Y; tg = (IL - IC)/IA; .

B L<Вс.

2. B _L=В_с.

I_p=0; I=I_a

В этом случае имеет место резонанс токов.

Из векторной диаграммы токов легко получить треугольник мощностей и проводимостей которые были получены для последовательного соединения катушки и конденсатора. В соответствии с этим знак реактивной мощности (проводимости) может быть и положительный и отрицательный.

Расчет цепей с параллельным соединениемветвей

Р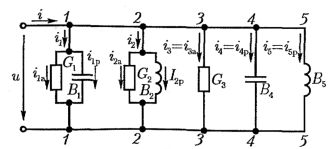 асчет электрической цепи, рассмотренный в предыдущем пара­графе, можно применить для цепей, содержащих произвольное чис­ло приемников, соединенных параллельно.

Пусть на входе электрической цепи действует синусоидальное напряжение .

Численные значения векторов токов определяются произведе­нием напряжения и проводимости соответствующей ветви.

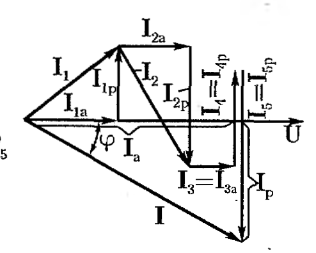
Расчет цепи без определения проводимостей ветвей

Расчет электрической цепи при параллельном соединении вет­вей можно выполнить без предварительного определения активных и реактивных проводимостей.

Для построения векторной диаграммы токов дополнительно определим ак­тивные и реактивные составляющие тока каждой ветви: ;

Символический метод

К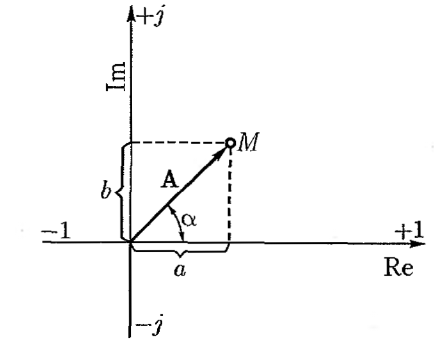 аждому вектору в ком­плексной плоскости соответствует комплексное число, которое можно выразить в алгебраической, тригонометрической, показательной формах.

алгебраическаяА = а + јb;

тригонометрическаяА = Acos𝛼 + јsin𝛼;

показательнаяА =Ae^ja.

Это дает основание от графи­ческого (векторного) выражения синусоидальных напряжений и токов перейти к аналитическому выражению их комплексными числами, а операции с векторами заменить алгебраическими действиями.

П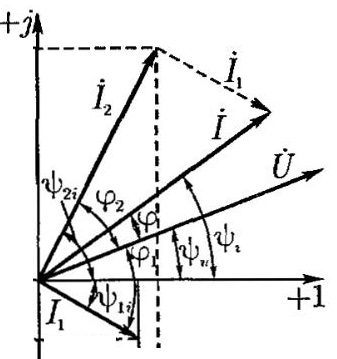 ри расчете электрических цепей переменного тока использу­ют или определяют следующие величины: ЭДС напряжения, токи, сопротивления и проводимости, мощность. Все эти величины должны быть выражены в символической форме, т. е. комплексны­ми числами.

Выражение характеристик электрических цепей комплексными числами Напряжения и токи

Комплексы синусоидально изменяющихся величин принято отмечать точками над их буквенными обозначениями (например, комплексы напряженияŮ, тока İ). Комплексы величин, не зависящих от времени (например, сопротивлений, проводимостей), обозначают большими буквами без точек, но с черточкой внизу:Z,Y.

Э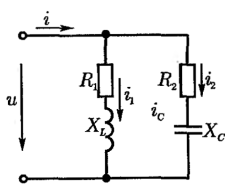 тому напряжению соответствуют вектор Uв комплексной плоскости и комплексное число в показательной форме

Ů= U

Ток i₁в катушке отстает от напряжения на угол ₁

Вектору тока I₁соответствует комплексное число

İ₁=I₁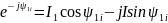

Ток в конденсаторе опережает напряжение на угол ₂.

;

İ₂=I₂

İ= İ₁+İ₂ по правилу параллелограмма

Сложение этих векторов в других формах

İ + (

I

Действительная и мнимая части комплекса тока равны проекци­ям вектора тока на оси комплексной плоскости.

Действительная и мнимая части комплекса тока равны соответственно активной и реактивной составляющим век­тора тока только в том случае, если вектор напряжения направлен вдоль оси действительных чисел, т.е. комплекс напряжения выра­жается действительным числом.