Р асчет несимметричной трехфазной цепи при соединении источника и приемника звездой

Рассмотрим сначала общий случай расчета цепи с нулевым про­водом, сопротивление которогоZ_N.При этом сделаем некоторые уп­рощения: сопротивления линейных проводов и фаз источников бу­дем полагать равными нулю. Если указанные сопротивления нель­зя считать равными нулю, их можно отнести к приемнику, приба­вив к сопротивлениям последнего по правилам сложения комплек­сов.

При таком упрощении потенциалы линейных зажимов источ­ника и приемника можно считать одина­ковыми. Тогда напряжения между нулевыми точками N и N'определится по формуле:

Напряжения на фазах приемника:

Т оки в фазах:

Ток в нулевом проводе:

Для узловой точки N илиN'справедливо также уравнение по первому закону Кирхгофа:

Смещение нейтрали

При наличии сопротивления в нулевом проводе (Z_N≠0) нуле­вая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжениеU_Nназывают на­пряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодина­ковыми, несмотря на симметрию фазных напряжений источника.

Электрические цепи с несинусоидальными напряжениями и токами

Несинусоидальные периодические функции, так же как и сину­соидальные, наглядно изображаются в виде графиков. Для расче­тов требуются аналитические выражения несинусоидальных функций.

Ряды Фурье

Аналитическое выражение несинусоидальной периодической функции осуществляется с помощью теоремы Фурье, согласно ко­торой любая периодическая функция может быть представле­на в виде суммы ряда составляющих, из которых одна составляю­щая постоянная, а другие являются синусоидальными функциями с кратными частотами (в дальнейшем они называются гармониче­скими составляющими или просто гармониками): .

постоянная составляющая (амплитуды гармонических составляющих).

начальные фазы гармоник.

Первая гармоническая составляющая имеет период, равный пе­риоду несинусоидальной кривой .Она называется первой, или основной, гармоникой.

Все другие гармонические составляющие имеют частоты, в це­лое число раз больше частоты первой гармоники. Эти гармоники называют высшими.

Данную формулу можно преобразовать применив формулу синуса суммы двух углов:

Применяя подобную запись ко всем гармоническим составляю­щим, несинусоидальную функцию можно выразить так:

Функция, симметричная относительно оси абсцисс (х)

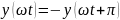
При симметрии относительно оси абсцисс значения функции повторяются с обратным знаком через половину периода, поэтому отрицательная полуволна, сдви­нутая на половину периода, явля­ется зеркальным отображением положительной полуволны. Такую форму имеет кривая тока в катушке с ферро­магнитным сердечником при си­нусоидальном напряжении.

В составе тригонометрической функцииотсутству­ют постоянная составляющая и гармонические четного порядка.

Функция, симметричная относительно оси ординат (у)

Функция, симметричная от­носительно оси ординат, не со­держит синусов:

Входящие в со­став ряда косинусы сим­метричны относительно оси ординат, а синусы несимметричны. Ес­ли функция в целом симметрична относительно оси ординат, то это возможно лишь при отсутствии синусов.