Синусоидальный ток и эдс

П ериодический электрический ток, являющийся синусоидальной функцией времени, называется синусоидальным электрическим током.

При равномерном вращении ротора в его обмотке наводится ЭДС. Если обмотку генератора замкнуть через сопротивление, то в об­разовавшейся цепи возникает синусоидальный ток, повторяющий по форме кривую ЭДС.

Пусть сопротивление цепи равнымR, получим для тока такое выражение:

Уравнение и графики синусоидальных величин

П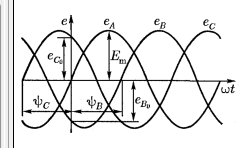 ри вращении ротора ЭДС бу­дет наводиться во всех витках, но уравнения ЭДС не будут одина­ковыми. Эта зависимость ЭДС от начального положения витка учитыва­ется введением в уравнение начального угла.

В общем виде уравнение ЭДС должно быть запи­сано так:

е = Е_тsin (𝜔t+ ψ)

отстают по фазе

Характеристики синусоидальных величин

У равнением и графиком зада­ются все характеристики сину­соидально изменяющейся вели­чины: амплитуда, угловая часто­та, начальная фаза, период, час­тота и для любого момента вре­мени мгновенная величина.

Дадим определения, которые распространяются на все величины, изменяющиеся по синусоидальному закону (ток, на­пряжение и др.).

Мгновенная величина (или мгновенное значение) ЭДС — величина ЭДС в рассматриваемый момент времени.

Период Т— наименьший интервал времени, по истечении ко­торого мгновенные величины периодической ЭДС повторяются.

Частота — величина, обратная периоду: ƒ= 1/Т.

Амплитуда Е_т — наибольшая величина, которую принимает ЭДС в течение периода. Амплитуда является одной из мгновенных величин, которая соответствует аргументу 𝜔t± ψ.

Фаза (фазовый угол𝜔t± ψ) — аргумент синусоидальной ЭДС, отсчитываемый от ближайшей предшествующей точки перехода ЭДС через нуль к положительному значению.

Начальная фаза ψ— фаза синусоидальной ЭДС в начальный мо­мент времени.

Две синусоидальные величины, имеющие разные начальные фа­зы, называются сдвинутыми по фазе.

Угловая частота 𝜔, или угловая скорость, характеризуется углом поворота ротора генератора в единицу времени.

Векторной диаграммы

В еличины, изменяющиеся по синусоидальному закону, задавали уравнениями и изображали графиками в прямоугольной системе координат. При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин с помощью вращающихся векторов.

При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против враще­ния часовой стрелки, а отрицательные — по ее движению.

Совокупность векторов, изображающих на одном чертеже не­сколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.

М_и = 50 В/см; M_i= 4 А/см

Сложение и вычитание векторов

П ростота и наглядность векторных диаграмм главное достоинство способа изображения синусоидальных ве­личин.

Путь имеется два тока заданные уравнениями:

Сложение трёх векторов удобнее вести в та­ком порядке: один вектор остается на месте, другие переносятся параллельно самим себе так, чтобы начало последующего вектора сов­пало с концом предыдущего.

В ычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) с вычитаемым вектором, поверну­тым на 180°.