12.4.3. Связь между поляризованностью и напряжённостью поля

Установим теперь связь между поляризованностью и напряжённостью поля внутри диэлектрика. Наиболее просто эту связь можно найти на примере неполярного диэлектрика. Каждая молекула такого диэлектрика, находясь во внешнем электростатическом поле, приобретает дипольный момент, определяемый формулой (2.3). Дипольные моменты неполярных молекул параллельны вектору , поэтому суммарный момент , где N – число молекул в объёме V. На основании (12.3) , поэтому , где n – число молекул в единице объёма вещества. Обозначим n, тогда ,(2.10)

Параметр  в (2.10) называется диэлектрической восприимчивостью и характеризует «податливость» вещества к поляризации: чем больше , тем больше при данном значении напряжённости поля E поляризованность диэлектрика P.

Для не слишком сильных полей формула (2.10) справедлива также и для полярных диэлектриков. Действительно, по мере возрастания внешнего электрического поля будет возрастать и степень ориентации дипольных молекул (среднее значение cos). Можно показать, что в этом случае диэлектрическая восприимчивость

,

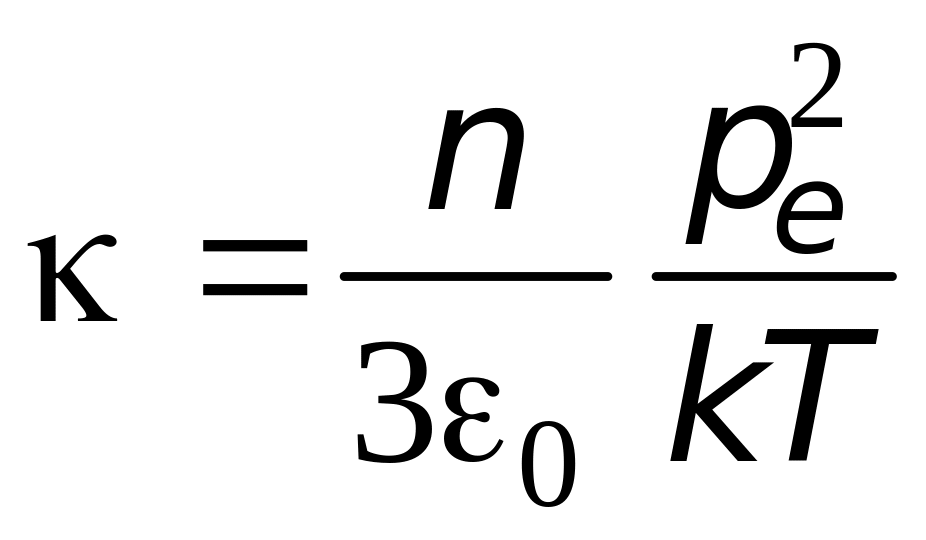где n – концентрация молекул; k – постоянная Больцмана.

Таким образом, в отличие от неполярных диэлектриков, диэлектрическая восприимчивость полярных диэлектриков падает с ростом температуры.

12.4.4. Вектор электрического смещения

Напряжённость электрического поля, являющаяся его силовой характеристикой, зависит от среды, в которой создано поле. Введём теперь иную характеристику электростатического поля, величина которой не зависит от среды – вектор электрического смещения

.

(2.11)

Поскольку , то, как видно из (2.11), D не зависит от . Пример: поле точечного заряда

.

Вектор не зависит от свойств среды и характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме) при таком же их распределении в пространстве, которое имеется при наличии диэлектрика.

Суммарное электростатическое поле в диэлектрике представляет собой наложение двух полей: внешнего поля и направленного ему навстречу поля связанных зарядов, величина которого зависит от свойств диэлектрика.

12.4.5. Связь между векторами , и .

Для установления этой связи рассмотрим электростатическое поле в плоском конденсаторе в отсутствие и при наличии диэлектрика между его обкладками.

Рис. 2.6

Пусть конденсатор заряжен и плотность свободных зарядов на его обкладках равна  (рис 2.6, а). Если в пространстве между обкладками конденсатора вакуум, то согласно (1.15) .Однако из (12.11) при 1 (вакуум) следует .Введём теперь внутрь конденсатора диэлектрик (рис. 2.6, б). В результате поляризации диэлектрика на его внешних поверхностях образуются связанные заряды с поверхностной плотностью , которые создаю внутреннее электростатическое поле противоположного направления ,или с учетом (2.9) , (2.13)

Очевидно, что результирующая напряжённости поля в диэлектрике .(2.14)

Подставим в (2.14) выражения (12.12) и (12.13), получим .(2.15)

И наконец, подставив в (2.15) выражение (2.9) и (2.11), получим связь между диэлектрической проницаемостью  и диэлектрической восприимчивостью : , (2.16)