2.2. Полярные и неполярные молекулы

Молекула электрически нейтральна: положительные заряды ядер полностью компенсируются отрицательным зарядом электронов, но несмотря на это молекулы “чувствуют” воздействие со стороны внешнего электрического поля.

Для рассмотрения механизма этого воздействия введём такие понятия, как положительных и отрицательных зарядов.

Пусть в некоторой системе координат положение i-го положительного заряда задаётся радиусом-вектором . Тогда центр положительных зарядов определяется как

,

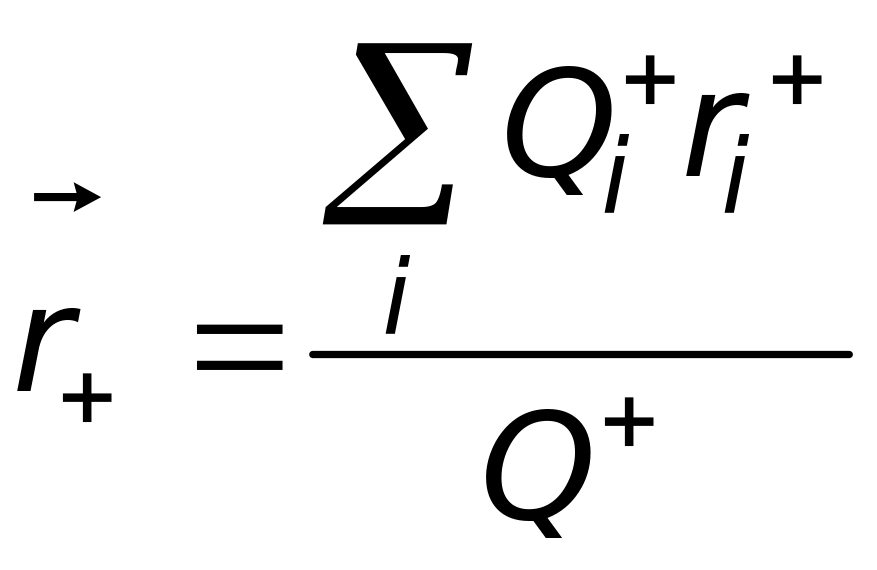(2.1)

где – суммарный положительный заряд молекулы.

Заметим, что центр положительных зарядов определяется точно так же, как и цент масс материальных точек (формула (2.9)). Центр отрицательных зарядов определятся аналогично:

,

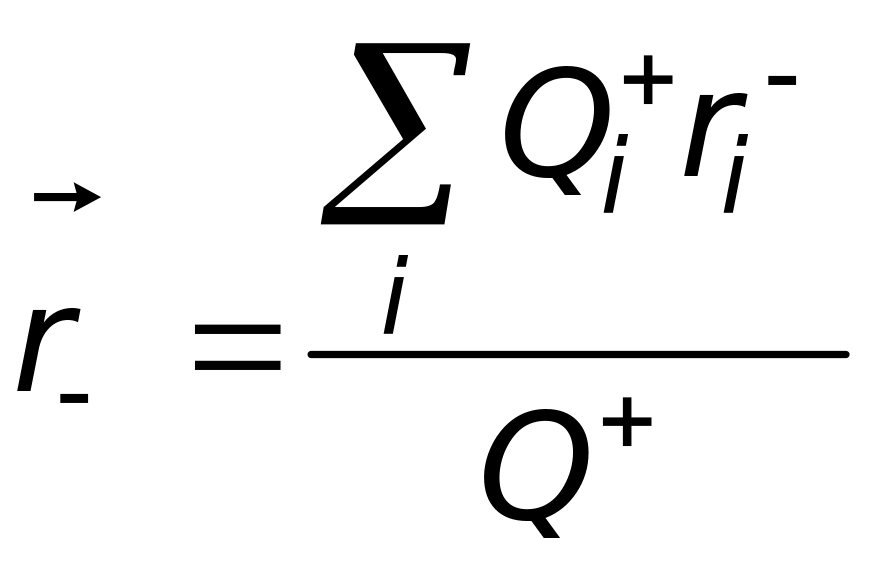(2.2)

где – суммарный отрицательный заряд молекулы. Так как молекула электрически нейтральна, то Q⁺Q^-=Q. При этом, однако, может оказаться, что центры положительных и отрицательных зарядов не совпадают (r₊r_-), т.е. молекулу можно рассматривать как электрический диполь с плечом l__ Дипольный момент молекулы . Молекулы с отличным от нуля дипольным моментом называются полярными. Типичными полярными молекулами являются соединения атомов первой и седьмой групп. Например, в молекуле HCl электрон атома водорода захватывается хлором – в результате центр положительных зарядов находится вблизи иона H⁺, а отрицательных – вблизи иона Cl^–.

У неполярных молекул центры положительных и отрицательных зарядов совпадают: r₊=r_–. Дипольный момент неполярных молекул в отсутствие внешнего электрического поля равен нулю. Примером неполярных молекул являются атомарный водород, гелий, симметричные молекулы типа H₂, O₂, бензол и т.д.

Рассмотрим теперь поведение неполярных и полярных молекул во внешнем электростатическом поле.

2.2.1. Неполярная молекула во внешнем электростатическом поле

В отсутствие внешнего электростатического поля центры положительных и отрицательных зарядов неполярной молекулы совпадают (рис. 2.1, а). При наложении поля на положительные и отрицательные заряды молекулы действуют противоположные по направлению силы. Под действием этих сил центры положительные и отрицательных зарядов смещаются на расстояние x (рис. 2.1, б). Как показывают теория и опыт, в относительно слабых полях смещение x пропорционально напряженности поля E: x~E. Следовательно, p_l=Qx~E. Эту пропорциональную зависимость можно записать в виде равенства

,

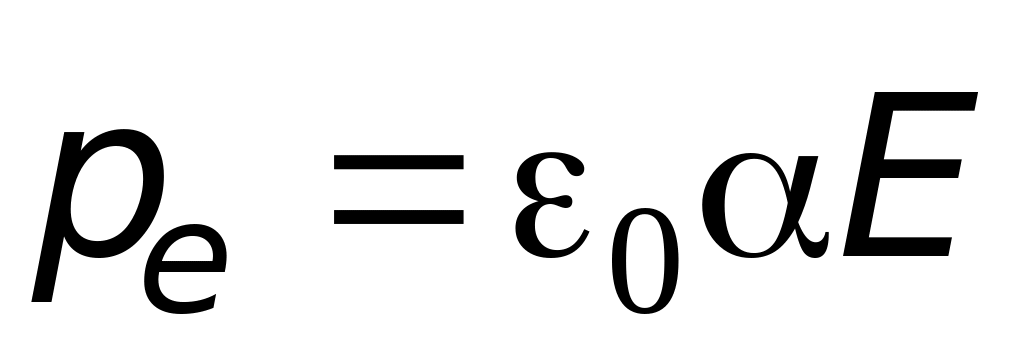(2.3)

Рис. 2.1

где  – поляризуемость молекулы. Этот параметр для различных молекул разный: чем больше , тем больший дипольный момент приобретает молекула в электростатическом поле с определенным значением вектора напряженности.

2.2.2. Полярная молекула во внешнем электростатическом поле

Как было указано, каждая полярная молекула обладает собственным (жестким) дипольным моментом. Пусть первоначально диполь ориентирован под углом  к направлению вектора (рис. 2.2). При этом на него будет действовать пара сил, создающая вращательный момент

,

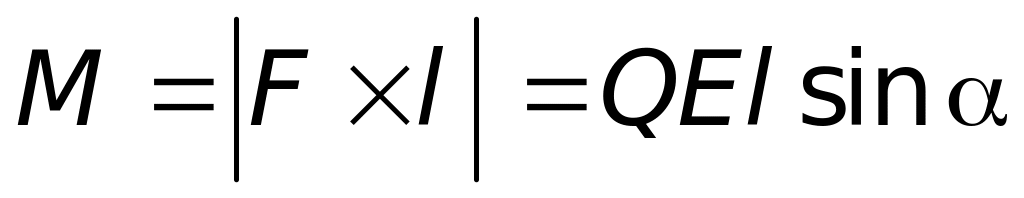(2.4)

и диполь будет проворачиваться до тех пор, пока вектор дипольного момента p_e не станет параллельным вектору напряженности ¹.

Рис. 2.2

Найдем потенциальную энергию диполя как сумму энергии зарядов +Q и -Q.

,

где W₁=-Q_, W₂=Q_ – энергия зарядов -Q и +Q, находящихся в точках поля с потенциалами соответственно _ и _ на рис. 2.2 эквипотенциальные поверхности _=const и _=const (показаны пунктиром). Таким образом,

.

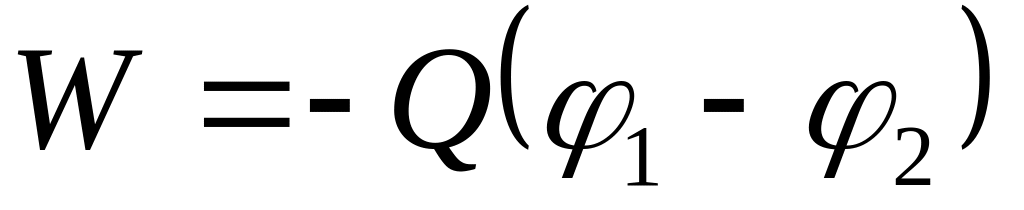(2.5)

Используя (11.37) и замечая, что d=lcos φ (рис. 12.2) из (12.5) получаем

.

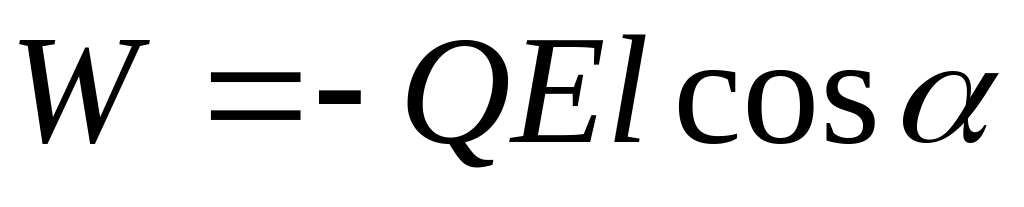Поскольку произведение заряда Q на плечо диполя l есть дипольный момент p_e, то

.

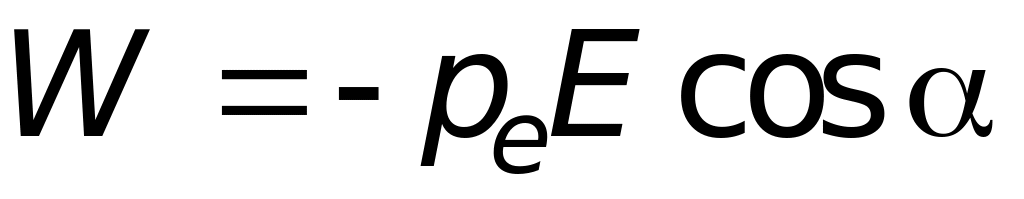(2.6)

или

.

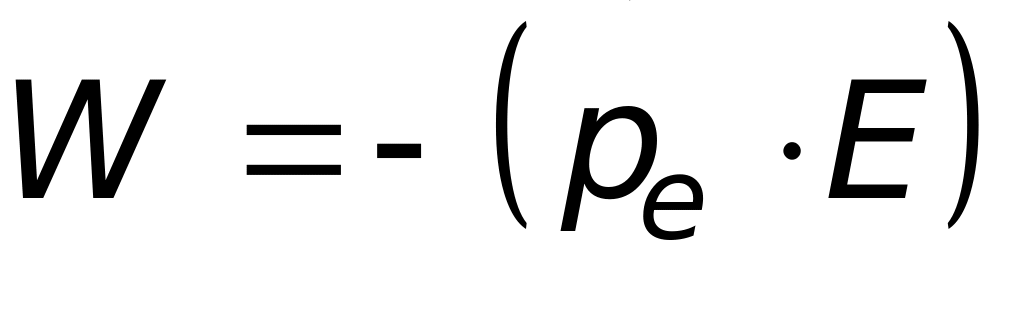(2.7)

Из (2.6) видно, что энергия диполя зависит от его ориентации во внешнем электрическом поле. График зависимости энергии диполя от угла между векторами и показан на рис. 2.3, Поскольку состоянию механического равновесия системы всегда соответствует минимум потенциальной энергии, то из энергетических соображений также следует

Рис. 2.3

полученное условие равновесия диполя во внешнем электростатическом поле.