28.3. Поглощение света

Поглощение света носит резонансный характер, т.е. из всего спектра волн, падающих на вещество, избирательно поглощаются такие волны, частоты которых соответствуют собственным частотам колебаний электронов в атомах. При этом энергия волн превращается в энергию колебательного движения электронов.

Выделим в веществе бесконечно тонкий слой толщиной dx, на который падает свет интенсивностью I. После прохождения этого слоя интенсивность света убывает на некоторую величину – dI:

(28.16)

где k — коэффициент поглощения, зависящий от частоты световой волны и рода вещества.

Разделяя переменные в (28.17) и интегрируя, получаем

(28.17)

где I_o — начальное значение интенсивности.

Соотношение (28.17) носит название закона Бугера.

В классической электродинамике доказывается, что коэффициент поглощения k численно равен модулю мнимой части диэлектрической восприимчивости æ формула (28.11):

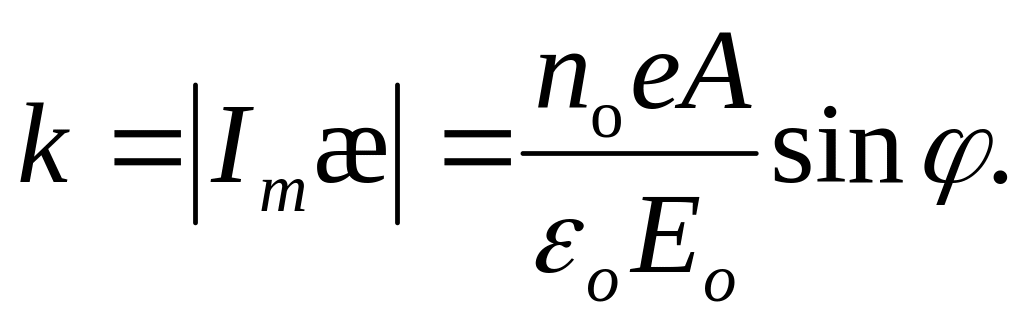
(28.18)

Используя (21.51), с помощью тригонометрического тождества

можно получить

(28.19)

Подставим (28.19) и (21.50) в (28.18). С учетом (28.9) получим выражение, описывающее зависимость коэффициента поглощения от частоты световой волны:

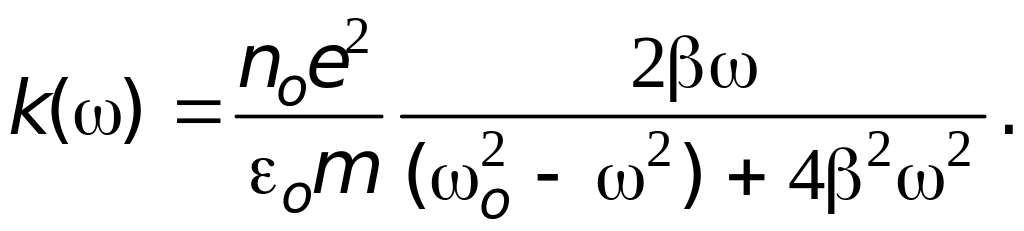
(28.20)

Из (28.20) видно, что при или  коэффици­ент поглощения k(), т.е. световые волны с очень малыми или очень большими частотами практически не поглощаются веществом. Максимум поглощения наблюдается вблизи частоты собственных колебаний электрона в атоме _o_o , (рис. 28.1, в).

Явление поглощения света (с использованием закона Бугера) применяется для количественного и качественного анализа веществ.

28.4. Рассеяние света

При прохождении света через оптически неоднородную среду его лучи отклоняются от первоначального направления — рассеиваются. Оптически неоднородной называется среда, показатель преломления которой статистически меняется от одной точки (микрообъема среды) к другой.

Наиболее просты закономерности рассеяния света для того случая, когда размеры рассеивающих областей намного меньше длины световой волны. Этот случай рассеяния экспериментально и теоретически был исследован Релеем. Сформулируем основные закономерности рассеяния света в этом случае.

1. Длина волны рассеянного света равна длине волны падающего.

2. Зависимость интенсивности рассеянного света от угла рассеяния (индикатриса рассеяния) описывается формулой

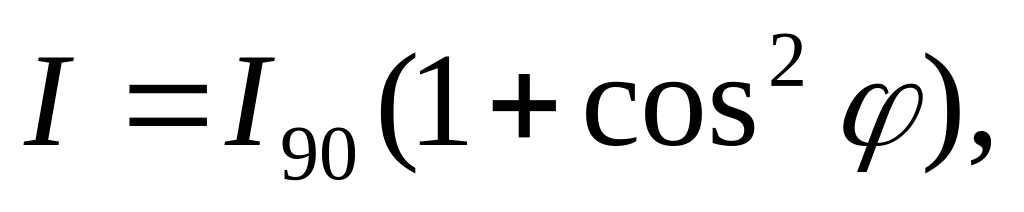
(28.21)

Рис. 28.2

где I и I₉₀—интенсивности света, рассеянного соответственно под углом φ и 90°. Графически зависимость (28.21) показана на рис. 28.2.

3. Рассеянный свет поляризован, при этом плоскость поляризации пер­пендикулярна к плоскости, в которой находятся исходный и рассеянный лучи.

4. Интенсивность рассеянного света пропорциональна четвертой степени его частоты.

Остановимся кратко на схеме рассуждений, обосновывающих это положение.

В электрическом поле световой волны электроны начинают колебать­ся по закону x = x_o sin t, где — частота световой волны. Скорость движения электронов определится выражением v = dx/dt = x_o  cos t. Движущиеся электроны — это электрический ток и сила последнего Скорость изменения тока di/dt определится, очевидно, выражением dI/dt ~ -ex₀ ² sint (т.е. пропорциональна квадрату частоты световой волны).

По первому уравнению Максвелла переменный ток создает в окружаю­щем пространстве вихревое электрическое поле, напряженность которого E пропорциональна скорости изменения магнитного потока, т.е. скорости изменения силы тока: E ~ dI/dt ~ ². Поскольку интенсивность света определяется квадратом напряженности светового вектора E, то соответственно I ~ ⁴. Поэтому при прохождении белого света через оптически неоднородную среду больше рассеиваются коротковолновые лучи (синие и голубые) и меньше рассеиваются оранжевые и красные. Голубой цвет неба и красный цвет Солнца на восходе и на закате объясняются этой закономерностью.

1 Антипараллельное расположение векторов и соответствует неустойчивому равновесию и поэтому не реализуется.

2Точнее, потоки электронов в прямом и обратном направлениях сравняются.

3 "Магнитные заряды", использовавшиеся ранее в §  17.1, представляют собой фиктивные величины и введены лишь для удобства описания.