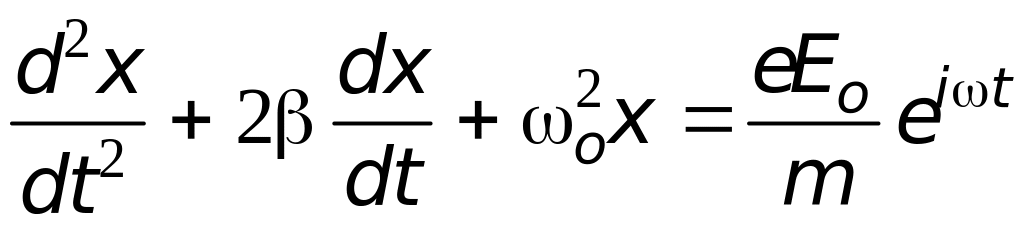- •1. Электростатическое поле в вакууме
- •1.1 Дискретность электрического заряда. Закон сохранения электрического заряда
- •1.2 Закон Кулона. Напряженность электрического поля
- •1.3. Расчёт напряжённости поля точечного заряда и электрического диполя
- •1.3.1. Напряженность поля точечного заряда
- •1.3.2. Напряженность поля электрического диполя
- •А. Напряженность поля в точке, находящейся на продолжении оси диполя
- •1.4. Силовые линии. Поток вектора напряженности. Теорема Остроградского-Гаусса
- •1.5. Применение теоремы Остроградского-Гаусса для расчета полей
- •1.5.1. Поле бесконечной равномерно заряженной плоскости
- •11.5.2. Поле двух бесконечных равномерно заряженных плоскостей
- •11.5.3. Напряженность поля бесконечной равномерно заряженной нити с линейной плотностью заряда
- •11.6. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора
- •11.7. Связь между напряженностью поля и потенциалом
- •2. Электростатическое поле в диэлектрике
- •2.1. Поляризация диэлектриков
- •2.2. Полярные и неполярные молекулы
- •2.2.1. Неполярная молекула во внешнем электростатическом поле
- •2.2.2. Полярная молекула во внешнем электростатическом поле
- •2.3. Классификация диэлектриков
- •2.4. Поляризованность. Вектор электрического смещения
- •2.4.1 Поляризованность
- •2.4.2. Связь между поляризованностью и поверхностной плотностью связанных зарядов
- •12.4.3. Связь между поляризованностью и напряжённостью поля
- •12.4.4. Вектор электрического смещения
- •12.4.5. Связь между векторами , и .
- •2.5. Нелинейные диэлектрики
- •2.5.1. Сегнетоэлектрики
- •2.5.2. Электреты
- •2.5.3. Пироэлектрики
- •3. Проводники в электростатическом поле
- •3.1. Условия на границе металл – вакуум
- •13.2. Напряжённость поля вблизи поверхности заряженного проводника
- •13.3. Электроёмкость уединённого тела и системы тел
- •13.3.1. Плоский конденсатор
- •13.3.2. Цилиндрический конденсатор
- •14. Энергия электростатического поля
- •14.1. Энергия системы точечных зарядов
- •14.2. Энергия заряженного проводника
- •14.3. Энергия заряженного конденсатора. Плотность энергии электростатического поля
- •15. Постоянный электрический ток
- •15.1. Сила и плотность тока
- •15.2. Условия существования тока. Сторонние силы. Эдс
- •15.3. Закон Ома
- •15.3.1. Закон Ома для неоднородного участка цепи
- •15.3.2. Закон Ома для полной цепи
- •15.3.3. Закон Ома для однородного участка цепи
- •15.3.4. Закон Ома в дифференциальной форме
- •15.4. Закон Джоуля-Ленца
- •15.4.1. Закон Джоуля-Ленца в интегральной форме
- •15.4.2. Закон Джоуля-Ленца в дифференциальной форме
- •15.5. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории
- •15.6. Правила Кирхгофа
- •16. Контактные и термоэлектрические явления
- •16.1. Работа выхода
- •16.2. Контактная разность потенциалов
- •16.3. Эффект Зеебека
- •16.4. Эффект Пельтье
- •17. Магнитное взаимодействие
- •17.1. Магнитное взаимодействие движущихся электрических зарядов
- •17.2. Сопоставление электрического и магнитного взаимодействий
- •17.4. Магнитное поля прямолинейного проводника с током
- •17.5. Магнитное поле кругового тока
- •17.6. Циркуляция вектора
- •17.17. Магнитное поле тороида, соленоида
- •17.8. Сила Лоренца
- •17.9. Эффект Холла
- •17.10. Сила Ампера
- •17.11. Поток вектора магнитной индукции
- •17.12. Магнитная цепь
- •17.13. Работа по перемещению проводника с током в магнитном поле
- •18.1. Эдс индукции. Правило Ленца
- •18.2. Фарадеевская трактовка явления электромагнитной индукции
- •18.3. Максвелловская трактовка явления электромагнитной индукции
- •18.4. Явления самоиндукции и взаимной индукции
- •18.5. Индуктивность тороида
- •18.6. Плотность энергии магнитного поля
- •18.7. Экстратоки замыкания и размыкания
- •18.8 Токи Фуко. Скин-эффект
- •20. Теория Максвелла
- •20.1. Ток смещения
- •20.2. Полная система уравнений Максвелла
- •19. Магнитные свойства веществ
- •19.1. Гипотеза Ампера
- •19.2. Магнитные моменты атомов
- •19.3. Вектор намагниченности
- •19.4. Слабо магнитные вещества
- •19.5. Сильномагнитные вещества
- •19.5.1. Ферромагнетики
- •19.5.2. Ферримагнетики
- •19.5.3. Антиферромагнетики
- •19.5.4. Магнитные материалы
- •21.14. Вынужденные электромагнитные колебания
- •21.14.1. Омическое сопротивление в цепи переменного тока
- •21.14.2. Индуктивность в цепи переменного тока
- •21.14.3. Емкость в цепи переменного тока
- •24.1. Уравнение плоской электромагнитной волны
- •24.2. Вектор Умова – Пойнтинга
- •24.3. Особенности распространения электромагнитных волн
- •24.4. Световые волны
- •Законы преломления
- •25.1. Когерентные источники в оптике
- •25.2. Расчет интерференционной картины от двух когерентных источников
- •25.3. Интерференция в тонких пленках
- •25.4. Стоячие волны
- •25.5. Интерферометры
- •26.1. Принцип Гюйгенса-Френеля. Расчет дифракционной картины методом зон Френеля
- •26.2. Дифракция сферических волн (дифракция Френеля)
- •26.3. Дифракция плоских волн (Дифракция Фраунгофера)
- •26.4. Дифракционная решетка
- •27.1. Общие представления о поляризации световых волн
- •27.2. Поляризация света при отражении и преломлении
- •27.3. Двойное лучепреломление
- •27.4. Поляризационные приборы
- •27.5. Закон Малюса
- •27.6. Интерференция поляризованных лучей
- •27.7. Искусственная оптическая анизотропия
- •27.8. Вращение плоскости поляризации (оптическая активность)
- •27.9. Оптические и электрооптические свойства жидких кристаллов
- •28.1. Фазовая и групповая скорости света
- •28.2. Элементарная классическая теория дисперсии
- •28.3. Поглощение света
- •28.4. Рассеяние света
28.1. Фазовая и групповая скорости света
Рассмотрим
плоскую монохроматическую волну![]() где k = 2/
— волновое число.
где k = 2/
— волновое число.
Зафиксируем некоторое значение фазы волны:
-
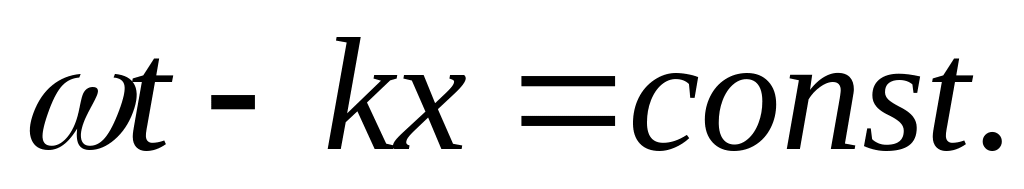
(28.1)
Скорость,
с которой перемещается в пространстве
данное значение фазы, называется фазовой
скоростью. Поскольку
![]() ,
то из выражения (28.1) следует, что
,
то из выражения (28.1) следует, что
![]()
т.е. фазовая скорость
-
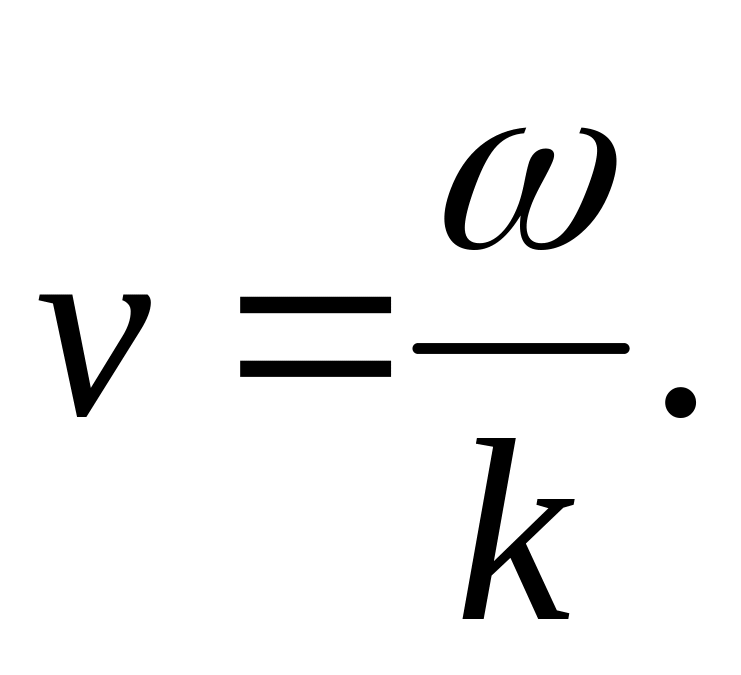
(28.2)
В реальных условиях под монохроматической волной понимается совокупность волн с частотами, заключенными в более или менее узком интервале шириной . Суперпозиция таких волн, мало отличающихся друг от друга по частоте, называется группой волн. В результате наложения волн с близкими частотами возникают биения (см. § 21.8). Точка, в которой амплитуда (а значит, и интенсивность) группы волн имеет максимум, называется центром группы волн. Центр группы волн перемещается со скоростью, которая называется — групповой.
Рассмотрим для простоты группу волн, состоящую из двух монохроматических волн с близкими частотами и :
Результирующая волна E=E1+E2 описывается уравнением
-
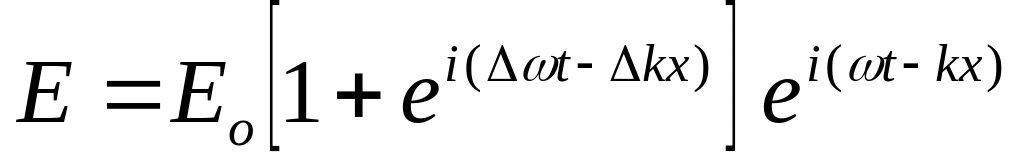 .
.
Первый множитель, стоящий в квадратных скобках, изменяется гораздо медленнее, чем второй, поэтому его можно рассматривать как амплитуду. Максимальное значение амплитуды достигается, если
Отсюда для групповой скорости получаем
или
-
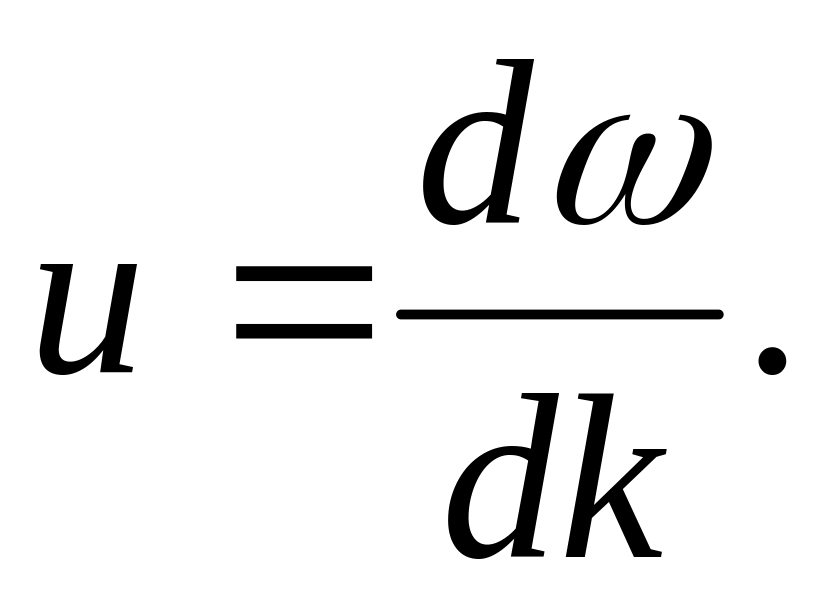
(28.3)
Найдем связь между групповой и фазовой скоростью. Так как =2, то
-
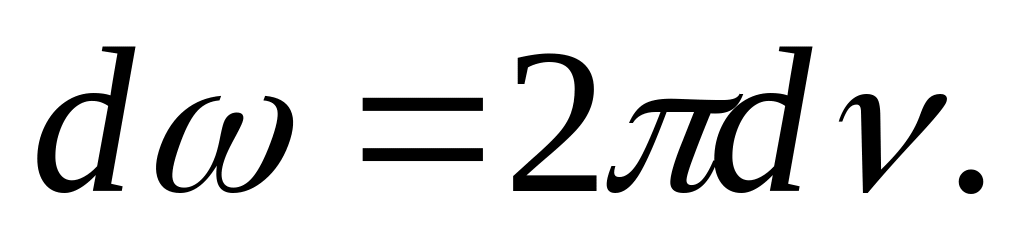
(28.4)
Далее
имеем
![]() ,
а так как
,
а так как
![]() ,
где n
— показатель преломления, то
,
где n
— показатель преломления, то
откуда
-
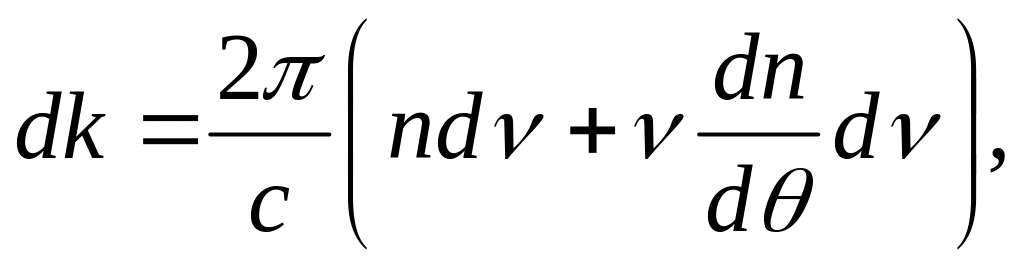
(28.5)
Подставляя (28.4) и (28.5) в (28.3), окончательно получаем:
-
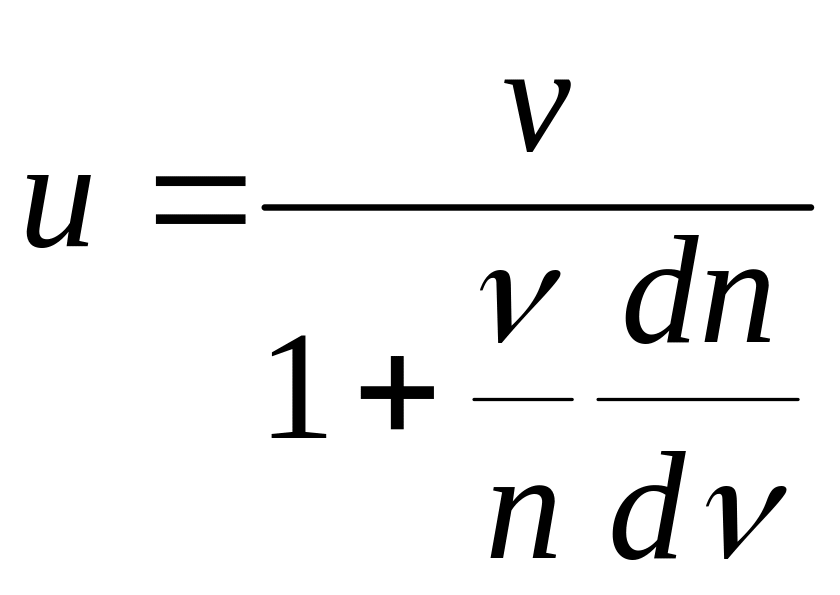
(28.6)
Из (28.6) видно, что групповая и фазовая скорости совпадают лишь в том случае, когда dn/d, т.е. показатель преломления n не зависит от частоты световой волны. В общем случае uv, поскольку n=n().
Круг явлений, в которых наблюдается зависимость показателя преломления n от частоты , называется дисперсией.
28.2. Элементарная классическая теория дисперсии
Используя
выражение (24.13), устанавливаем связь
между показателем преломления среды
![]() и диэлектрической
проницаемостью:
и диэлектрической
проницаемостью:
![]()
Поскольку æ (см. формулу (12.16)), где æ — диэлектрическая восприимчивость вещества, то
-
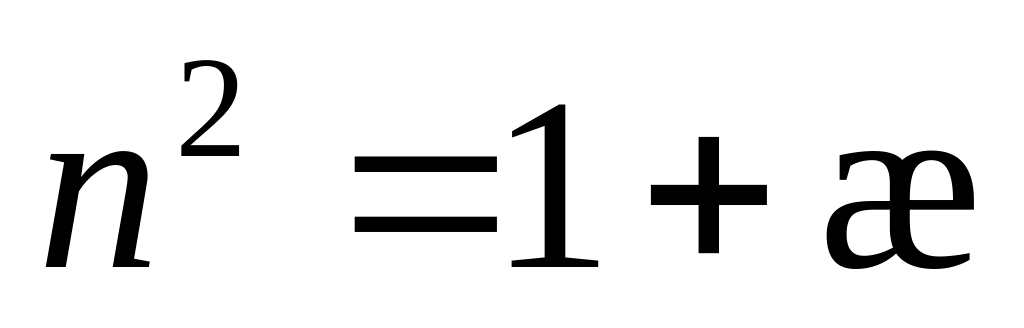
(28.7)
Таким образом, для нахождения функции n=n().необходимо найти зависимость æ от частоты
Так как световые волны обладают очень высокой частотой ( 1015Гц), то их действие на атомы вещества сводится к смещению электронов в электрическом поле световой волны и появлению деформационной поляризации.
Рассмотрим простейший случай, когда атом имеет лишь один электрон. Под действием световой волны
-
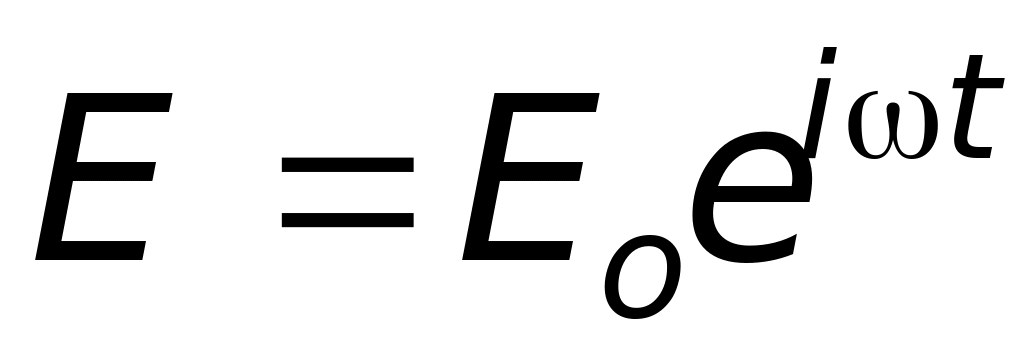
(28.8)
электрон совершает вынужденные колебания, уравнение которых (см. § 21.12):
где амплитудное значение силы, действующей на электрон се стороны электрической составляющей световой волны,
-
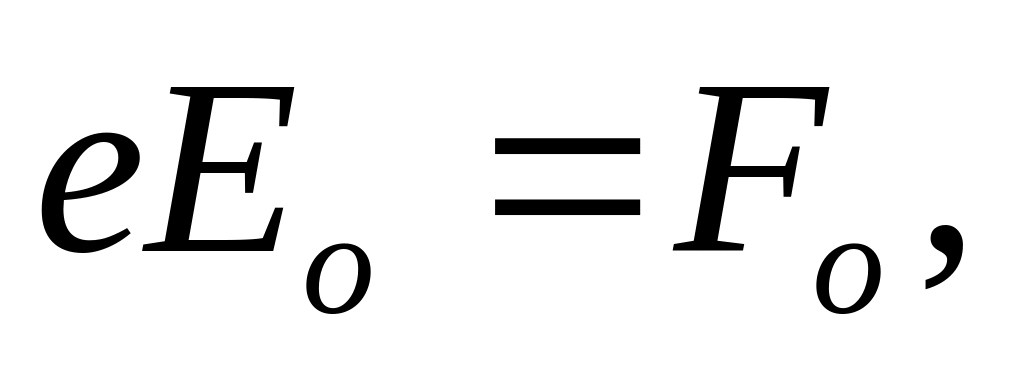
(28.9)
m —масса электрона.
Электрон смещается от положения равновесия на величину x в результате чего атом приобретает наведенный дипольный момент pe=ex. Пусть no — число атомов в единице объема вещества. Тогда поляризованность
-
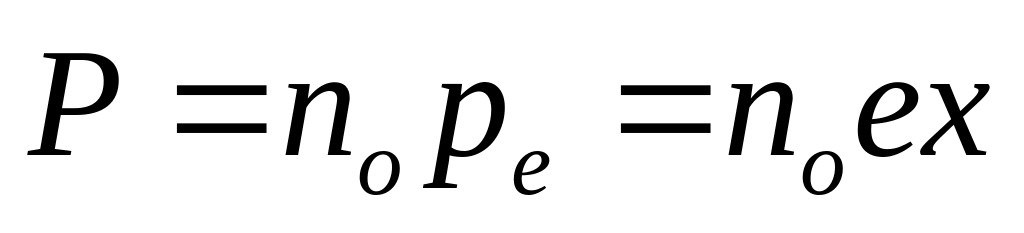
(28.10)
Однако поляризованность связана с напряженностью электрического поля соотношением (12.10). Сравнивая (28.10) и (12.10), находим диэлектрическую восприимчивость
Подставим в это выражение величину смещения x из (21.48) и значение E из (28.8). После сокращения на eit получим
-
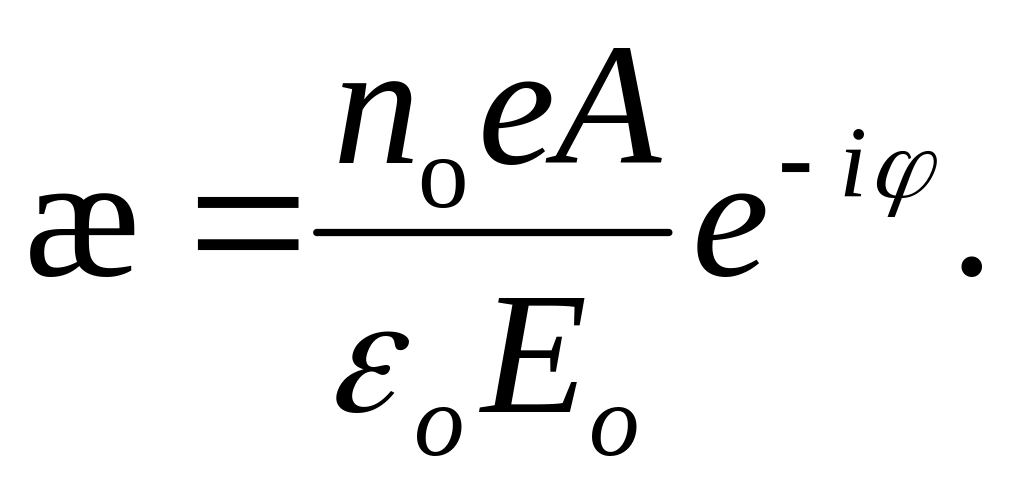
(28.11)
где A— амплитуда; — начальная фаза вынужденных колебаний электрона.
Используя формулу Эйлера (cм. Математическую справку), найдем действительную часть выражения (28.11):
Таким образом,
-
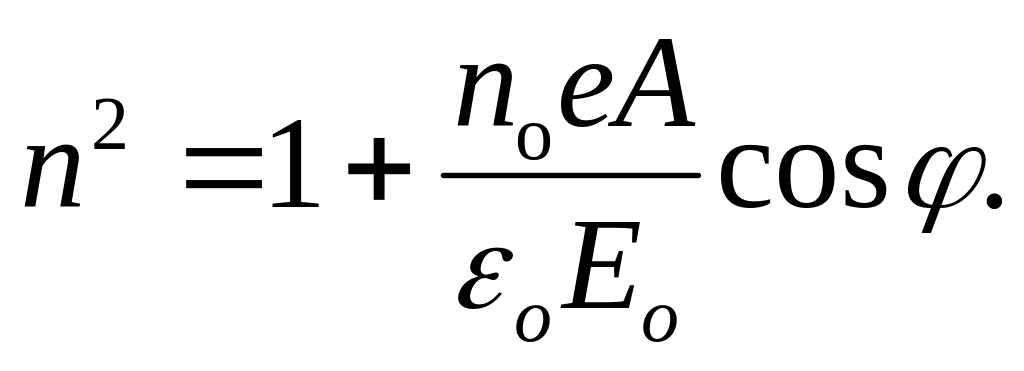
(28.12)
Воспользовавшись известным тригонометрическим тождеством
и учтя (21.51), получим
-
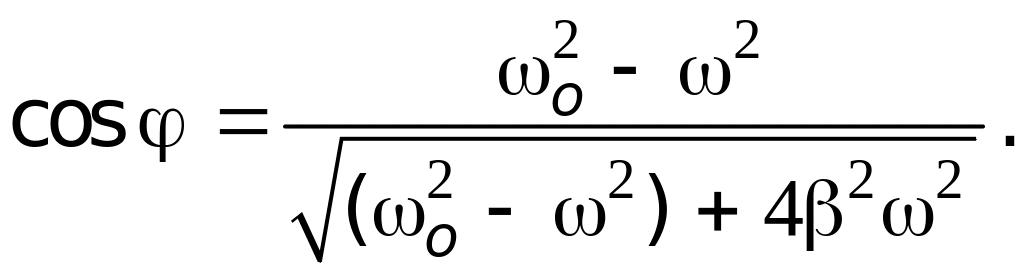
(28.13)
Подставляя (28.13) и (21.50) в (28.12) и учитывая (28.9), получаем
-
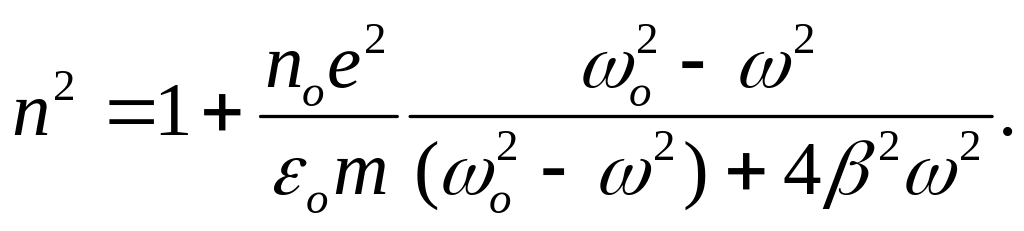
(28.14)
Если затухание отсутствует (= 0), то
-
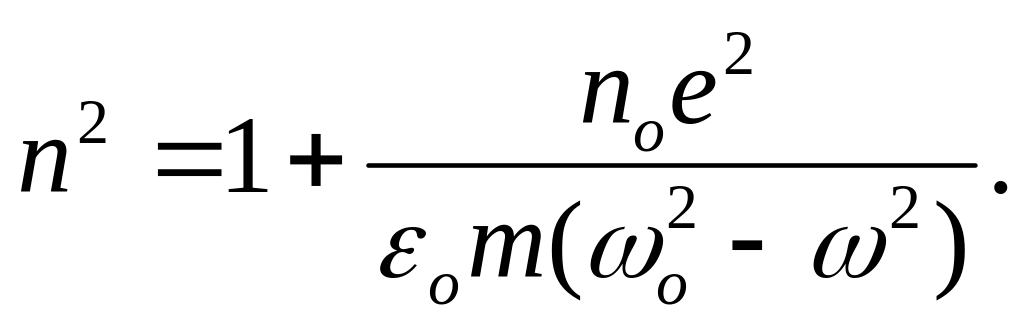
(28.15)
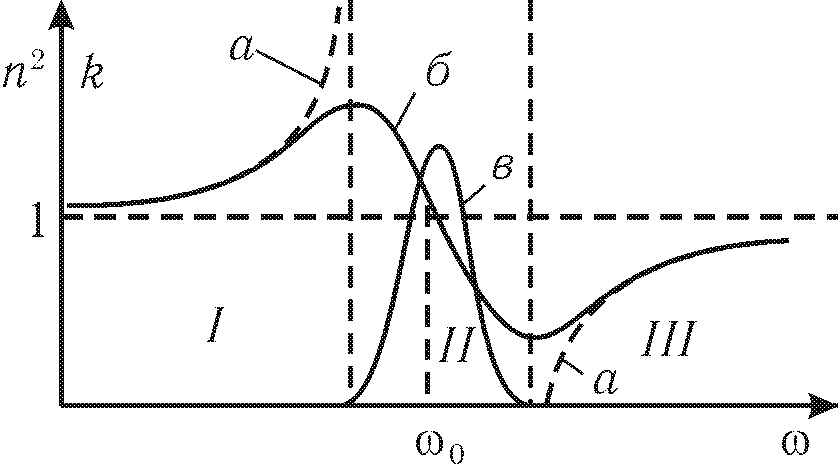
Из выражения (28.15) видно, что в области частот o при o n2, а в области частот o при o n2 – (рис.28.1,а).
Рис. 28.1