27.8. Вращение плоскости поляризации (оптическая активность)

Разместим между скрещенными поляризатором и анализатором кристалл кварца так, чтобы направление ГОО было параллельно световому лучу (рис. 27.12). При этом двойное лучепреломление не возникает, однако плоскость поляризации луча, прошедшего через кристалл, повернется на некоторый угол. В результате поле зрения полярископа просветляется и для его затемнения необходимо повернуть анализатор в противоположном направлений на угол, равный углу поворота плоскости поляризации. Было установлено, что такое явление наблюдается не только для кристаллических тел, но и для некоторых жидкостей и растворов, откуда сле­дует, что механизм, обеспечивающий вращение плоскости поляризации, связан с особенностей молекулярного строения.

Рис. 27.12

Вещества обладающие свойством вращать плоскость поляризации, называют оптически активными. Большинство из них имеет две модифика­ции — левовращающие и прав о вращающие. У правовращающей модификации поворот плоскости поляризации происходит по часовой стрелке (для наблюдателя, смотрящего навстречу лучу), у левовращающей — против ча­совой стрелки. Молекулы или кристаллы одной модификации являются зер­кальным отражением молекул или кристаллов другой модификации. Инте­ресно отметить, что при обычном химическом синтезе оптически активных органических веществ всегда одновременно образуются и право- и левовращающие модификации (изомеры) в равных количествах, в то время как продукты жизнедеятельности представляют собой только левовращающие изомеры.

Угол поворота плоскости поляризации определяется формулой

а для растворов

(27.6)

где k₁ и k₂ — коэффициенты, зависящие от рода вещества; l — длина пути в оптически активном веществе; С — концентрация оптиче­ски активного вещества в растворе.

Формула (27.6) лежит в основе определения концентрации растворов оптически активных веществ и, в частности, сахара.

В 1846 г. Фарадей обнаружил, что некоторые оптически неактивные вещества, помещенные в магнитное поле, становятся оптически активными, т.е. вращают плоскость поляризации (эффект Фарадея). Схема наблюдения эффекта Фарадея показана на рис. 27.13. Направление светового луча должно быть параллельно вектору магнитной индукции В, а угол по­ворота плоскости поляризации определяется формулой

где V — постоянная (постоянная Верде), зависящая от рода вещества; l — длина пути световых лучей в магнитном поле.

Рис. 27.13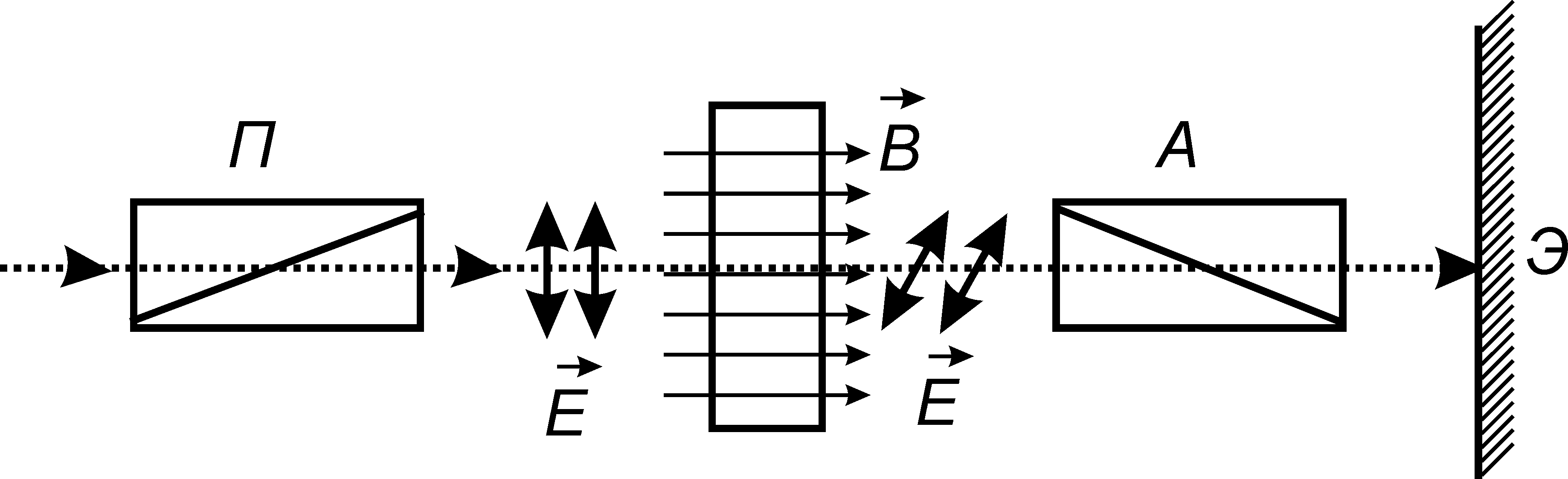

Эффект Фарадея имеет малую инерционность (10^-8 с) и наряду с эффектами Керра и Поккельса используется в оптоэлектронике для модуляции света. Преимущество эффекта Фарадея состоит в возможности использования низких напряжений, поскольку магнитная индукция B определяется значением силы тока.

27.9. Оптические и электрооптические свойства жидких кристаллов

Интересными и полезными оптическими свойствами характеризуются вещества, находящиеся в особом жидкокристаллическом состоянии, проме­жуточном между упорядоченным (кристаллическим) и неупорядоченным (жидким). Жидкие кристаллы обладают текучестью, не имеют сдвиговой упругости, характерной для твердых тел, но обладают дальней ориентационной упорядоченностью молекул, определяющей их оптические свойства.

По характеру ориентационной упорядоченности выделяют следующие типы жидких кристаллов.

1. Нематики, у которых имеется выделенное направление длинных осей молекул, но нет упорядоченности в расположении их центров масс. По оптическим свойствам нематики представляют собой одноосные кристаллы, причем направление главной оптической оси совпадает с выделенным направлением длинных осей молекул. Значение оптической анизотропии n_о–n_е для жидких кристаллов велико и обычно значительно пре­вышает такие значения для кристаллических веществ. Положением главной оптической оси жидкокристаллического образца можно управлять сравни­тельно небольшими внешними воздействиями, что открывает ряд важных практических возможностей.

2. Смектики, которые характеризуются не только существованием вы­деленного направления длинных молекулярных осей, но и упорядоченностью в расположении центров масс молекул, т.е. последние располагаются слоями. Смектики могут быть оптически двуосными, однако обладают зна­чительной вязкостью и вследствие этого значительным временем отклика на внешние воздействия, что существенно сужает возможности их приме­нения.

3. Холестерики, которые имеют особый тип упорядоченности — они характеризуются упорядоченностью слоистого типа, но направление ориен­тации длинных осей молекул закономерно изменяется от слоя к слою, т.е. их структура имеет упорядоченность спирального типа. По оптическим свойствам холестерики — это оптически активные вещества, причем кон­станта вращения плоскости поляризации для них значительно превосходят значения аналогичных констант для кристаллов и растворов.

Рассмотрим один из электрооптических эффектов для жидких кри­сталлов — эффект Фредерикса. Разместим жидкокристаллический образец между скрещенными поляризатором и анализатором так, чтобы направле­ние главной оптической оси его было параллельно лучу. В этом случае двойного лучепреломления не происходит и поле зрения будет темным — рис. 27.14,а. Если же приложить к жидкокристаллическому образцу напряжение, то все молекулы жидкого кристалла повернутся, ориентиру­ясь вдоль поля (рис. 27.14,б), главная оптическая ось жидкого крис­талла станет перпендикулярной к лучу и вследствие двойного лучепрелом­ления поле зрения просветлится. В этом и состоит эффект Фредерикса. Этот эффект носит пороговый характер, т.е. поворот главной оптической оси происходит только при определенном значении приложенного напряже­ния (U 2В).

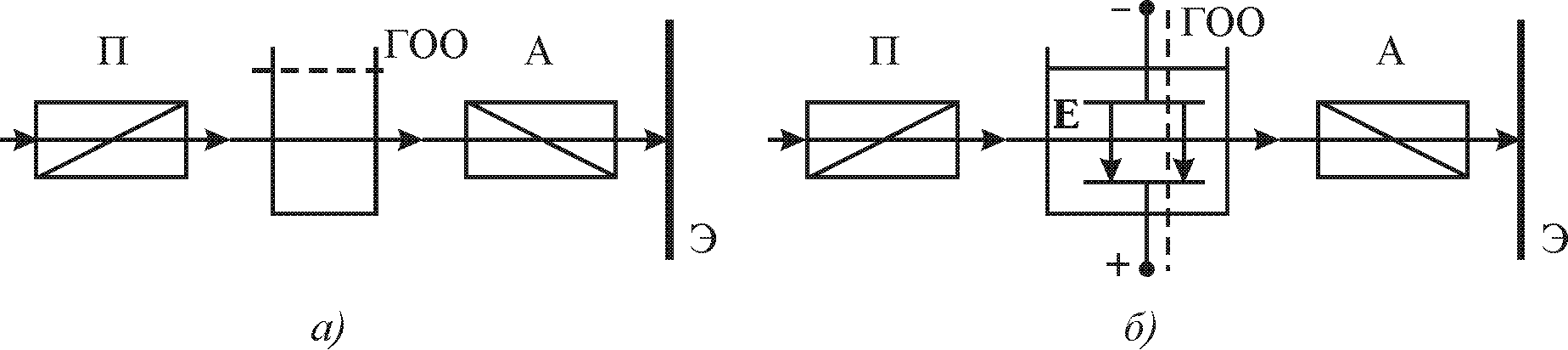
Рис. 27.14

Эффект Фредерикса применяется в разнообразных устройствах отобра­жения информации (микрокалькуляторы, транспаранты и др.), выгодно от­личаясь от других индикаторных устройств низкими управляющими напряже­ниями и малой потребляемой мощностью ( 10^-4Вт).

В индикаторных устройствах применяется также явление динамиче­ского рассеяния света, заключающееся в том, что при протекании элект­рического тока через жидкокристаллический образец в нем возникают турбулентные течения, приводящие к оптической неоднородности и значи­тельному рассеянию света. Такие индикаторные устройства требуют боль­ших напряжений (10...20 В) и больших мощностей, но позволяют созда­вать транспаранты и экраны больших размеров.

Рассмотрим теперь эффект избирательного отражения света от холе-стерических жидких кристаллов. Как было указано, для холестерина ха­рактерна слоистая спиральная структура, которая может при отражении играть роль своеобразной дифракционной решетки. Если направить на такой образец белый свет (рис. 27.15) и наблюдать в направлении зер­кального отражения, то максимум интенсивности будем видеть только для лучей тех длин волн, для которых разность хода лучей, отраженных от последовательных слоев, равна целому числу длин волн:

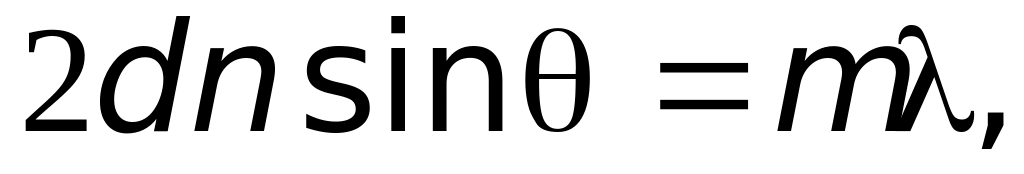
(27.7)

где n — среднее значение показателя преломления.

Рис. 27.15

Поскольку у холестериков расстояние между соседними слоями d порядка длины волны видимой части спектра, то препарат в отраженном свете окрашен. При изменении температуры изменяется толщина слоя d и вследствие этого изменяется цвет образца. Это позволяет использовать холестерики для измерения температур, причем их преимуществом является возможность исследования двумерных температурных полей, что используется в ряде медицинских и технических приложений

Лекція 36.