27.1. Общие представления о поляризации световых волн

Явление поляризации характерно только для поперечных волн, у которых направление колебаний нормально по отношению к направлению распространения волны, и таким образом может быть выделена плоскость колебаний (плоскость поляризации), проходящая через направление колебаний и вектор скорости волны.

Электромагнитные (световые) волны являются поперечными, однако у обычных источников света, состоящих из большого числа атомов, испускающих световые волны независимо друг от друга, излучение состоит из набора волн с произвольными направлениями колебаний светового вектора . Такой пучок волн со всевозможными равновероятными ориентациями вектора называют естественным светом.

С помощью определенных приемов, рассмотренных далее, из естественного света можно выделить группу световых волн, у которых плоскости колебаний светового вектора параллельны друг другу. Такая группа волн представляет собой линейно (или плоско) поляризованный свет.

В дальнейшем плоскость, в которой происходят колебания светового вектора , будем называть плоскостью поляризации (см. плоскость EOS рис. 24.1). Заметим, что раньше плоскостью поляризации называли плоскость колебаний вектора (плоскость HOS), однако такое определение оказалось неудачным и его заменили на приведенное. При рассмотрении явления поляризации достаточно указать направление колебаний светового вектора (или, что то же, плоскости поляризации), поэтому в дальнейшем плоскость, в которой происходят колебания вектора (плоскость HOS) рассматриваться не будет.

27.2. Поляризация света при отражении и преломлении

Рис. 27.1

Как было указано, при падении световых волн на границу раздела двух сред они частично отражаются, а частично преломляясь, проходят вглубь второй среды. Если обе среды диэлектрические, то, как показывает теория и эксперимент, оба эти луча становятся частично поляризованными, причем плоскость поляризации отраженного луча перпендикулярна к плоскости падения, а у преломленного совпадает с ней (рис. 27.1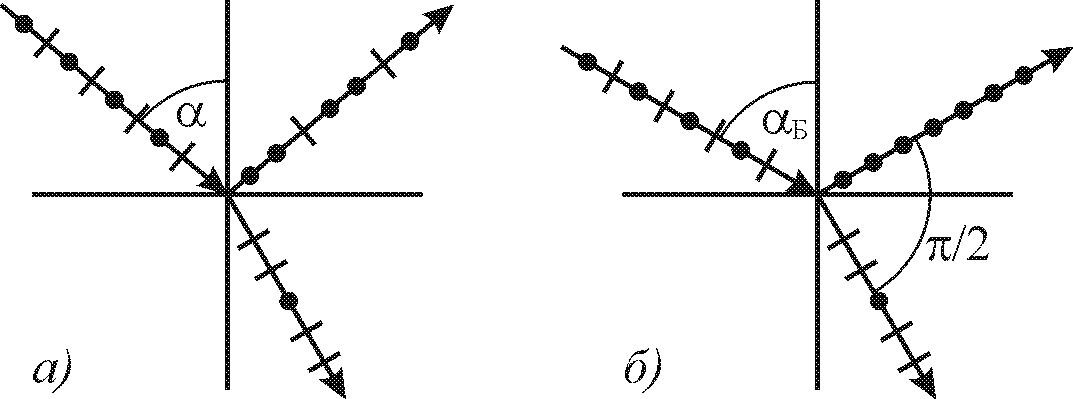, а). Если подобрать угол падения таким, чтобы угол между отраженным и преломленным лучами составлял /2, то отраженный луч оказывается полностью поляризованным (рис. 27.1, б). Такой угол падения называется углом Брюстера и его значение может быть получено из очевидных соотношений

,

а поскольку , то и, следовательно, ,

Последнее соотношение называется законом Брюстера.

Явление поляризации при отражении и преломлении применяется для поляризации света (особенно в инфракрасной области спектра).

27.3. Двойное лучепреломление

Рис. 27.2

Большинство кристаллов обладает различными оптическими свойствами в разных направлениях. Такие кристаллы называют оптически анизотропными. Для них наблюдается явление двойного лучепреломления, состоящее в том, что вместо одного преломленного луча в кристалле возникают и распространяются два преломленных луча, один из которых называется обыкновенным (о), а другой — необыкновенным (е) (рис. 27.2).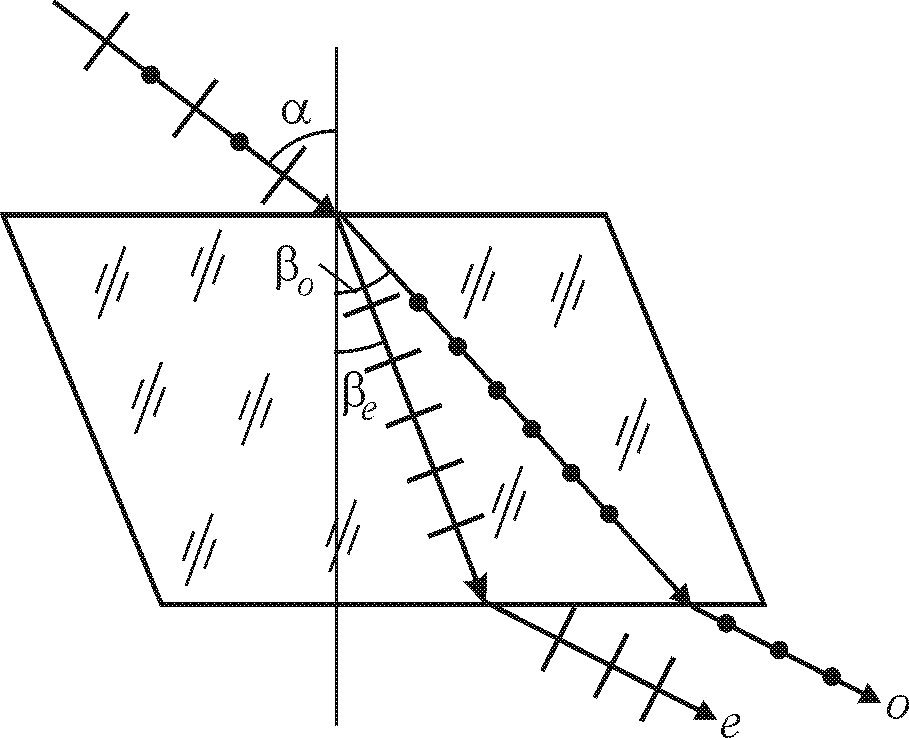

Отметим некоторые свойства обыкновенного и необыкновенного лучей.

1. Обыкновенный луч подчиняется обычным законам преломления, т.е. он лежит в плоскости падения, а отношение синуса угла падения к синусу угла преломления не зависит от угла падения. Необыкновенный луч не подчиняется законам преломления — он, как правило, выходит из плоскости падения и его показатель преломления не постоянен, а зависит от угла падения

.

2. В кристаллах существует направление, при распространении светового луча вдоль которого отсутствует двойное лучепреломление. Это направление называется главной оптической осью кристалла. В направлении оптической оси n_o=n_e, а в направлении, перпендикулярном к оптической оси, , т.е. угловое расхождение обыкновенного и необыкновенного луча максимально.

3. Кристаллы, обладающие двойным лучепреломлением подразделяются на одноосные и двухосные. У одноосных кристаллов (исландский шпат, кварц, турмалин) один из лучей обыкновенный, а другой необыкновенный. У двухосных кристаллов (слюда, гипс) оба луча необыкновенные. Одноосные кристаллы, в свою очередь, подразделяются на два класса: положительные и отрицательные. У положительных кристаллов n_e–n_o > 0, а для отрицательных n_e–n_o <0. Поскольку n_en_o, то скорости распространения обыкновенного и необыкновенного лучей различны.

4. Главным сечением кристалла (ГСК) называют плоскость, проходящую через падающий луч, и направление главной оптической оси в точке падения. Оба преломленных луча — обыкновенный и необыкновенный полностью поляризованы во взаимно перпендикулярных направлениях: плоскость поляризации необыкновенного луча совпадает с главным сечением кристалла, а у обыкновенного луча перпендикулярна к нему.

Для наглядного пояснения двойного лучепреломления можно использовать принцип Гюйгенса. При этом необходимо учесть, что зависимость показателя преломления от угла падения обусловлена зависимостью его скорости от направления.

Рассмотрим в качестве примера два случая двойного лучепреломления в одноосном отрицательном кристалле (рис. 27.3 и 27.4).

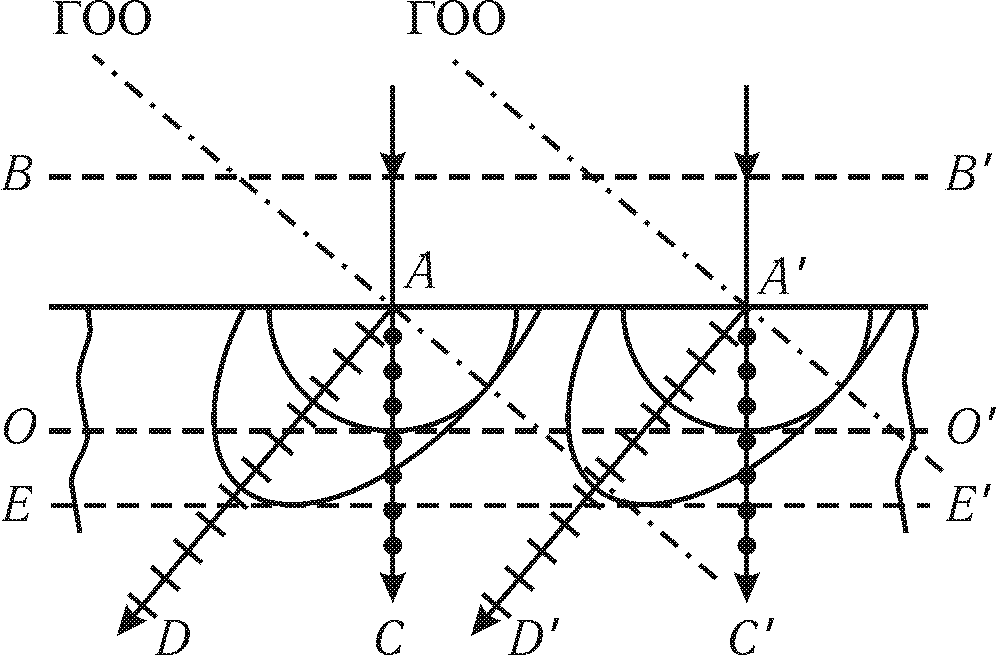
В первом случае естественные лучи падают нормально на грань кристалла, главная оптическая ось которого (ГОО) показана на рис. 27.3 штриховой линией.

Рис. 27.3	Рис. 27.4

У оптически отрицательных кристаллов n_e  n_o, а так как n = c/v, то v_e  v_o, т.е. скорость распространения необыкновенного луча больше, чем обыкновенного, причем разность v₁ – v₂ максимальна в направлении, перпендикулярном к ГОО, и равна нулю — в направлении ГОО.

Пусть в момент t=0 фронт BB^/ первичной волны касается поверхности кристалла. Для построения нового фронта выберем на поверхности кристалла две точки A и A^/. Эти точки в соответствии с принципом Гюйгенса являются источниками вторичных волн. Поскольку скорость обыкновенного луча постоянна во всех направлениях, то в этом случае вторичные волны являются сферическими. Огибающая этих волн — плоскость OO^/ согласно принципу Гюйгенса является новым фронтом.

Обыкновенный луч распространяется вдоль прямой, соединяющей точку падения с точкой касания соответствующей сферической волны с новым фронтом — линии AC и AC^/. Видно, что обыкновенный луч не преломляется.

У необыкновенного луча вторичные волны будут представлять собой эллипсоиды, причем большая ось эллипсоида перпендикулярна к ГОО, а в направлении ГОО эллипсоид и сфера касаются друг друга. Фронт необыкновенной волны — плоскость EE^/ — параллелен фронту обыкновенной волны. Однако, если теперь соединить точку падения с точкой касания соответствующей эллипсоидальной волны с фронтом EE^/ (линии AD и A^/D^/), то как видно из рис. 27.3, преломленный луч отклоняется от первоначального направления, т.е. преломляется.

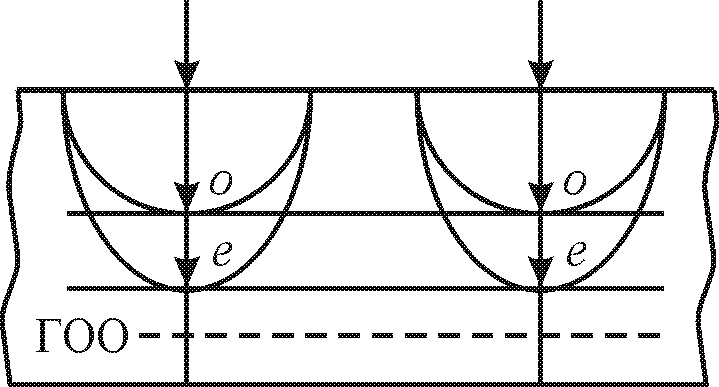
Во втором случае (см. рис. 27.4) оптическая ось параллельна внешней грани кристалла и, как видно из рис. 27.4, обыкновенный и необыкновенный лучи распространяются в кристалле в одном и том же направлении и не преломляются. Так как скорость их распространения в кристалле различна, то на выходе из кристаллической пластинки между ними возникает отличная от нуля разность фаз (см. §  27.6).