26.3. Дифракция плоских волн (Дифракция Фраунгофера)
Этот вид дифракции наблюдается в параллельных лучах. На пути этого пучка поставим экран с узкой бесконечно длинной щелью (в реальных условиях необходимо, чтобы ширина щели была значительно меньше ее длины). Лучи, прошедшие сквозь щель, собираются линзой. Дифракционная картина наблюдается на экране , помещенном в фокальной плоскости линзы (рис. 26.6).
Оптическая разность хода = NP между крайними лучами MA и NB, отклонившимися на угол , составляет
|
(26.8) |
,где a — длина щели.
Разобьем
щель MN
на зоны Френеля в виде узких полосок,
параллельных ребру щели, так чтобы
разность хода от краев этих зон отличалась
на /2.
Число таких зон будет равняться
.
Как и в предыдущем случае (§ 26.2),
результирующая амплитуда колебаний в
точке Q
определяется знакопеременной
суммой:
-
Ep = E1 – E2 + E3 – … En.
(26.10)
В данном случае все зоны Френеля равны по площади и наклонены под одним и тем же углом в направлении наблюдения, поэтому
E1 = E2 = … = En = E.
Результат суммирования в (26.10) зависит от того, четное или нечетное число зон Френеля укладывается на ширине щели (число таких зон зависит от угла наблюдения ).
Пусть на ширине щели укладывается четное число зон, т.е.
Рис. 26.6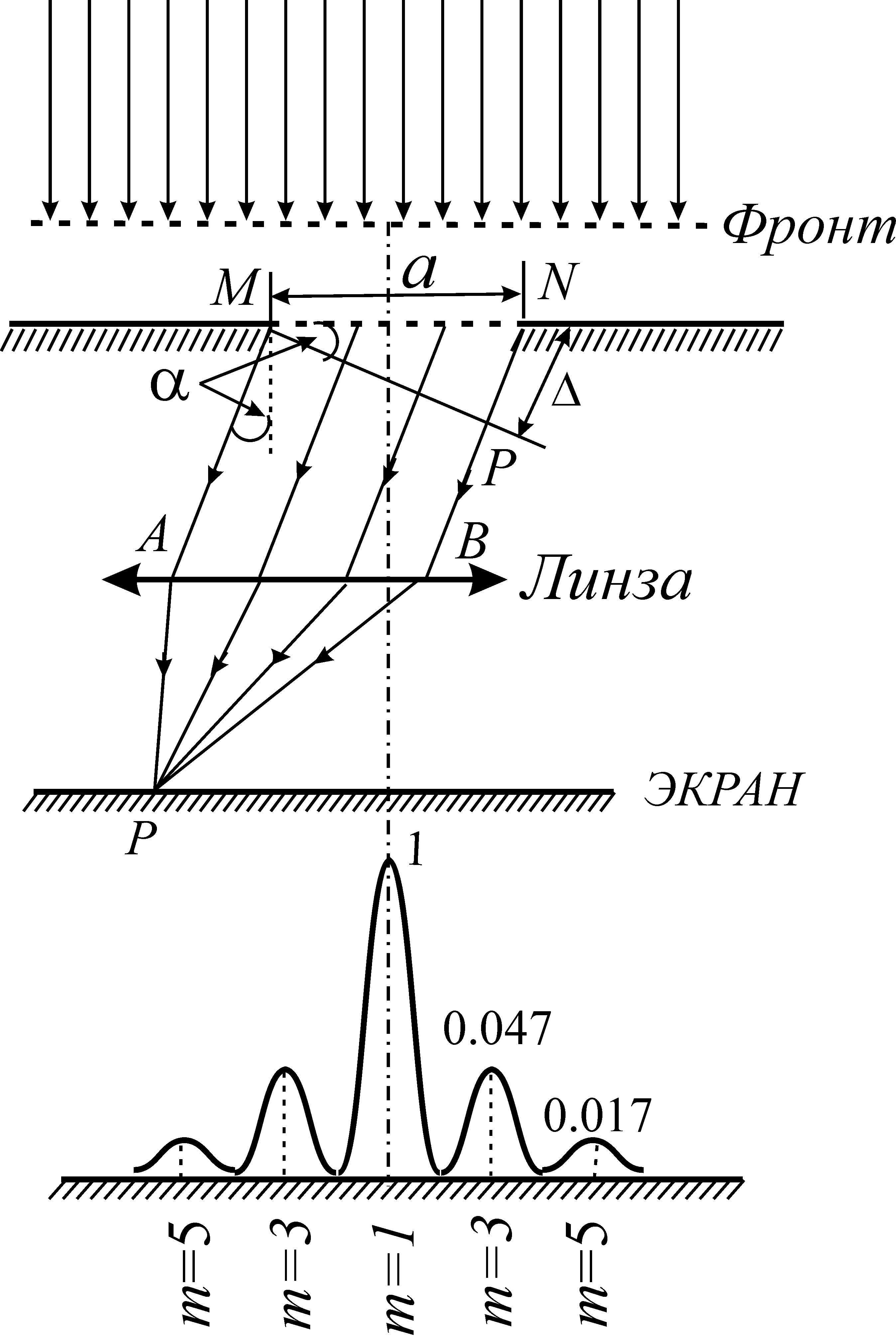
(26.11)
Легко видеть, что в этом случае сумма
Ep = E – E + E – … – E = 0.
Следовательно, если оптическая разность хода между крайними лучами равна четному числу полуволн (или, что то же, на ширине щели укладывается четное число зон Френеля), то в данном направлении наблюдается дифракционный минимум. Зоны в этом случае попарно гасят друг друга.
И наоборот, если на ширине щели укладывается нечетное число зон, т.е.
-
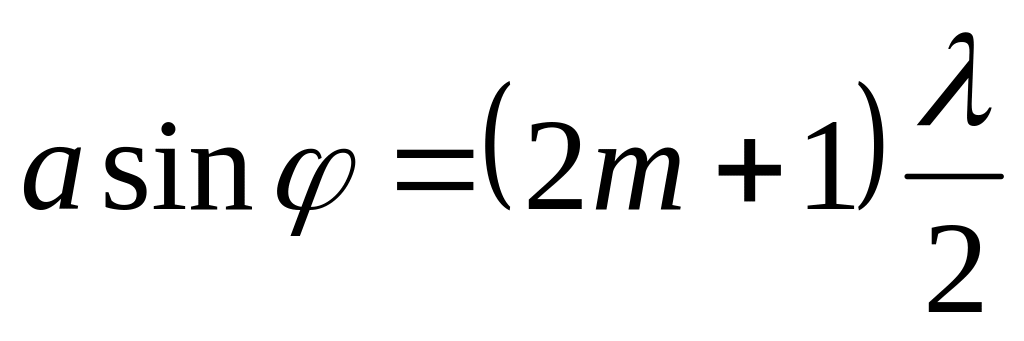,(26.12)
то
Ep = E – E + E – … + E = E.
Следовательно, если оптическая разность хода между крайними лучами равна нечетному числу полуволн (или, что то же, на ширине щели укладывается нечетное число зон Френеля), то в данном направлении наблюдается дифракционный максимум. В этом случае одна из зон остается нескомпенсированной.
Расчеты показывают, что интенсивности центрального и последующих максимумов относятся как 1:0,047:0,017:..., т.е. основная часть световой энергии сосредоточена в центральном максимуме (см. рис. 26.6).
26.4. Дифракционная решетка
Рис. 26.7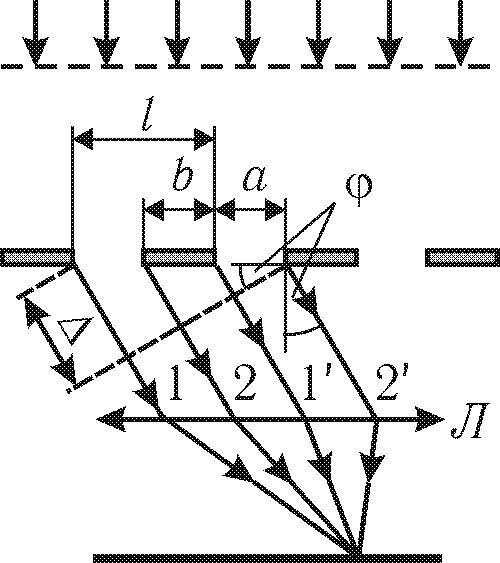
Для устранения этих недостатков применяют дифракционную решетку, т.е. совокупность параллельных щелей толщины a, разделенных одинаковыми по ширине b непрозрачными промежутками. Величина a+b=l называется периодом дифракционной решетки.
Рассмотрим вначале дифракционную решетку, состоящую из двух щелей (рис. 26.7). Лучи 1-1' и 2-2' называются соответственными. Разность хода между двумя соответственными лучами
-
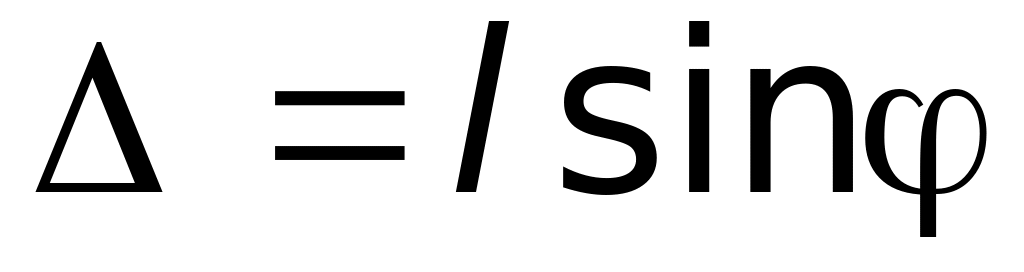,(26.12)
Очевидно, что условие минимума для одной щели сохраняется и для дифракционной решетки:
-
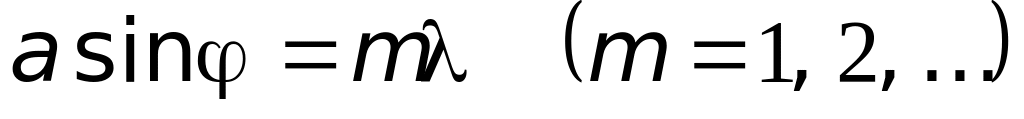.(26.13)
Применительно к дифракционной решетке условие (26.13) — это условие возникновения главных минимумов. В результате интерференции соответственных лучей, кроме того, возникают дополнительные минимумы. При этом
-
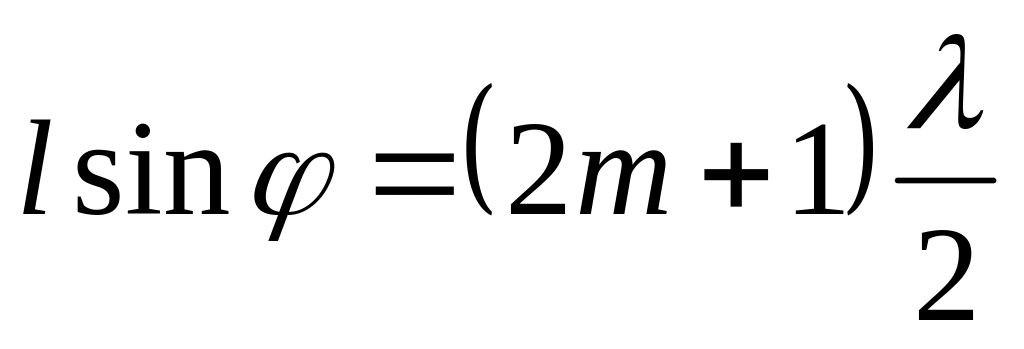,(26.14)
т.е. разность хода между соответственными лучами равна нечетному числу длин полуволн.
Между дополнительными минимумами располагаются так называемые главные максимумы. Их можно наблюдать в тех направлениях, где действие одной щели усиливает действие другой. Точнее, главные максимумы наблюдаются в том случае, когда оптическая разность хода между соответственными лучами равна четному числу длин полуволн:
,
или
-
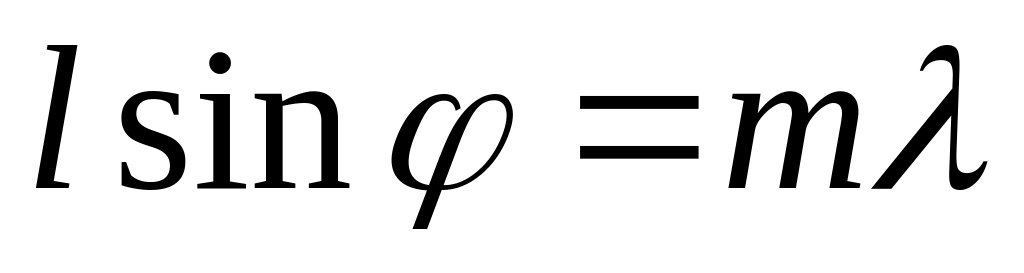.(26.15)
Таким образом, полная дифракционная картина от двух щелей описывается следующими соотношениями:
главные минимумы — a sin = m; дополнительные минимумы — ;
главные максимумы — l sin = m.
В случае, если дифракционная решетка состоит из N щелей, условия для главных минимумов и главных максимумов сохраняются, а условие для дополнительных минимумов обобщается:
-
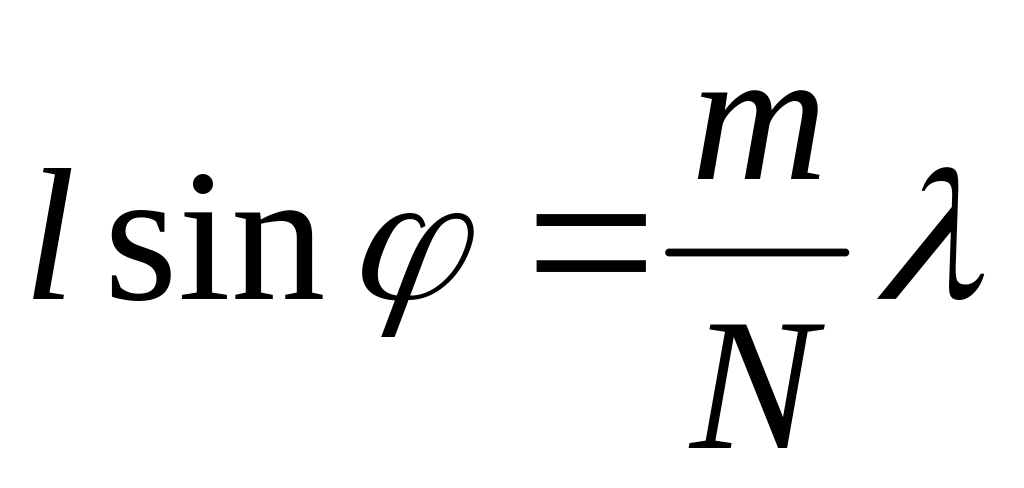.(26.16)
Рис. 26.8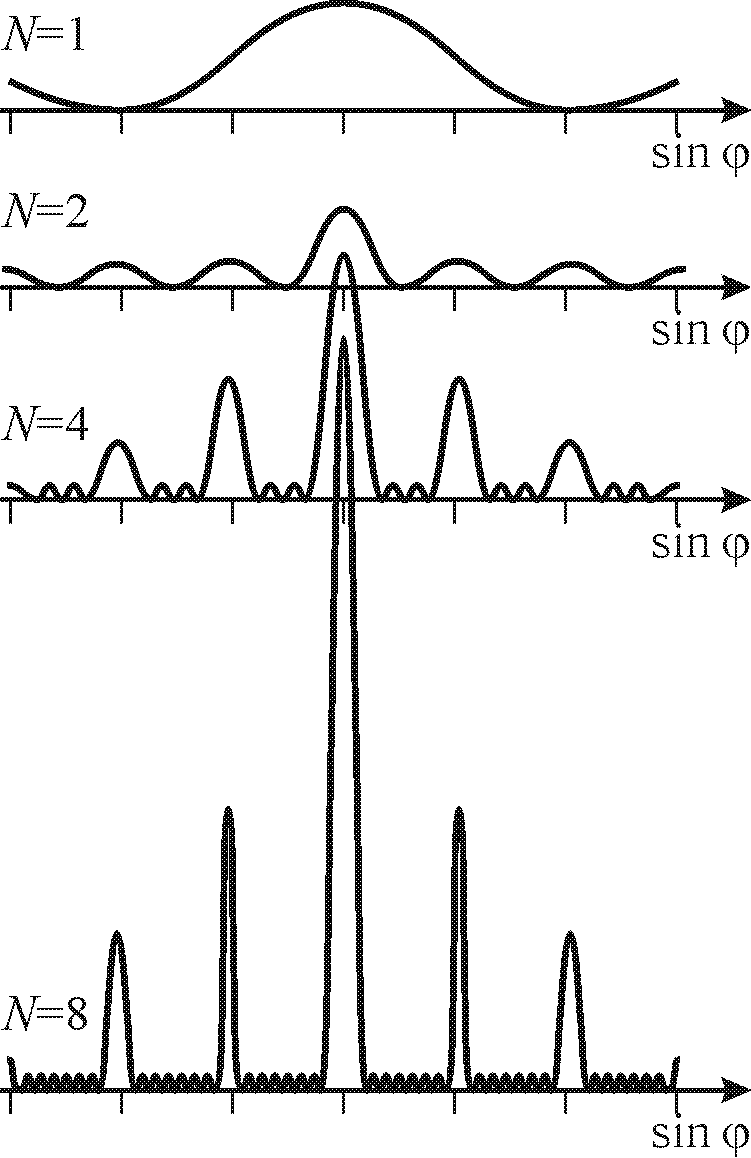
Следовательно, в случае N щелей между двумя главными максимумами располагаются N-1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон (рис. 26.8). С ростом числа щелей N возрастает интенсивность света, прошедшего через решетку. При этом число минимумов между главными максимумами возрастает и, следовательно, главные максимумы будут более интенсивными и более острыми (см. рис. 26.8, где показана дифракционная картина на одной, двух, четырех и восьми щелях).
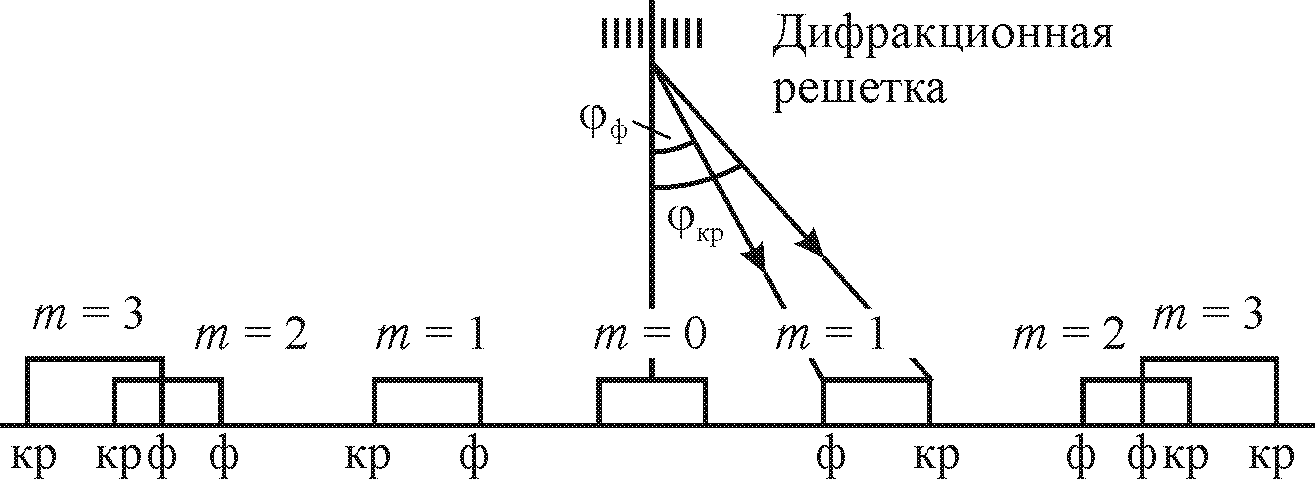
Рис. 26.9
Положение главных максимумов зависит от длины волны (см. формулу (26.15)). Поэтому, если на дифракционную решетку падает белый свет, то она разлагает его в спектр. При этом, чем больше длина волны , тем на больший угол происходит отклонение (рис. 26.9). При m=1 получаем спектр первого порядка, при m=2 — спектр второго порядка и т.д. Спектры второго и третьего порядка могут частично перекрываться. Чем больше порядок спектра, тем меньше его интенсивность. На практике обычно используют спектры первого и второго порядков.
Таким образом, дифракционная решетка является спектральным прибором и служит для определения спектрального состава света.
В заключение рассмотрим одну из важнейших характеристик дифракционной решетки — ее разрешающую способность.
Разрешающей способностью спектрального прибора называют безразмерную величину
,
где
— абсолютное значение минимальной
разности длин волн двух соседних
спектральных линий, при которой эти
линии регистрируются раздельно. Согласно
критерию Релея, раздельная регистрация
двух спектральных линий возможна, если
интенсивность провала составляет 80 %
интенсивности в максимуме (рис. 26.10, а).
Если критерий Реллея не выполняется,
то раздельное наблюдение линий невозможно
(рис. 26.10, б).
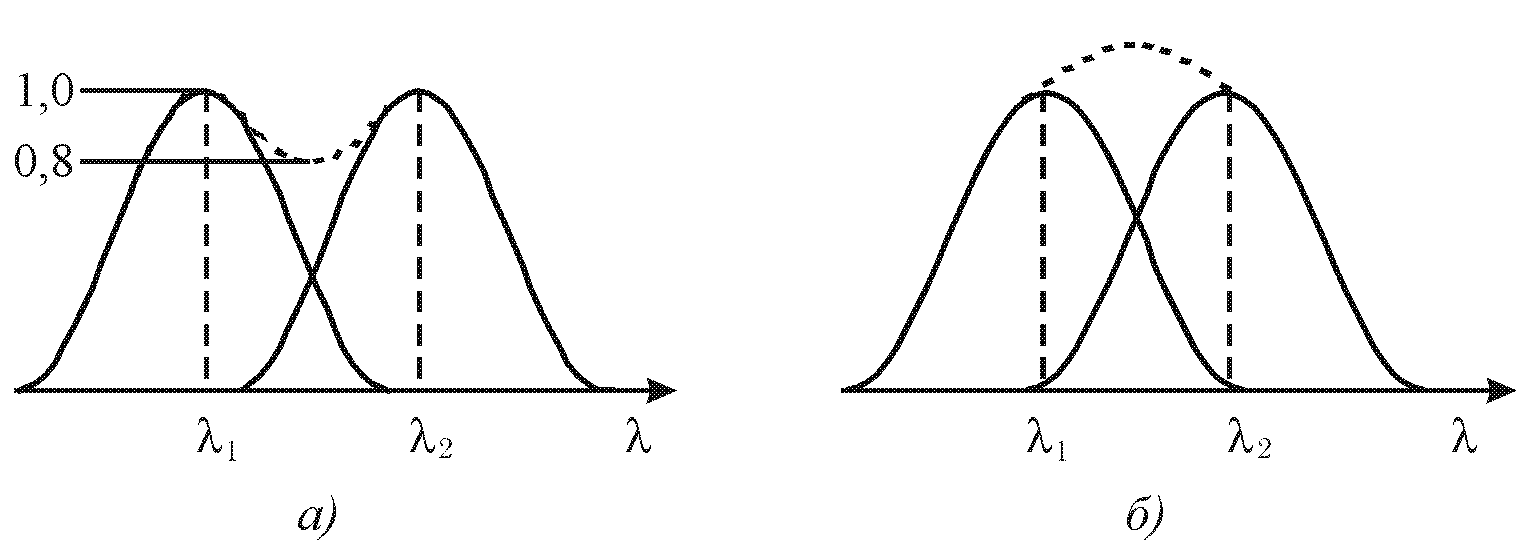
Рис. 26.10
Можно показать, что для дифракционной решетки R=mN, т.е. разрешающая способность дифракционной решетки пропорциональна порядку спектра m и числу щелей N. Для современных решеток R ~ 2·105.
Лекція 35.