25.4. Стоячие волны

Частным случаем интерференции является образование стоячих волн.

Стоячие волны возникают при интерференции двух встречных когерентных волн с одинаковой амплитудой. Такая ситуация может возникнуть при отражении волны от преграды и наложении ее на гладкую волну.

Падающая волна описывается уравнением

,

Уравнение отраженной волны

,

Разность фаз интерферирующих волн

.

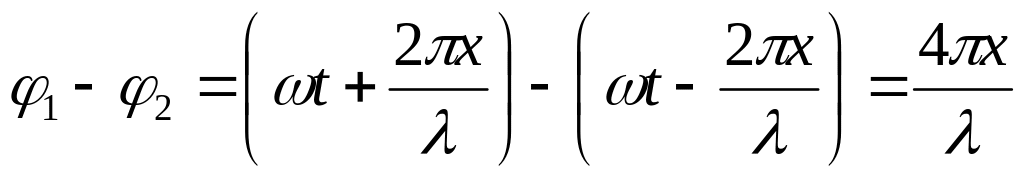(25.11)

Результирующую амплитуду колебаний при наложении волн в точке пространства с координатой x найдем по формуле (21.24), заменив в ней разность фаз по (25.11) и положив A₁ = A₂ = E₀. Имеем

;

.

Пусть x₁, x₂,..., x_k — координаты точек, для которых разность фаз

.

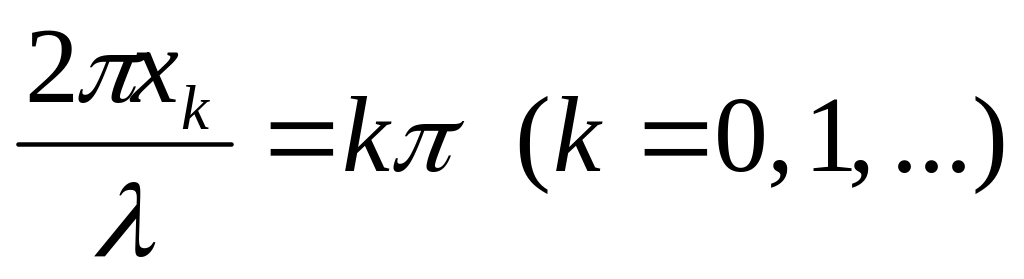(25.12)

Тогда

,

т.е. для точек удовлетворяющих условию (25.12), выполняется условие максимума — в этих точках результирующая амплитуда равна удвоенной амплитуде одной из волн. Эти точки называются пучностями. Координаты пучностей

.

Расстояние между соседними пучностями равно половине длины волны:

.

В точках x₁, x₂, ..., x_k, где

,

результирующая амплитуда

,

т.е. для этих точек выполняется условие минимума. Эти точки называются узлами. Координаты узлов:

.

Расстояние между узлами равно :

.

Рис. 25.5

Характерные особенности стоячей волны следующие: точки, лежащие по разные стороны от данного узла, колеблются в противофазе, а во всех точках, расположенных между двумя соседними узлами, колебания происходят в одной и той же фазе (синфазно) — рис. 25.5.

В стоячей волне в отличие от бегущей нет переноса энергии, а происходят локализованные в пространстве процессы превращения энергии из одного ее вида в другой (например, кинетической в потенциальную в упругой стоячей волне).

В качестве примеров образования механических стоячих волн можно привести стоячие волны, возникающие на колеблющихся струнах музыкальных инструментов. При этом на концах струны располагаются узлы, а между ними размещаются одна или несколько пучностей. Стоячие волны (сейши) иногда образуются в закрытых водоемах. Стоячие световые волны (несмотря на то, что расстояние между пучностями было менее 1 мкм) в фотографических эмульсиях; они образуются также в резонаторах оптических квантовых генераторов (лазеров) (см. §  35.3).

25.5. Интерферометры

Интерферометры — это измерительные приборы, в которых для решения определенных задач используется явление интерференции волн.

Принцип действия всех интерферометров одинаков; различаются они лишь методом получения когерентных световых волн, а также тем, какая величина непосредственно измеряется. Пучок света с помощью того или иного устройства разделяется на два когерентных пучка, которые проходят различные оптические пути и затем сводятся вместе, образуя интерференционную картину. Рассмотрим несколько типов оптических интерферометров.

Рис. 25.6

1. Интерферометр Майкельсона. Параллельный пучок света от источника S направляется на зеркало З и разделятся на два когерентных пучка 1 и 2. После отражения от зеркал З₁ и З₂ лучи проходят зеркало З параллельно друг другу, образуя интерференционную картину, которую можно наблюдать через окуляр О (рис. 25.6).

Поскольку расстояния l₁ и l₂ лучи 1 и 2 проходят дважды, то оптическая разность хода между ними  = 2(l₁–l₂). При перемещении одного из зеркал на расстояние /4 разность хода изменится на /2 и произойдет полная смена освещенности поля зрения — максимумы сменятся минимумами. Интерференционная картина восстановится, если дополнительно переместить это же зеркало в том же направлении на расстояние /4.

Поскольку регистрируются незначительные изменения интерфренционной картины, можно измерять перемещения зеркала с точностью до 0,01. Это позволяет использовать интерферометр Майкельсона в метрологических целях для установления и последующего воспроизведения эталона длины с помощью концевых мер, представляющих собой тщательно выполненные бруски из твердых сплавов.

В сочетании с микроскопом интерферометр Майкельсона позволяет по виду интерференционной картины измерять величину отступлений исследуемой поверхности от плоскости и форму микронеровностей на ней.

Рис. 25.7

2. Интерферометр Релея. Оптическая схема интерферометра Релея показана на рис. 25.7. Лучи, идущие от источника света S, с помощью диафрагмы разделяются на два когерентных пучка, проходят кюветы K₁ и K₂, а далее сводятся в одну точку и интерферируют.

Если показатели преломления веществ (газов, жидкостей), находящихся в кюветах K₁ и K₂, отличаются друг от друга, то между пучками возникает оптическая разность хода, которая составляет =n₁l–n₂l = (n₁–n₂)l и интерференционная картина изменяется. Этот интерферометр позволяет с высокой точностью (до 10^-6-10^-7) измерять различия в показателях преломления и надежно устанавливать наличие малых количеств вредных веществ в газах и жидкостях.

Рис. 25.8

3. Кольцевой интерферометр Саньяка. В современном варианте интерферометра Саньяка в качестве источника света используется лазер, генерирующий остронаправленное монохроматическое излучение. Лазерные лучи с помощью зеркал распространяются по замкнутому пути в двух взаимно противоположных направлениях (рис. 25.8). С помощью специального оптического устройства, условно показанного на рис. 25.8 в виде призмы, лазерные лучи частично выводятся из интерферометра, распространяясь при этом в одном и том же направлении и образуя устойчивую интерференционную картину. Если же интерферометр привести во вращение с некоторой угловой скоростью вокруг оси, перпендикулярной к его плоскости, то вследствие эффекта Доплера частоты встречных световых волн изменятся. В результате сложения световых колебаний с различными частотами возникнут биения, и интерференционная картина будет перемещаться со скоростью, определяемой частотой биений. При использовании фотодетектора с размерами чувствительной площадки, много меньшими расстояния между интерференционными полосами, можно измерять скорость вращения кольцевого лазера, измеряя скорость прохождения светлых полос через чувствительную площадку фотодетектора.

Направление смещения интерференционных полос определяется направлением вращения интерферометра. Используя два фотодетектора вместе с логической схемой и реверсивным счетчиком, можно установить направление вращения и посчитать разность числа импульсов, соответствующих повороту в ту или иную сторону. Такая система называется лазерным гироскопом. Разность числа импульсов зависит только от конечного угла, на который повернулся лазерный гироскоп, и не зависит от изменений скорости вращения. В частности, если гироскоп был вначале повернут на некоторый угол влево, а затем на такой же угол вправо, то реверсивный счетчик покажет нулевое число импульсов.

Указанные свойства лазерного гироскопа используются в системах корректировки курса быстро летящих объектов — ракет, самолетов и т.д. Перспективно также применение этих гироскопов на морском флоте для создания систем управления судном, однако их внедрение в морскую практику сдерживается пока недостаточной чувствительностью этих приборов при малой угловой скорости вращения.

Лекція 34.