25.2. Расчет интерференционной картины от двух когерентных источников

Выясним условия возникновения интерференционных максимумов или минимумов при интерференции волн от двух когерентных источников S₁ и S₂. В общем случае эти источники могут находиться в различных средах с показателями преломления n₁ и n₂. При этом оптические когерентные источники излучают световые волны с одинаковой частотой , но различными длинами волн:

,

где — длина световой волны в вакууме.

В точке P (рис. 25.2) накладываются две волны, уравнения которых

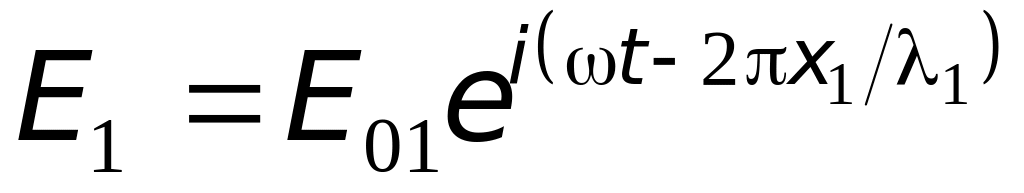,	(25.1)
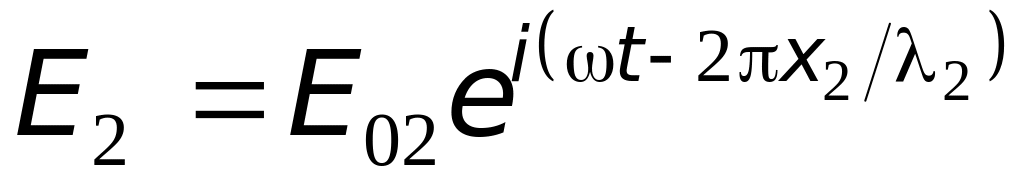,	(25.2)

где x₁ и x₂ — расстояния от источников до рассматриваемой точки P, а вектора и направлены одинаково (например, перпендикулярно к плоскости чертежа).

Рис. 25.2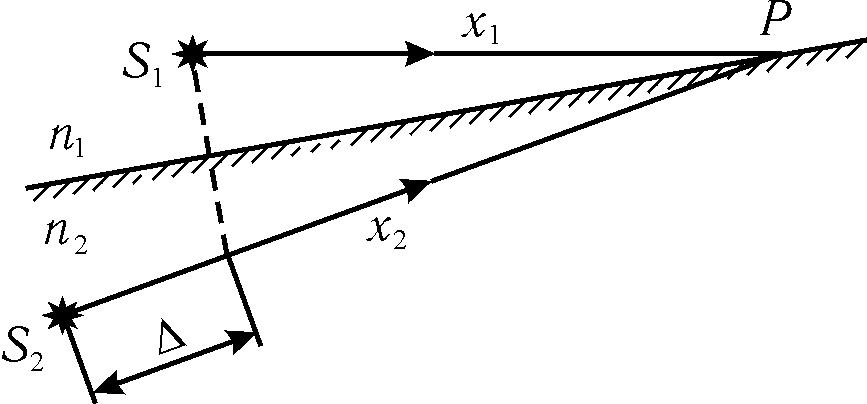

Расчет результирующей амплитуды и соответственно интенсивности световой волны в точке P можно выполнить как сложение скалярных колебаний одинаковой частоты (см. §  21.8).

Разность фаз складываемых колебаний на основании (25.1) и (25.2) составляет

Выразив длины волн _ и ₂ через длину волны в вакууме, можно записать

.

Разность  = n₂x₂ – n₁x₁ называется оптической разностью хода. Таким образом, разность фаз

.

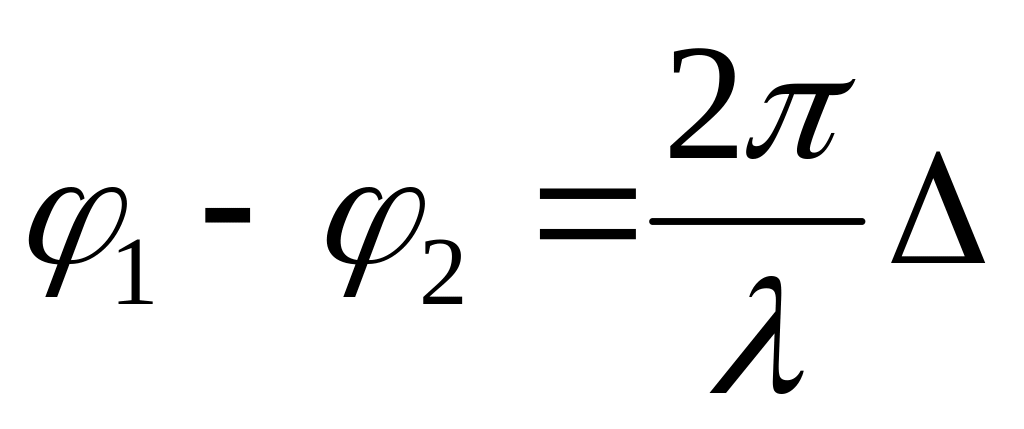(25.3)

Подставив (25.3) в (21.24), найдем значение результирующей амплитуды колебаний в точке P

,

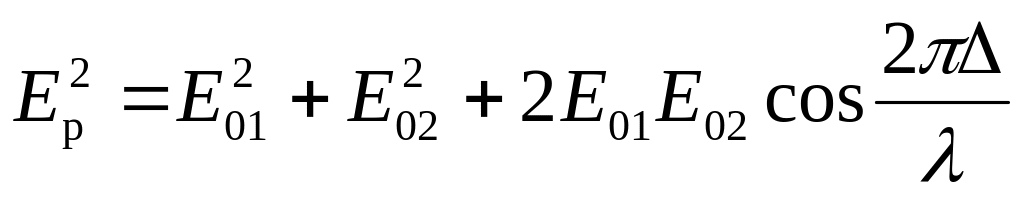(25.4)

Рассмотрим частные случаи.

1. Оптическая разность хода равна целому числу полуволн:

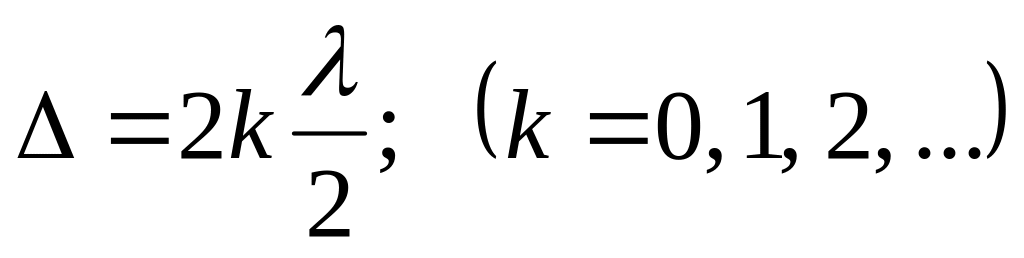
	(25.5)
;
;
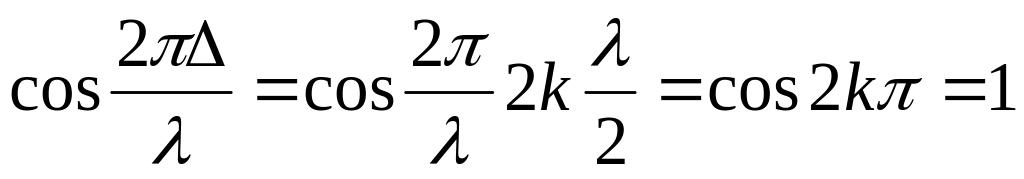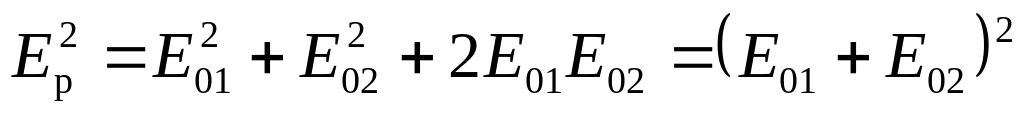.	(25.6)

Из (25.6) видно, что в этом случае результирующая амплитуда колебаний равна сумме амплитуд, т.е. происходит взаимное усиление колебаний и интенсивности. Таким образом, условие (25.5) есть условие возникновения интерференционного максимума.

2. Оптическая разность хода равна нечетному числу полуволн:

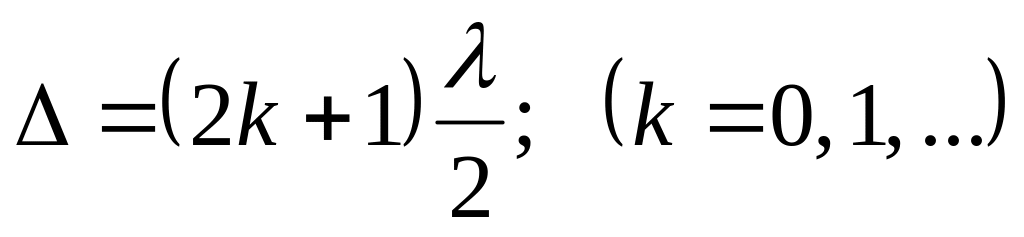
	(25.7)
;
;
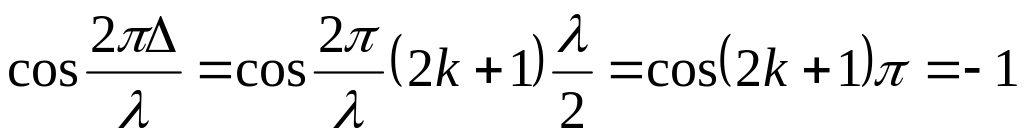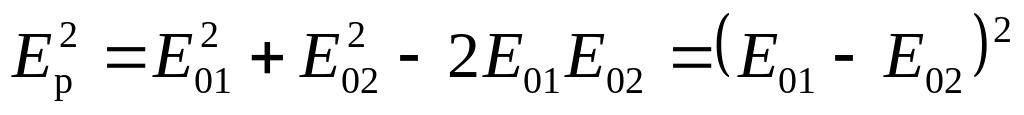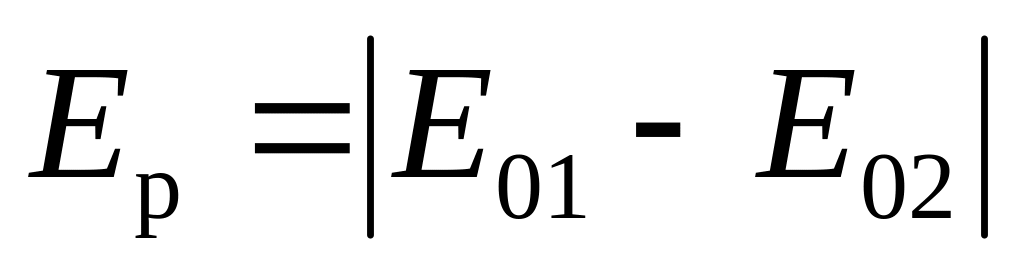.	(25.8)

Из (25.8) видно, что результирующая амплитуда колебаний равна разности амплитуд, т.е. происходит взаимное ослабление амплитуд колебаний. В случае, если E₀₁ = E₀₂, происходит полное гашение, т.е. E_p = 0. Таким образом, условие (25.7) есть условие возникновения интерференционного минимума.

25.3. Интерференция в тонких пленках

Рис. 25.3

Важным в практическом отношении случаем интерференции световых волн является интерференция света в тонких пленках.

Пусть на поверхность расположенной в воздухе тонкой прозрачной пленки толщиной h и с показателем преломления n падает световой луч (рис. 25.3). В точке A световой луч частично отражается (луч 1') и частично преломляется. Преломленный луч отражается в точке B и возвращается обратно — луч 2'. Лучи 1' и 2' когерентны, так как они образовались в результате разделения одного и того же падающего луча. Оптическая разность хода между ними

.

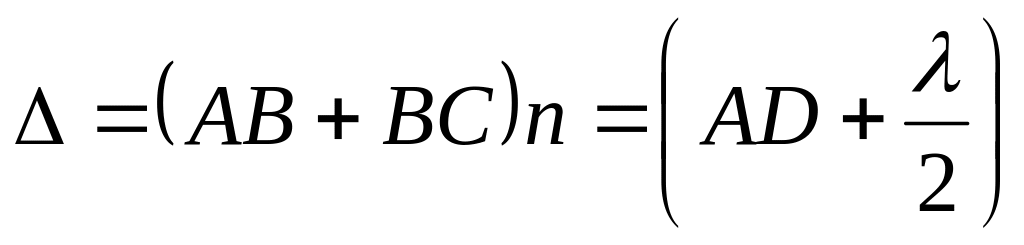(25.9)

Необходимость учета дополнительного слагаемого /2 связана с тем, что условия отражения световых лучей в точках A и B различны. В точке A отражение происходит от оптически более плотной среды; при этом фаза световой волны изменяется на , что эквивалентно разности хода /2. В точке B световая волна отражается от оптически менее плотной среды и ее фаза при этом не изменяется.

Из рис. 25.3 видно, что

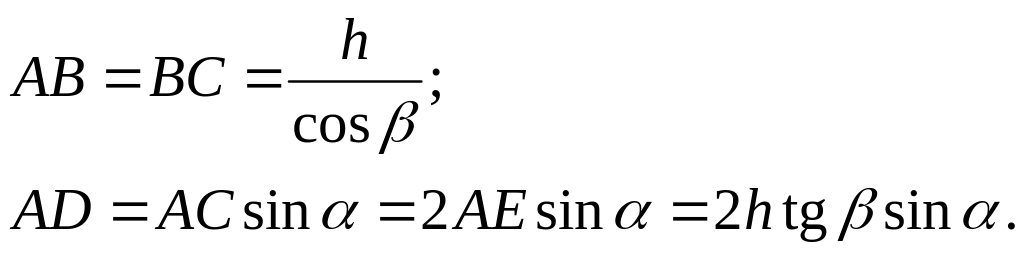
Подставив эти выражения в (25.9) и заменив с помощью закона преломления (24.16) угол преломления  на угол падения , после несложных преобразований получим

.

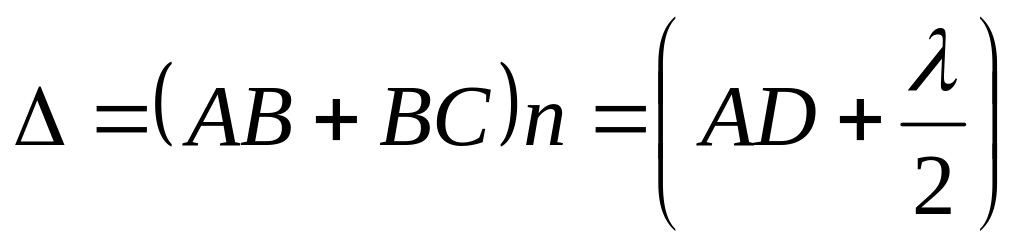(25.10)

Из (25.10) видно, что оптическая разность хода зависит от трех параметров: толщины пленки h, угла падения  и длины волны , т.е.  = f(h, , ). Для анализа результата интерференции рассмотрим частные случаи, когда одни из параметров — переменный, а остальные фиксированы.

1. Пусть h=const, =const, const, т.е. на пленку постоянной толщины под одним и тем же углом падает белый свет. Тогда, в зависимости от длины волны, будет выполняться либо условие максимума (25.5), либо условие минимума (25.7). Вследствие этого пленка в отраженном свете будет окрашенной — будут видны те цвета (изохромы), которым соответствуют длины волн, удовлетворяющие условию максимума. Дополнительные цвета будет видны в проходящем свете: этим цветам соответствуют длины волн, которые удовлетворяют условию минимума в отраженном свете и условию максимума в проходящем свете.

Рис. 25.4

2. Пусть h=const, const, =const, т.е. на пленку постоянной толщины под различными углами падает монохроматический свет. В этом случае на пленке в отраженном свете будет видны светлые и темные полосы. Эти полосы называются линиями постоянного наклона, так как каждая из них проходит по таким местам пленки, где угол падения один и тот же: светлые полосы соответствуют углам наклона, удовлетворяющим условию максимума, темные — условию минимума. Разным линиям соответствуют различные, но постоянные углы падения. Если источник точечный, то на пленке будут видны концентрические темные и светлые окружности (рис. 25.4).

3. Пусть hconst, =const, =const, т.е. на пленку переменной толщины под одним и тем же углом падает монохроматический свет. На пленке будут видны темные и светлые полосы, каждая из которых проходит по таким ее местам, где толщина одна и та же (линии равной толщины). Разным линиям соответствуют различные, но постоянные толщины. Если, например, взять проволочный каркас с мыльной пленкой и поставить его вертикально, то за счет стекания жидкости она приобретет форму клина и на ней будут видны горизонтальные светлые и темные полосы.

Явление интерференции света в тонких пленках лежит в основе просветления оптики. Современные оптические приборы (объективы фотоаппаратов, бинокли, секстанты, перископы и т.д.) содержат большое число оптических элементов (линз, призм и т.п.). Прохождение света через каждый из таких элементов сопровождается частичным отражением, что может привести к существенной (до 40 %) потере интенсивности. Для уменьшения потерь на отражение на поверхность оптических элементов наносят тонкую пленку вещества, подбирая ее толщину так, чтобы разность хода отраженных лучей удовлетворяла условию минимума. Кроме того, как показывают теоретические расчеты, для полного гашения отраженных лучей необходимо подобрать пленку с показателем преломления, равным корню квадратному из показателя преломления стекла. При выполнении этих условий отражение прекращается, что существенно увеличивает светосилу оптических приборов.