24.4. Световые волны
К световым волнам относятся электромагнитные волны, воспринимаемые нашими органами зрения. Длины световых волн расположены в пределах от 400 до 700 нм. Субъективная характеристика световых волн — их цвет определяется длиной волны: фиолетовому цвету соответствует ф = 400 нм, красному — к = 700 нм.
При
взаимодействии света с неферромагнитными
средами основную роль играет электрическая
составляющая электромагнитной волны,
поэтому в дальнейшем мы будем
абстрагироваться от значительно более
слабого взаимодействия с магнитной
составляющей. Вектор напряженности
электрического поля световой волны
в дальнейшем будем называть световым
вектором, а интенсивность света будем
определять плотностью потока энергии
электрического поля волны, считая, что
интенсивность света пропорциональна
квадрату амплитуды светового вектора
.
Напомним вкратце основные закономерности распространения света.
Рис. 24.3
1. При падении световой волны на границу раздела двух сред она полностью либо частично отражается, причем падающий луч, отраженный луч и нормаль, опущенная в точку падения луча, лежат в одной плоскости.
2. Угол падения равен углу отражения (рис. 24.3).
Законы преломления
1. При прохождении световой волной границы раздела двух сред она меняет свое направление (преломляется), причем падающий и отраженный лучи лежат в одной плоскости с нормалью, опущенной в точку падения луча.
2. Отношение синуса угла падения к синусу угла преломления для данных двух сред не зависит от угла падения:
-
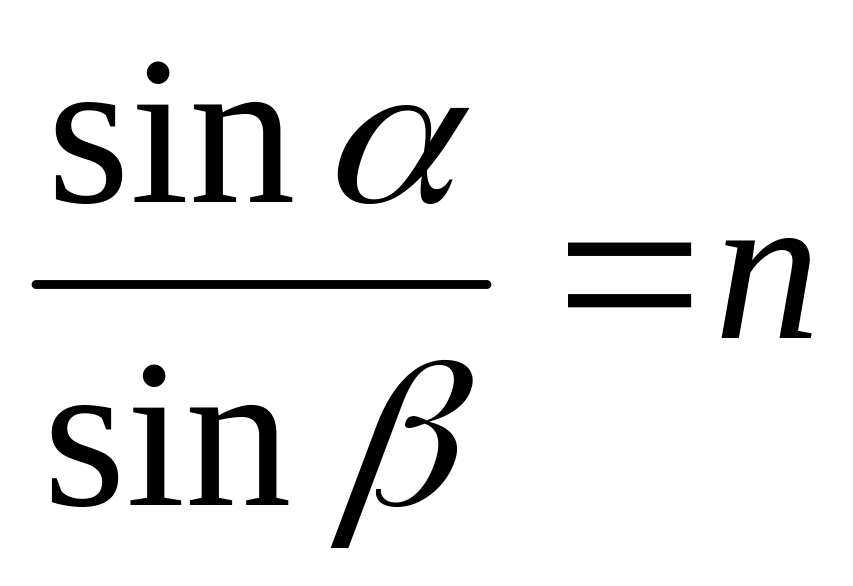,(24.19)
где n — относительный коэффициент преломления, равный отношению абсолютных (т.е. по отношению к вакууму) показателей преломления
.
Экспериментально
и теоретически было показано, что
абсолютный показатель преломления
ровен отношению скорости света в вакууме
к скорости света в данной среде, т.е.
.
Таким
образом, относительный показатель
преломления
.
Из закона преломления (24.16) следует: 1) если n > 1, то > , т.е. при переходе в оптически более плотную среду луч приближается к нормали (рис. 24.4, а); 2) если n < 1, то < , т.е. при переходе в оптически менее плотную среду (среду с меньшим показателем преломления) луч удаляется от нормали (рис. 24.4, б).
Рис. 24.4
.
Явление полного внутреннего отражения используется в таких элементах оптических приборов, как поворотная призма (рис. 24.5, а), оборотная призма (рис. 24.5, б), световод (рис. 24.5, в).
Рис. 24.5
Лекція 33.
25.1. Когерентные источники в оптике
Интерференцией называется явление наложения когерентных волн, в результате которого происходит пространственное распределение интенсивности — возникает картина интерференционных максимумов и минимумов.
Когерентными называются такие волны, которые обладают одинаковой частотой и не зависящей от времени разностью фаз. Именно это постоянство разности фаз и позволяет установится постоянной по времени интерференционной картине — правильному чередованию максимумов и минимумов. При наложении же некогерентных волн (даже одинаковой частоты) устойчивая интерференционная картина не образуется — из-за усреднения наблюдается лишь равномерно освещенное волновое поле.
Все естественные источники света состоят из большого числа микрочастиц (атомов, молекул), которые излучают световые волны независимо друг от друга и поэтому некогерентны. Свечение отдельного атома продолжается не более 10-8 с, причем различные атомы начинают излучать световые волны в разные моменты времени. В результате такого несогласования начальные фазы световых волн, испущенных различными атомами, случайным образом зависят от времени и, следовательно, такие волны будут некогерентны. Поэтому световые волны, идущие от двух независимых источников, не могут интерферировать между собой.
Рис. 25.1
Для получения когерентных световых волн (когерентных источников) используется следующий принцип: световые волны с помощью какого-нибудь устройства разделяются на две части, каждая из которых проходит различные пути, а затем с помощью соответствующих оптических приемов сводятся вместе и интерферируют. В качестве разделительных устройств в оптике используются бизеркала Френеля (рис. 25.1, а), зеркало Ллойда (рис. 25.1, б), бипризма Френеля (рис. 25.1, в), щели Юнга (рис. 25.1, г) и др. Следует отметить, что в случае зеркал Френеля оба когерентных источника мнимые, в зеркале Ллойда один из источников действительный, а в щелях Юнга оба источника действительны.