1.3. Расчёт напряжённости поля точечного заряда и электрического диполя

1.3.1. Напряженность поля точечного заряда

Рис. 1.1

Поместим в точку А (рис. 1.1), находящуюся на расстоянии r от заряда Q, пробный заряд q и найдем силу взаимодействия между ними по закону Кулона. Тогда напряженность поля, создаваемого зарядом Q на расстоянии r, на основании (1.2) и (1.5) может быть найдена по формуле

.

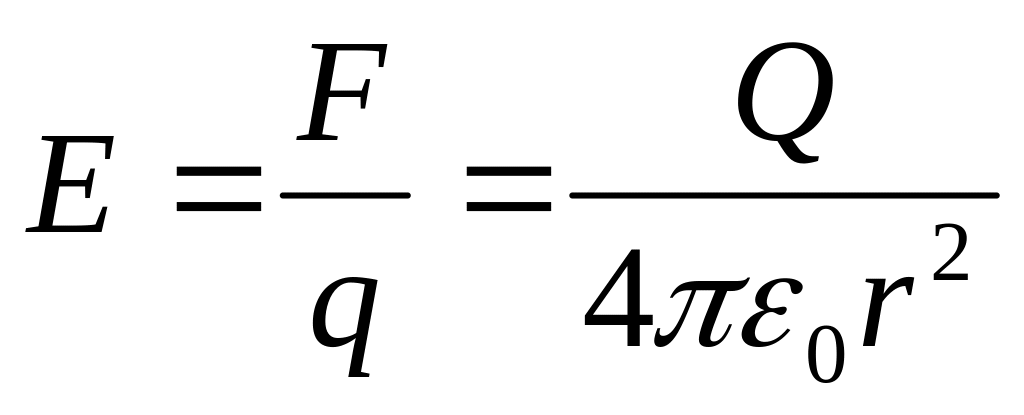(1.6)

Если заряд расположен в среде с диэлектрической проницаемостью , то

.

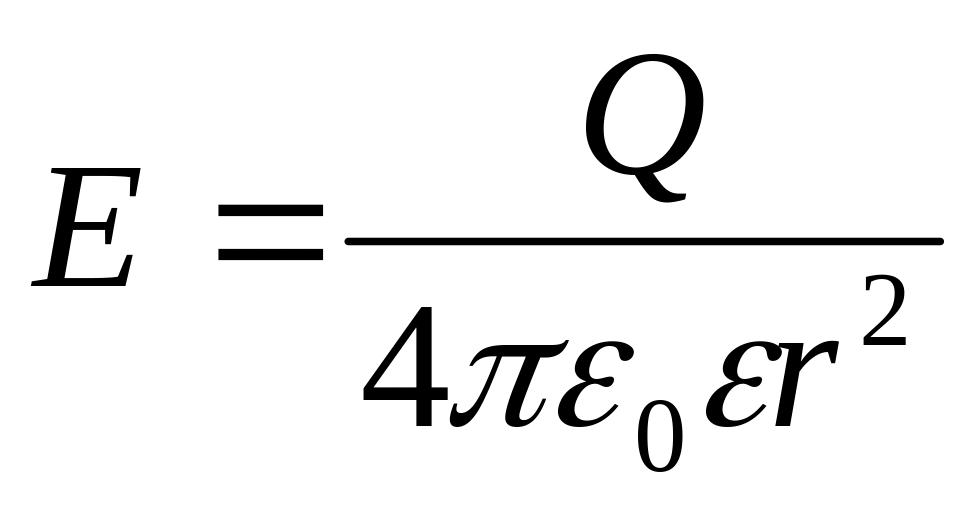(1.7)

1.3.2. Напряженность поля электрического диполя

Электрическим диполем называется совокупность двух точечных, одинаковых по величине, но противоположных по знаку зарядов, жестко закрепленных на расстоянии l друг от друга (рис. 1.2). Расстояние l называется плечом диполя, а вектор

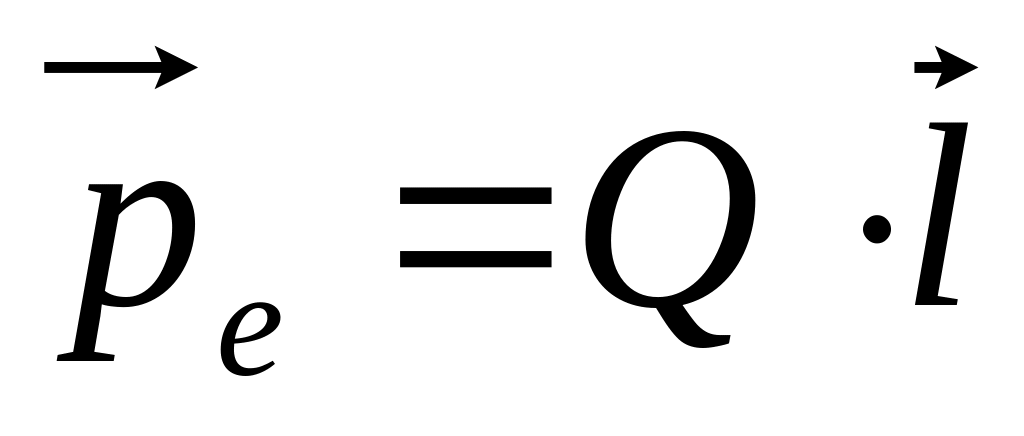
(1.8)

Рис. 1.2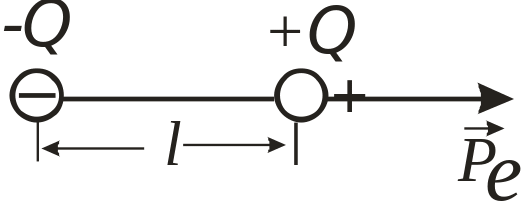

дипольным моментом (электрическим моментом диполя). Дипольный момент направлен вдоль оси диполя в сторону положительного заряда (рис. 1.2).Найдем теперь напряженность поля диполя, ограничиваясь случаем r>>l.

А. Напряженность поля в точке, находящейся на продолжении оси диполя

В соответствии с принципом суперпозиции напряженность поля в точке А (рис. 1.3)

Рис. 1.3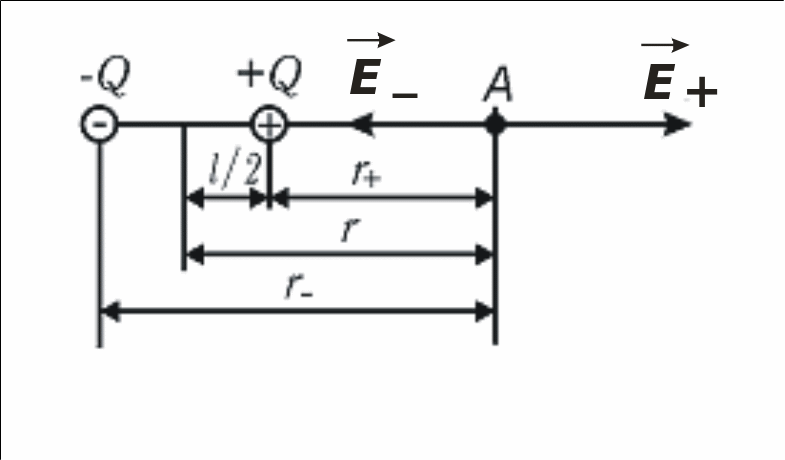

где и – напряженность поля, создаваемого соответственно зарядами +Q и -Q. Поскольку векторы и направлены в противоположные стороны, то модуль вектора будет , где в соответствии с (1.6) . Таким образом, .

Выражение в скобках преобразуем следующим образом. Из рис. 1.3 видно, что , где r – расстояние между точкой А и центром диполя. Далее имеем

.

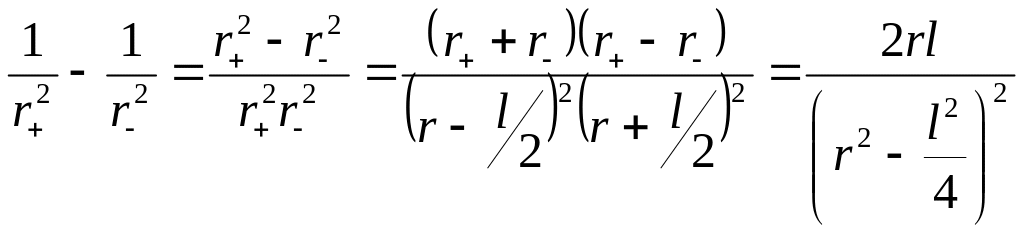Поскольку r>>l, то значением в знаменателе можно пренебречь, поэтому ;

.Так как Ql есть дипольный момент, то

Б. Напряженность поля на перпендикуляре оси диполя

Рис. 1.4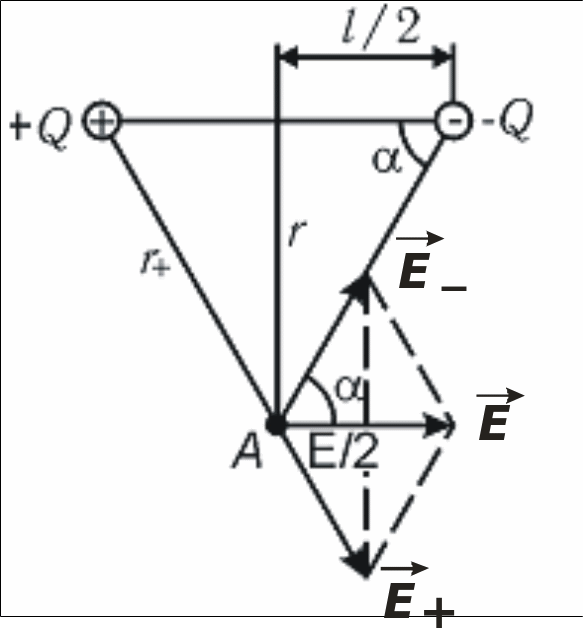

Из рис. 1.4 видно, что .Далее , ,

Следовательно, , где P_l=Ql – дипольный момент. Таким образом,

.

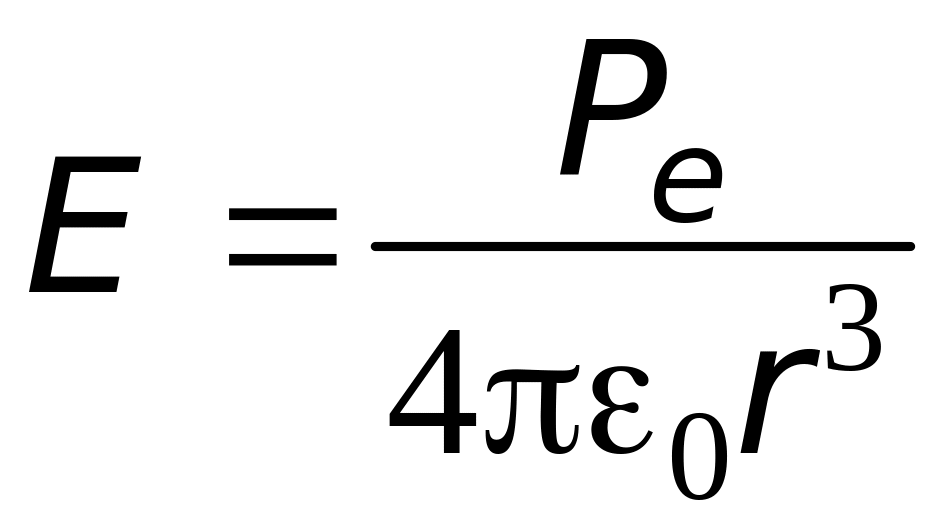(1.10)

Из сопоставления (1.9) и (1.10) видно, что напряженность поля на оси диполя в 2 раза больше, чем на перпендикуляре к его оси. Отметим также, что напряженность поля диполя убывает как 1/r^‑3, т.е. быстрее, чем для точечного заряда, где E1/r^‑2.

1.4. Силовые линии. Поток вектора напряженности. Теорема Остроградского-Гаусса

Силовой линией электростатического поля называется линия, касательная к которой в каждой точке совпадает с направлением вектора (рис. 1.5).

Рис. 1.5

Свойства силовых линий:

а) силовые линии электростатического поля не пересекаются;

б) силовые линии электростатического поля разомкнуты - они начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность).

Введем понятие потока вектора напряженности поля . По определению элементарный поток вектора напряженности через площадку dS

(1.11)

где  - угол между вектором и нормалью к площадке (рис. 1.6).

Выражение (1.11) можно представить как скалярное произведение

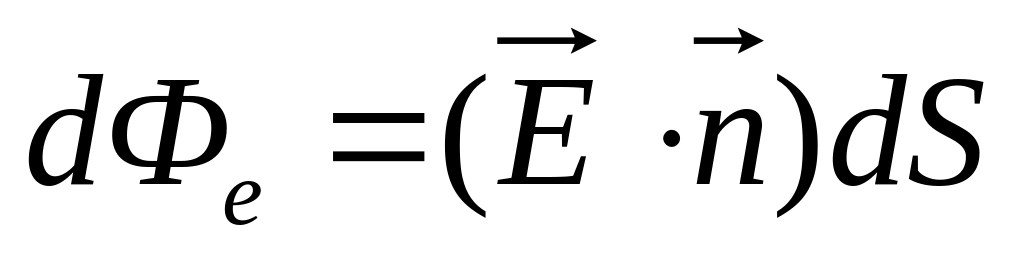
(1.12)

где – единичный вектор, совпадающий с нормалью.

Суммарный поток вектора напряженности через какую-либо поверхность можно найти интегрированием (11.12) для всей поверхности для замкнутой поверхности

Важнейшую роль в электростатике играет теорема Остроградского ‑ Гаусса, которая формулируется следующим образом: поток вектора напряженности через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, находящихся внутри этой поверхности:

, (1.13)

Рис. 1.6

Доказательство. Рассмотрим простейший случай, когда замкнутая поверхность представляет собой сферу, в центре которой находится точечный заряд +Q (рис. 1.7). Выделим на сфере элементарную площадку dS. Нормаль к этой площадке и вектор совпадают по направлению, поэтому .

Рис. 1.7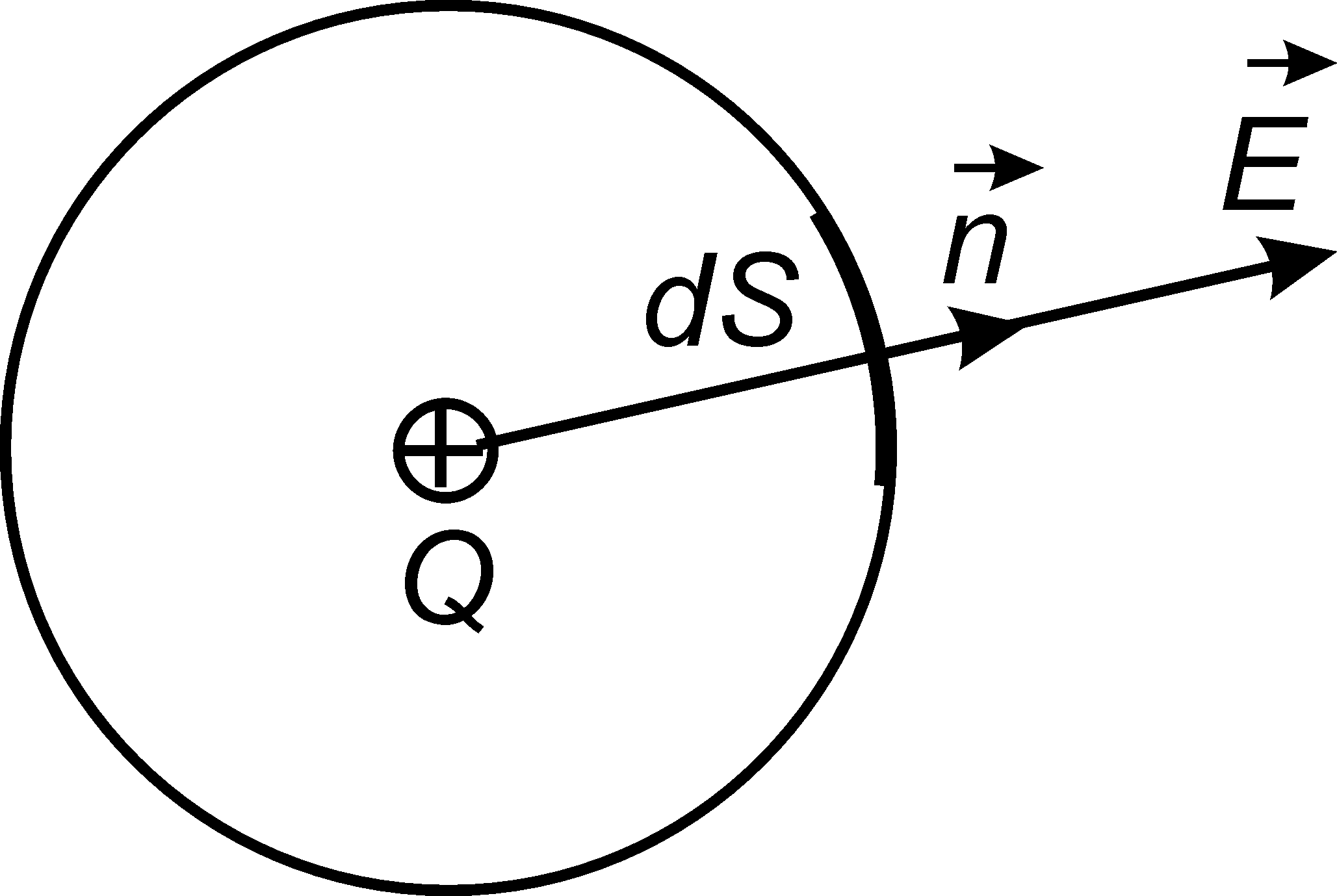

Преобразуем подынтегральное выражение в (1.13) следующим образом:

,

Принимая во внимание, что всюду на поверхности сферы E=const, и учитывая выражение (11.6), получим:

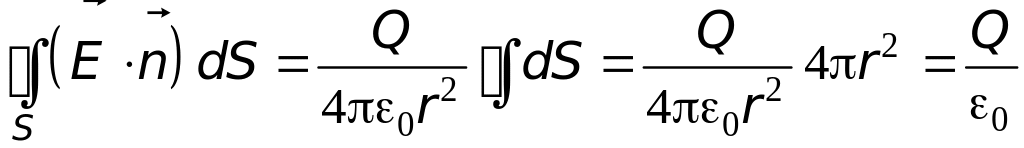
Теорема доказана для частного случая, когда внутри сферической поверхности имеется один заряд. Доказательство легко обобщается на случай произвольного числа зарядов и произвольной замкнутой поверхности.

В суммарном потоке, который создают заряды, расположенные за пределами замкнутой поверхности, можно выделить положительную и отрицательную части, которые взаимно компенсируются. Поэтому внешние по отношению к данной замкнутой поверхности заряды в теореме Остроградского – Гаусса не учитываются.

Теорема Остроградского-Гаусса связывает заряды с создаваемыми ими электрическими полями и отражает тот факт, что источником электростатического поля служат неподвижные электрические заряды.

Эта теорема тесно связана с законом Кулона: если справедлив закон Кулона, то справедлива и теорема Остроградского-Гаусса, и наоборот. Если бы в законе Кулона показатель степени хотя бы незначительно отличался от двух, т.е. F1/r^2+α, где α – сколь угодно малое число, то теорема Остроградского-Гаусса нарушалась бы. Справедливость теоремы Остроградского-Гаусса проверена на опыте с гораздо большей точностью, чем закон Кулона.