17.2. Сопоставление электрического и магнитного взаимодействий
ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ 1. Между двумя неподвижными точечными зарядами возникает сила электростатического взаимодействия, значение которой определяется законом Кулона: |
МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ 1.Между движущимися электрическими зарядами, кроме силы электрического взаимодействия, возникает сила магнитного взаимодействия: |
|||
|
(17.10) |
. |
(17.10а) |
|
2. Взаимодействие между неподвижными зарядами осуществляется через электростатическое поле, силовая характеристика которого – вектор напряженности : |
2. Магнитное взаимодействие движущихся электрических зарядов осуществляется через магнитное поле, силовая характеристика которого вектор магнитной индукции |
|||
|
(17.11) |
|
|
|
|
Или |
|||
|
|
|
(17.11а) |
|
3. На заряд, помещенный в электростатическое поле действует сила |
3. На заряд, движущийся в магнитном поле, действует сила, которая называется силой Лоренца. Из (17.11а) при Fm=FЛ следует |
|||
. |
(17.12) |
|||
|
|
|
(17.12а) |
|
|
|
или в векторной форме |
|
|
|
|
|
|
|
|
Из (17.12а) при q=1, v=1, sin = 1 следует B=FЛ, т.е. модуль вектора магнитной индукции численно равен силе Лоренца, действующей на единичный положительный заряд, движущийся с единичной скоростью в магнитном поле в направлении наибольшего действия силы. |
|||
4. Напряженность электростатического поля точечного заряда |
4. Вектор магнитной индукции, создаваемый движущимся электрическим зарядом |
|||
|
(17.13) |
|
|
|
|
Или |
|||
|
|
|
(17.13а) |
|
(Эта формула получается подстановкой (17.10) в (17.11)). |
(Эта формула получается подстановкой (17.10а) в (17.11а)). Формула (17.13а) называется формулой Лоренца. |
|||
5. Силовые линии электростатического поля разомкнуты: они выходят из положительного заряда и обрываются на отрицательном или уходят в бесконечность. |
5. Силовые линии магнитного поля замкнуты сами на себя. Этот факт установлен экспериментально. Например, силовые линии магнитного поля прямолинейного проводника с током имеют вид концентрических окружностей (рис. 17.2). |
|||
6. Характеристикой электростатического поля, не зависящей от свойств среды, служит вектор электростатического смещения |
6. Характеристикой магнитного поля, не зависящей от свойств среды, служит вектор напряженности магнитного поля |
|||
. |
(17.14) |
|
(17.14а) |
|
где – диэлектрическая проницаемость среды. |
где – магнитная проницаемость среды. |
|||
.
.
.
.
.
.
.
.
.
Рис. 17.2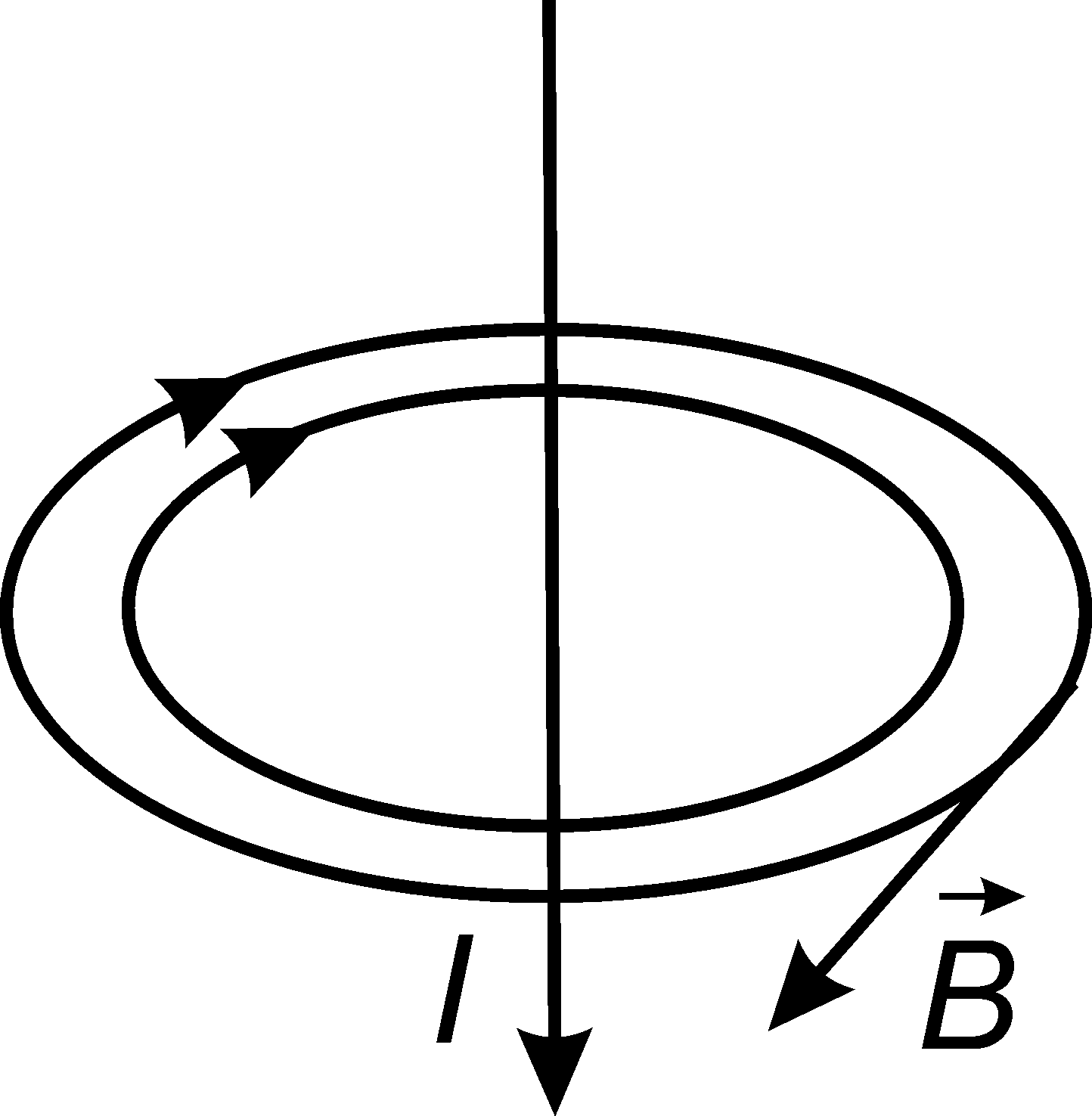
Вектор магнитной индукции движущегося заряда определяется формулой Лоренца (17.13а). Поскольку ток – это направленное движение зарядов, то каждый из них в некоторой точке пространства создает магнитное поле. Суммарное магнитное поле, создаваемое всеми зарядами, можно найти, исходя из принципа суперпозиции
,
где
–
вектор магнитной индукции, создаваемой
i-м
движущимся зарядом.
Согласно этим соображениям, найдем вектор магнитной индукции, создаваемый проводником с током произвольной формы (рис. 17.3).
Рис. 17.3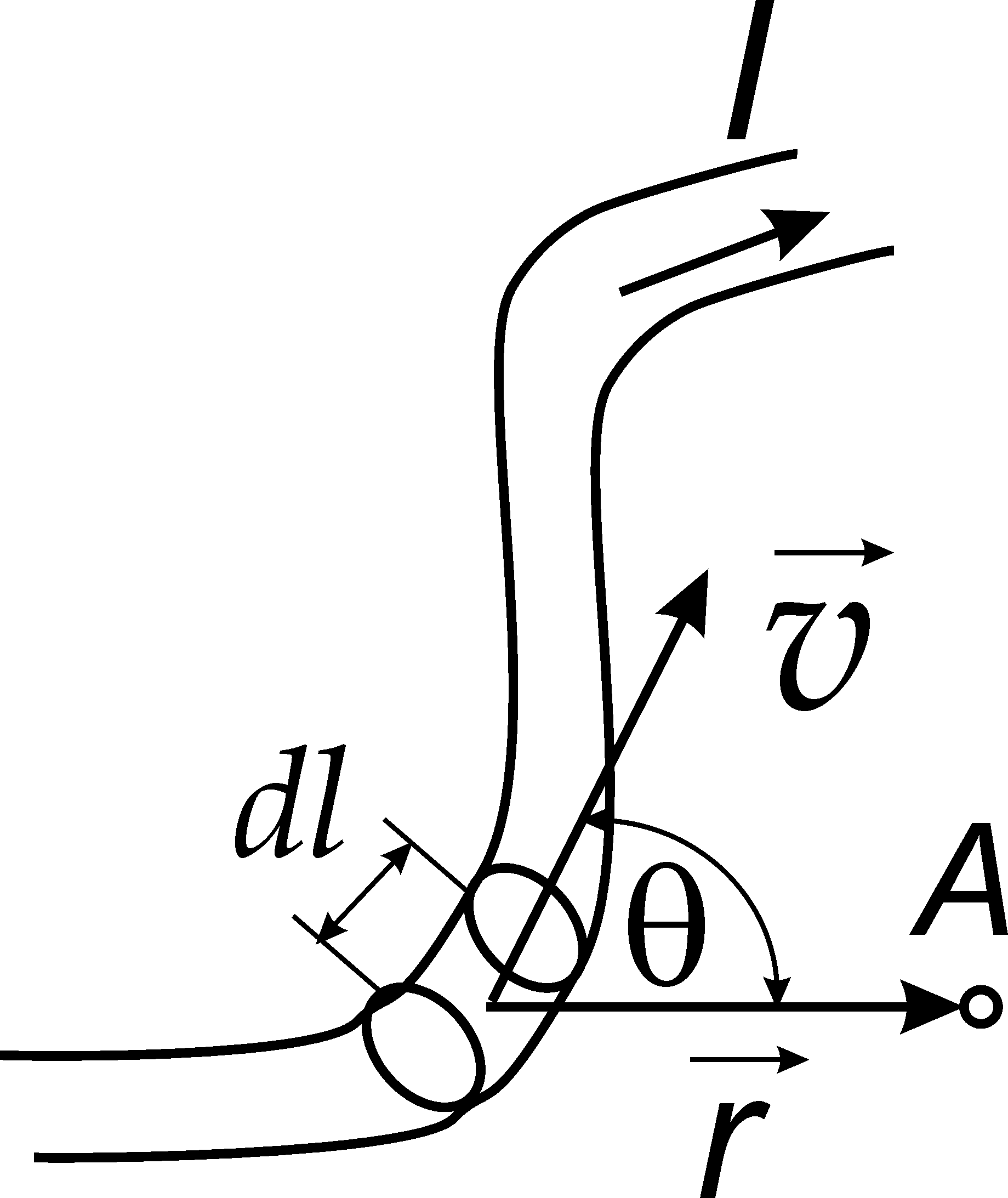
,
создает в точке A
магнитное поле с вектором индукции
,
значение которого можно найти с помощью
формулы Лоренца:
,
где 0 – магнитная проницаемость среды, в которой находится проводник.
Преобразуем dQv в формуле Лоренца следующим образом:
,
где I – сила тока в проводнике, а dl=vdt – элемент длины.
Таким образом,
-
,(17.15)
Для нахождения суммарной индукции B в точке A нужно продифференцировать выражение (17.15) по всей длине проводника:
-
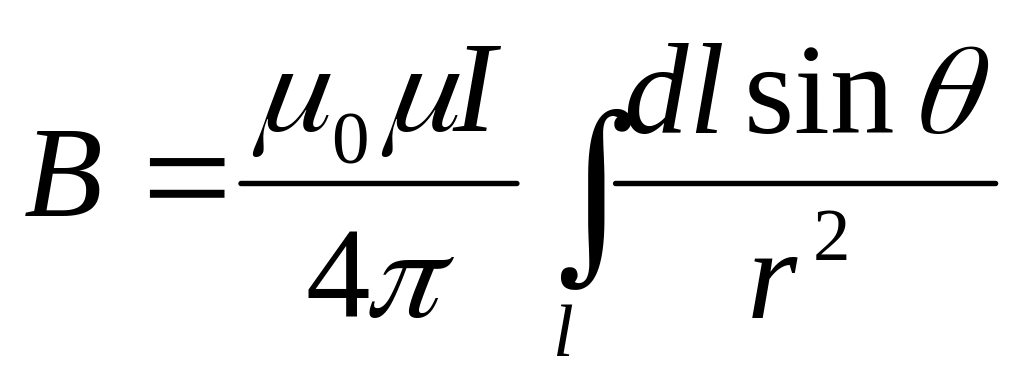.(17.16)
Поскольку
,
то напряженность магнитного поля
-
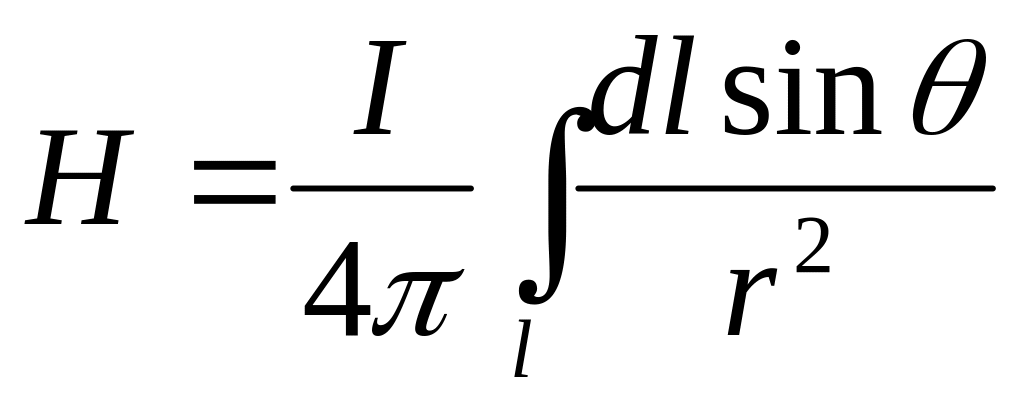.(17.17)
Формула (17.15) представляет собой закон Био-Савара-Лапласа. Этот закон позволяет рассчитать магнитные поля, создаваемые проводниками с током любой конфигурации.
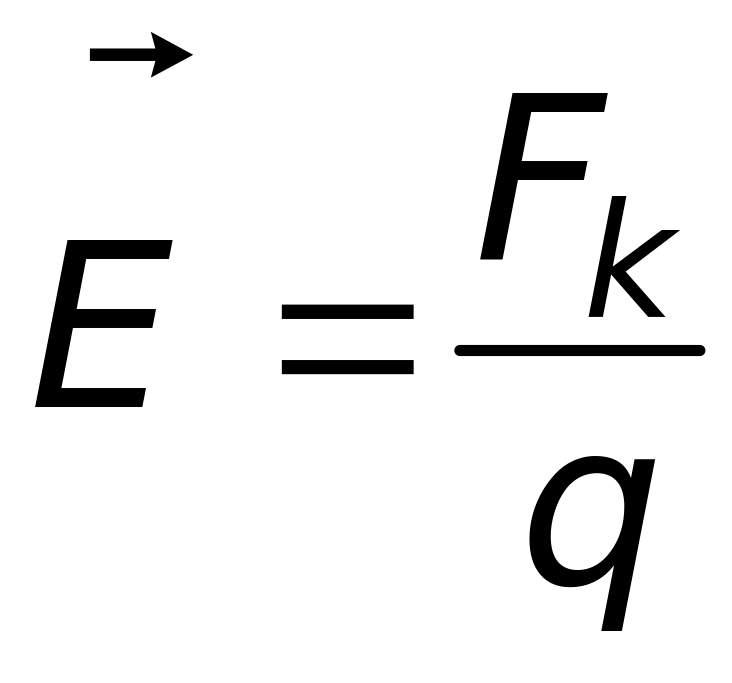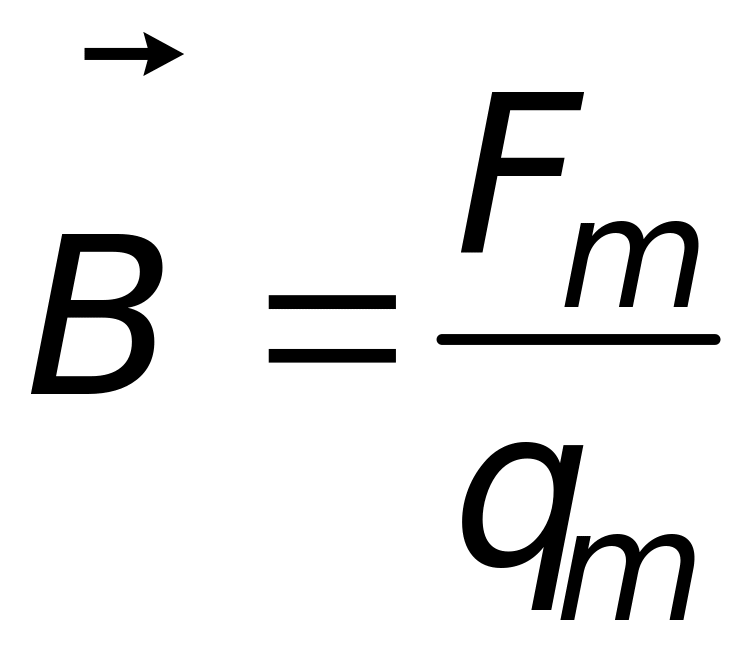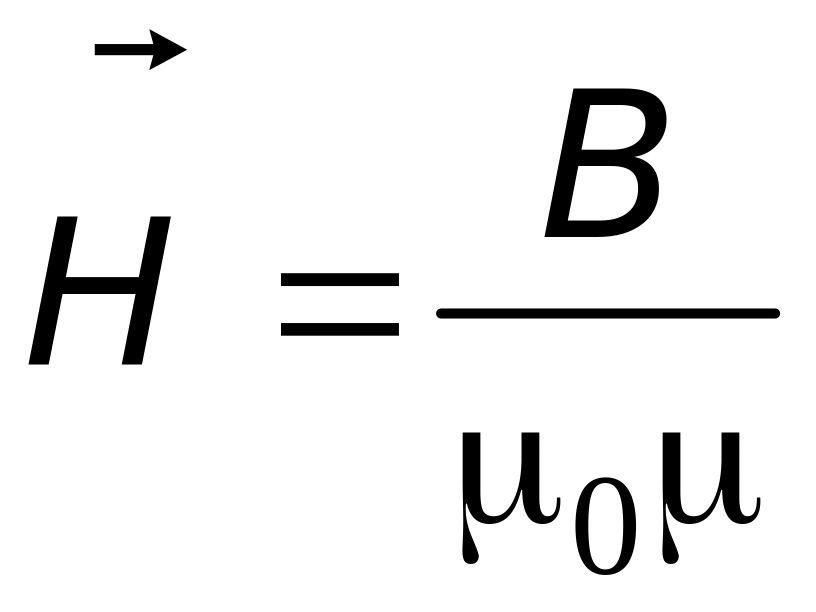