15.6. Правила Кирхгофа

Для расчета сложных цепей постоянного тока применяют правила Кирхгофа.

Первое правило Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.

.

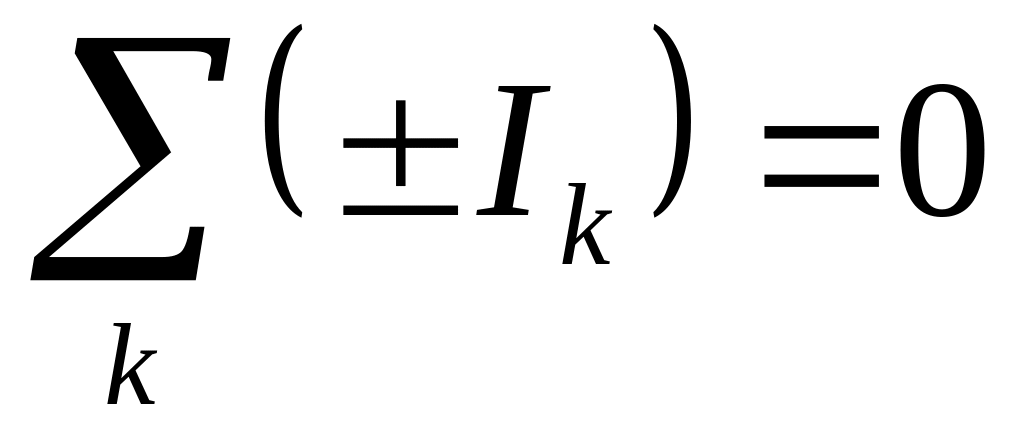(15.31)

Узлом называется точка цепи, где пересекаются три и более проводников. Ток берется со знаком "+", если он входит в узел; выходящий из узла ток берется со знаком "-".

Рис. 15.6

Для узла показанного, на рис. 15.6, первое правило Кирхгофа записывается в виде , или ,

т.е. сумма токов, входящих в узел, равна сумме токов, выходящих из него.

Первое правило Кирхгофа – следствие закона сохранения электрического заряда: заряды, попав в узел, никуда не исчезают и не накапливаются.

Второе правило Кирхгофа. Алгебраическая сумма падений напряжения в замкнутом контуре, выделенном из сложной цепи, равна алгебраической сумме ЭДС, включенных в этот контур:

.

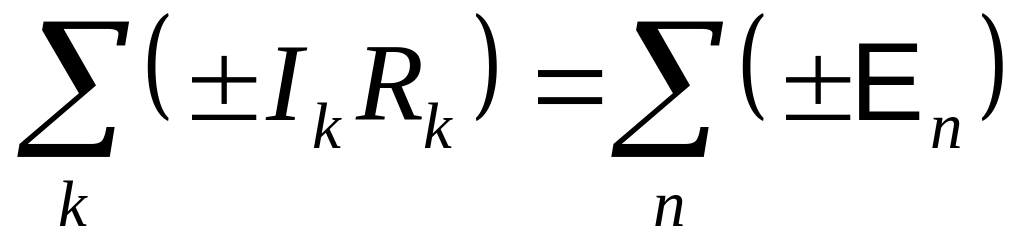(15.32)

Падение напряжения берется со знаком "+", если ток направлен в сторону обхода контура, и "-" в противном случае. ЭДС берется со знаком "+", если она действует в направлении обхода, и "-" – в противном случае. Направление обхода выбирается произвольно. Для определенности выберем направление обхода по часовой стрелке.

Запишем для примера второе правило Кирхгофа для контуров ABCFA и ABCDEFA (рис. 15.7):

контур ABCFA: I₁R₁ + I₂R₂= E ₁ – E₂;

контур ABCDEFA: I₁R₁ - I₃R₃= E ₁ – E₃.

В общем случае, когда в цепи имеется n узлов и m контуров, нужно составить n-1 уравнение по первому правилу Кирхгофа и m-1 уравнение по второму правилу.

Рис. 15.7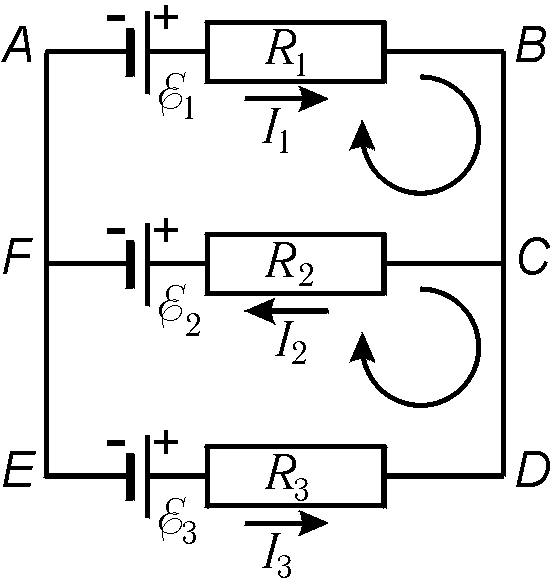

Лекція 25.

16. Контактные и термоэлектрические явления

16.1. Работа выхода

В состоянии равновесия любой металлический образец окружен тонким слоем электронов, вылетевших из металла в окружающее пространство. При этом заряженная положительно (вследствие вылета части электронов) поверхность металла и слой вылетевших электронов являются обкладками своеобразного конденсатора, между которыми существует разность потенциалов  . Для удаления электрона из металла его энергия должна быть достаточной для преодоления электрического поля поверхностного конденсатора W_кe.

Значение минимальной кинетической энергии электрона, достаточной для выхода его из металла, называют работой выхода и измеряют в несистемных единицах энергии – электрон-вольтах (1 эВ=1,610^‑19 Дж).

Значение работы выхода зависит как от рода металла, так и от состояния его поверхности.

16.2. Контактная разность потенциалов

Если два разнородных металлических проводника привести в контакт, то электроны получают возможность переходить из одного проводника в другой и обратно. Равновесное состояние такой системы наступит тогда, когда возникшая между металлами разность потенциалов прекратит перетекание электронов из одного металла в другой².

Величина контактной разности потенциалов определяется различием работ выхода и концентраций электронов в контактирующих металлах:

.

Получим выражение для контактной разности потенциалов.

Пусть (при равной концентрации электронов) работа выхода электрона из металла 1 больше, чем из металла 2. Тогда электроны будут чаще переходить из металла 2 в металл 1, чем обратно. В результате металл 1 зарядится отрицательно, а 2 – положительно и между ними возникнет контактная разность потенциалов  _A.

Рис. 16.1

Для того, чтобы найти контактную разность потенциалов _A подсчитаем работу по перенесению электрона по замкнутому контуру (рис. 16.1). Эта работа согласно (11.19) равна нулю:

,

где A₁₂ – работа по перемещению электрона из одного металла в другой; A₁ и A₂ – работа выхода электронов соответственно из первого и второго металлов. Отсюда

,

следовательно,

.

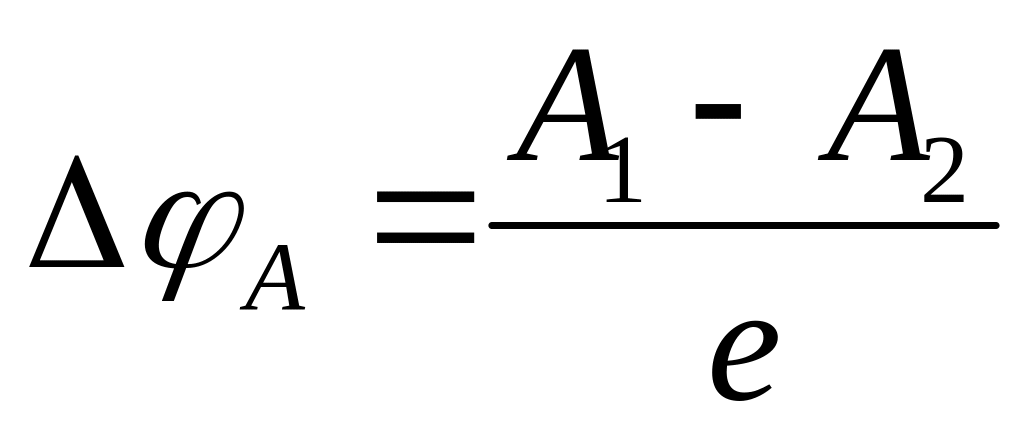(16.1)

Рассмотрим теперь вторую часть контактной разности потенциалов , связанную с различием концентраций электронов в металлах. Очевидно, что если n₂ > n₁, то переходы электронов из металла 2 в металл 1 будут происходить чаще, чем в обратном направлении. В результате металл 1 зарядится отрицательно, а металл 2 – положительно и возникшее электрическое поле прекратит дальнейшее перемещение электронов. В области контакта двух металлов электронный газ будет находиться в потенциальном (электростатическом) поле, поэтому для распределения концентрации электронов применима формула Больцмана

,

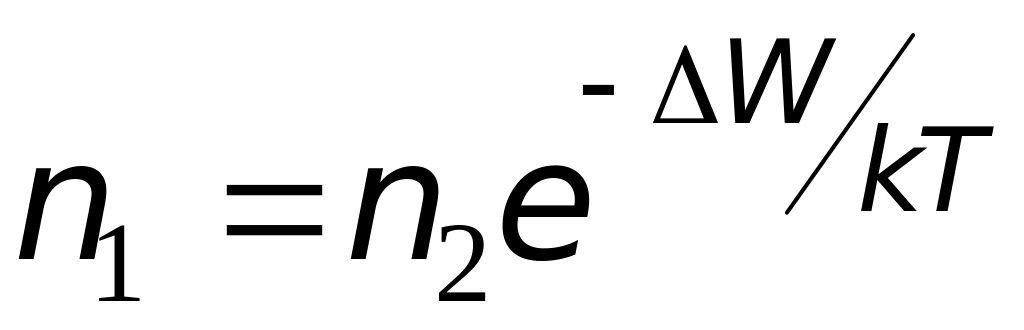(16.2)

где  W=e_n.

Из (16.2) следует

.

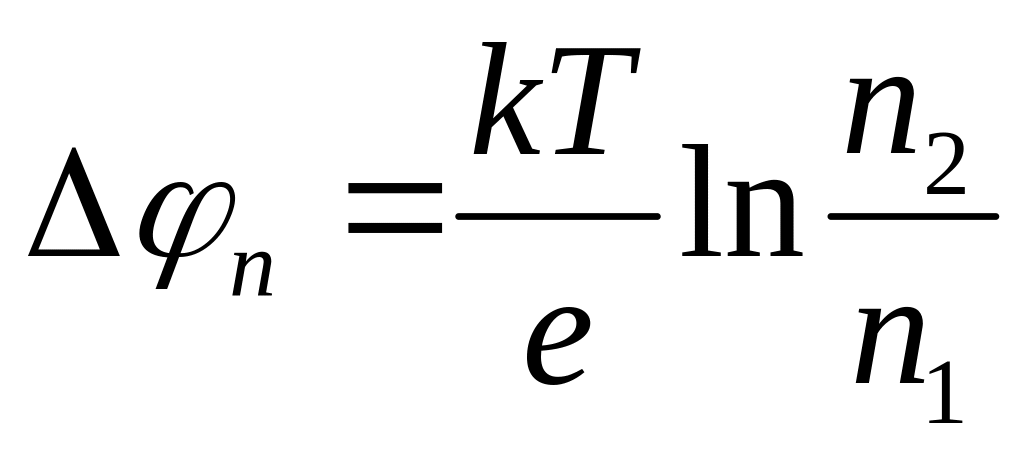(16.3)

Из (16.1) и (16.3) находим общее выражение для контактной разности потенциалов:

.

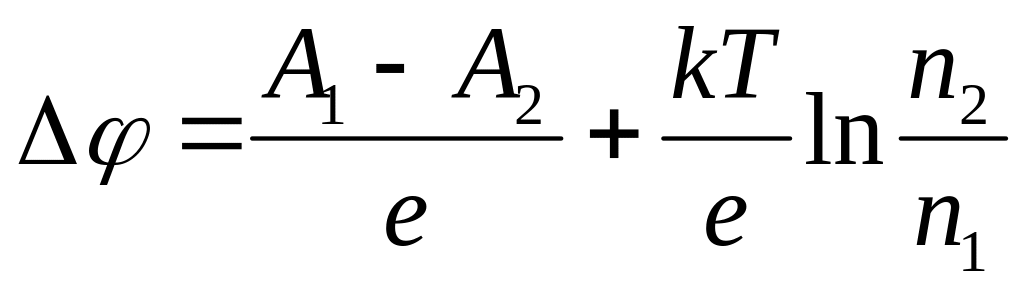(16.4)

Экспериментально существование контактной разности потенциалов установил А. Вольта, сформулировавший следующие законы.

1. Контактная разность потенциалов между двумя металлами зависит от их химической природы и температуры.

2. .Контактная разность потенциалов между концами цепи, состоящей из нескольких последовательно соединенных разнородных металлов, находящихся при одинаковых температурах, не зависит от свойств промежуточных проводников и равна

Рис. 16.2

контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников цепи:  = ₁₃ (рис. 16.2).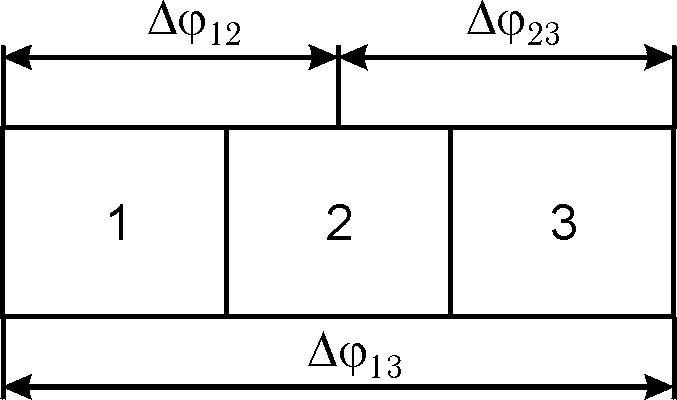

Действительно,

,

откуда

.