
- •1. Электростатическое поле в вакууме
- •1.1 Дискретность электрического заряда. Закон сохранения электрического заряда
- •1.2 Закон Кулона. Напряженность электрического поля
- •1.3. Расчёт напряжённости поля точечного заряда и электрического диполя
- •1.3.1. Напряженность поля точечного заряда
- •1.3.2. Напряженность поля электрического диполя
- •А. Напряженность поля в точке, находящейся на продолжении оси диполя
- •1.4. Силовые линии. Поток вектора напряженности. Теорема Остроградского-Гаусса
- •1.5. Применение теоремы Остроградского-Гаусса для расчета полей
- •1.5.1. Поле бесконечной равномерно заряженной плоскости
- •11.5.2. Поле двух бесконечных равномерно заряженных плоскостей
- •11.5.3. Напряженность поля бесконечной равномерно заряженной нити с линейной плотностью заряда
- •11.6. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора
- •11.7. Связь между напряженностью поля и потенциалом
- •2. Электростатическое поле в диэлектрике
- •2.1. Поляризация диэлектриков
- •2.2. Полярные и неполярные молекулы
- •2.2.1. Неполярная молекула во внешнем электростатическом поле
- •2.2.2. Полярная молекула во внешнем электростатическом поле
- •2.3. Классификация диэлектриков
- •2.4. Поляризованность. Вектор электрического смещения
- •2.4.1 Поляризованность
- •2.4.2. Связь между поляризованностью и поверхностной плотностью связанных зарядов
- •12.4.3. Связь между поляризованностью и напряжённостью поля
- •12.4.4. Вектор электрического смещения
- •12.4.5. Связь между векторами , и .
- •2.5. Нелинейные диэлектрики
- •2.5.1. Сегнетоэлектрики
- •2.5.2. Электреты
- •2.5.3. Пироэлектрики
- •3. Проводники в электростатическом поле
- •3.1. Условия на границе металл – вакуум
- •13.2. Напряжённость поля вблизи поверхности заряженного проводника
- •13.3. Электроёмкость уединённого тела и системы тел
- •13.3.1. Плоский конденсатор
- •13.3.2. Цилиндрический конденсатор
- •14. Энергия электростатического поля
- •14.1. Энергия системы точечных зарядов
- •14.2. Энергия заряженного проводника
- •14.3. Энергия заряженного конденсатора. Плотность энергии электростатического поля
- •15. Постоянный электрический ток
- •15.1. Сила и плотность тока
- •15.2. Условия существования тока. Сторонние силы. Эдс
- •15.3. Закон Ома
- •15.3.1. Закон Ома для неоднородного участка цепи
- •15.3.2. Закон Ома для полной цепи
- •15.3.3. Закон Ома для однородного участка цепи
- •15.3.4. Закон Ома в дифференциальной форме
- •15.4. Закон Джоуля-Ленца
- •15.4.1. Закон Джоуля-Ленца в интегральной форме
- •15.4.2. Закон Джоуля-Ленца в дифференциальной форме
- •15.5. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории
- •15.6. Правила Кирхгофа
- •16. Контактные и термоэлектрические явления
- •16.1. Работа выхода
- •16.2. Контактная разность потенциалов
- •16.3. Эффект Зеебека
- •16.4. Эффект Пельтье
- •17. Магнитное взаимодействие
- •17.1. Магнитное взаимодействие движущихся электрических зарядов
- •17.2. Сопоставление электрического и магнитного взаимодействий
- •17.4. Магнитное поля прямолинейного проводника с током
- •17.5. Магнитное поле кругового тока
- •17.6. Циркуляция вектора
- •17.17. Магнитное поле тороида, соленоида
- •17.8. Сила Лоренца
- •17.9. Эффект Холла
- •17.10. Сила Ампера
- •17.11. Поток вектора магнитной индукции
- •17.12. Магнитная цепь
- •17.13. Работа по перемещению проводника с током в магнитном поле
- •18.1. Эдс индукции. Правило Ленца
- •18.2. Фарадеевская трактовка явления электромагнитной индукции
- •18.3. Максвелловская трактовка явления электромагнитной индукции
- •18.4. Явления самоиндукции и взаимной индукции
- •18.5. Индуктивность тороида
- •18.6. Плотность энергии магнитного поля
- •18.7. Экстратоки замыкания и размыкания
- •18.8 Токи Фуко. Скин-эффект
- •20. Теория Максвелла
- •20.1. Ток смещения
- •20.2. Полная система уравнений Максвелла
- •19. Магнитные свойства веществ
- •19.1. Гипотеза Ампера
- •19.2. Магнитные моменты атомов
- •19.3. Вектор намагниченности
- •19.4. Слабо магнитные вещества
- •19.5. Сильномагнитные вещества
- •19.5.1. Ферромагнетики
- •19.5.2. Ферримагнетики
- •19.5.3. Антиферромагнетики
- •19.5.4. Магнитные материалы
- •21.14. Вынужденные электромагнитные колебания
- •21.14.1. Омическое сопротивление в цепи переменного тока
- •21.14.2. Индуктивность в цепи переменного тока
- •21.14.3. Емкость в цепи переменного тока
- •24.1. Уравнение плоской электромагнитной волны
- •24.2. Вектор Умова – Пойнтинга
- •24.3. Особенности распространения электромагнитных волн
- •24.4. Световые волны
- •Законы преломления
- •25.1. Когерентные источники в оптике
- •25.2. Расчет интерференционной картины от двух когерентных источников
- •25.3. Интерференция в тонких пленках
- •25.4. Стоячие волны
- •25.5. Интерферометры
- •26.1. Принцип Гюйгенса-Френеля. Расчет дифракционной картины методом зон Френеля
- •26.2. Дифракция сферических волн (дифракция Френеля)
- •26.3. Дифракция плоских волн (Дифракция Фраунгофера)
- •26.4. Дифракционная решетка
- •27.1. Общие представления о поляризации световых волн
- •27.2. Поляризация света при отражении и преломлении
- •27.3. Двойное лучепреломление
- •27.4. Поляризационные приборы
- •27.5. Закон Малюса
- •27.6. Интерференция поляризованных лучей
- •27.7. Искусственная оптическая анизотропия
- •27.8. Вращение плоскости поляризации (оптическая активность)
- •27.9. Оптические и электрооптические свойства жидких кристаллов
- •28.1. Фазовая и групповая скорости света
- •28.2. Элементарная классическая теория дисперсии
- •28.3. Поглощение света
- •28.4. Рассеяние света
15.3.2. Закон Ома для полной цепи
При
обходе полной цепи начальная и конечная
точки совпадают, поэтому
![]() ;
;
-
 E
.
E
.(15.11)
Здесь под R0 следует понимать сумму внешнего R и внутреннего r сопротивлений. Произведя в (15.11) замену R0=R+r, получим закон Ома для полной цепи:
-
I= E /(R+r)
(15.12)
15.3.3. Закон Ома для однородного участка цепи
Однородным
называется участок цепи, не содержащий
источника ЭДС, т.е. в формуле (15.10) нужно
положить E
=0.
Тогда
![]() .
.
В данном случае падение напряжения совпадает с разностью потенциалов U= 1 - 1, т. е.
-
 ,
,(15.13)
что также совпадает с (15.9).
Формулы (15.9) и (15.13) представляют закон Ома в интегральной форме.
15.3.4. Закон Ома в дифференциальной форме
Рис. 5.3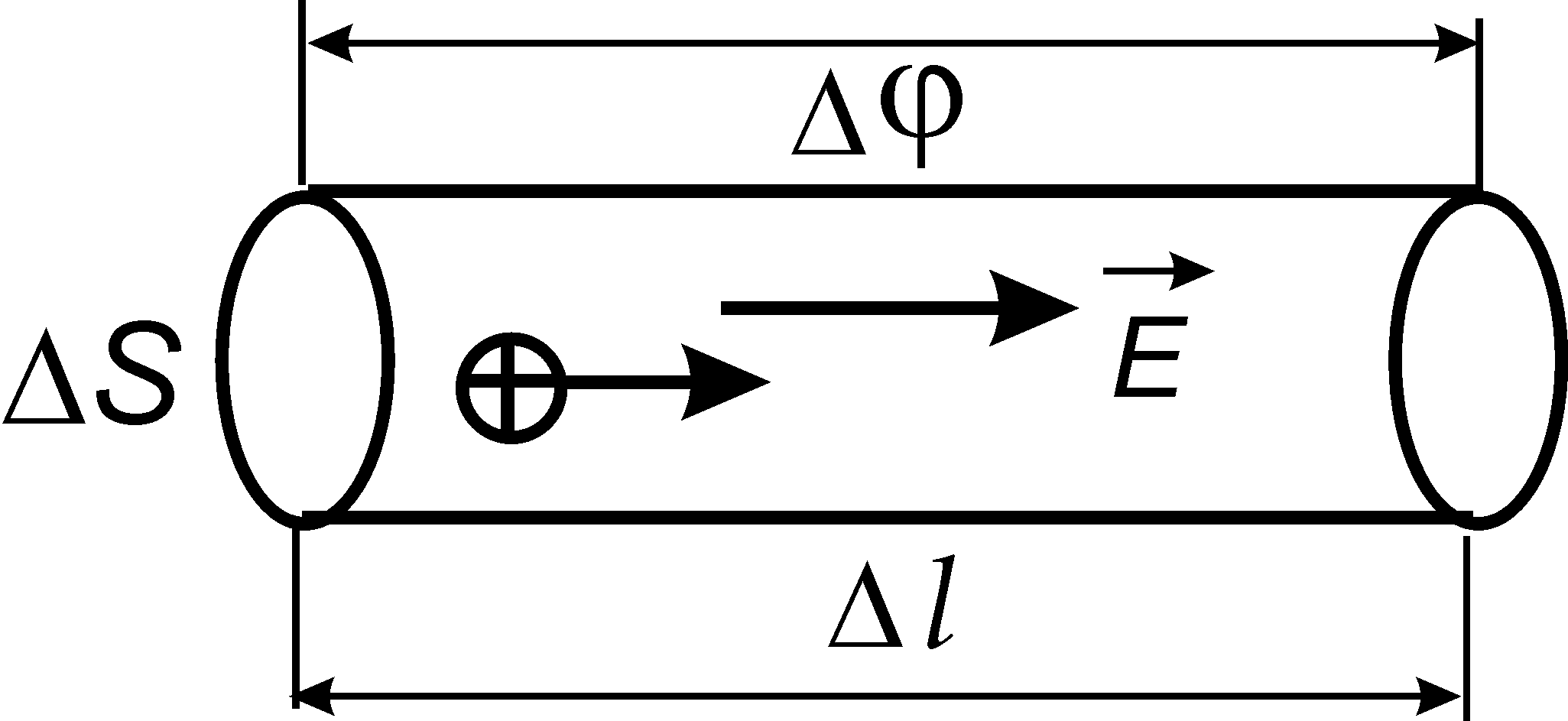
![]() ,
где –
удельное сопротивление проводника.
Разность потенциалов на концах цилиндра
.
Тогда закон Ома (см. (15.9)) запишем в виде
,
где –
удельное сопротивление проводника.
Разность потенциалов на концах цилиндра
.
Тогда закон Ома (см. (15.9)) запишем в виде
![]() или
.
или
.
С учетом (11.30) последнее выражение можно преобразовать к виду
-
 .
.(15.14)
Величина,
обратная удельному сопротивлению,
называется удельной проводимостью:
![]() .
.
Тогда
закону Ома в дифференциальной форме
(15.4) можно придать вид
![]()
15.4. Закон Джоуля-Ленца
15.4.1. Закон Джоуля-Ленца в интегральной форме
Джоуль и независимо от него Ленц экспериментально установили, сто количество теплоты, выделенной в проводнике сопротивлением R за время dt, пропорционально квадрату силы тока, сопротивлению и времени:
-
 .
.(15.16)
Формула (15.16) представляет закон Джоуля-Ленца в интегральной форме.
15.4.2. Закон Джоуля-Ленца в дифференциальной форме
Выделим,
как и ранее, внутри проводника элементарный
цилиндрический объем (рис. 15.3). Заменим
в (15.16)
![]() .
Тогда
.
Тогда![]() где V= lS –
объем проводника. Введем в рассмотрение
удельную мощность теплоты
где V= lS –
объем проводника. Введем в рассмотрение
удельную мощность теплоты
-
 [Дж/м3с
= Вт/м3].
[Дж/м3с
= Вт/м3].(15.18)
Удельная мощность теплоты численно равна количеству теплоты, выделенной в единице объема проводника за единицу времени. Другими словами – это тепловая мощность, развиваемая в единице объема. С учетом (15.18) выражению (15.17) можно придать вид
![]() .
.
-
Поскольку
 ,
то
,
то

(15.19)
или
 .
.(15.20)
Формулы (15.19) и (15.20) представляют закон Джоуля-Ленца в дифференциальной форме.
Лекція 24.
15.5. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории
В классической электронной теории металлов принимается следующая модель.
1. Носителями тока в металлах являются свободные электроны.
2. Свободные электроны образуют электронный газ, который по своим свойствам аналогичен идеальному газу. Имеется лишь одно различие: электроны при своем движении сталкиваются не между собой, а с ионами кристаллической решетки.
3.
Под действием электрического поля
электроны наряду с хаотическим движением
со скоростью
![]() начинают двигаться направлено со
скоростью
начинают двигаться направлено со
скоростью
![]() .
При этом скорость направленного движения
значительно меньше скорости хаотического
движения
.
При этом скорость направленного движения
значительно меньше скорости хаотического
движения
-
 .
.(15.21)
Найдем скорость направленного движения электронов. Предположим, что в момент времени t=0 скорость направленного движения электронов u0=0. Под действием силы F=eE электрон в соответствии со вторым законом Ньютона начинает двигаться ускоренно:
![]() .
.
Скорость направленного движения электрона
-
 .
.(15.22)
Рис. 15.4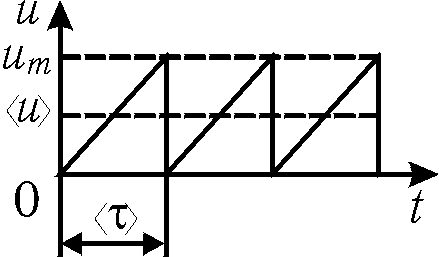
Среднее время между двумя последовательными столкновениями электрона
-
 ,
,(15.23)
где
![]() –
средняя длина свободного пробега
электрона;
–
средняя длина свободного пробега
электрона;
![]() –
среднее значение его скорости, которая
является векторной суммой скоростей
хаотического и направленного движений.
–
среднее значение его скорости, которая
является векторной суммой скоростей
хаотического и направленного движений.
В силу неравенства (15.21) скоростью направленного движения можно пренебречь, поэтому
-
 .
.(15.24)
Заменив в формуле (15.22) время t на , найдем максимальную скорость направленного движения электрона
-
 .
.(15.25)
Средняя скорость направленного движения электрона
-
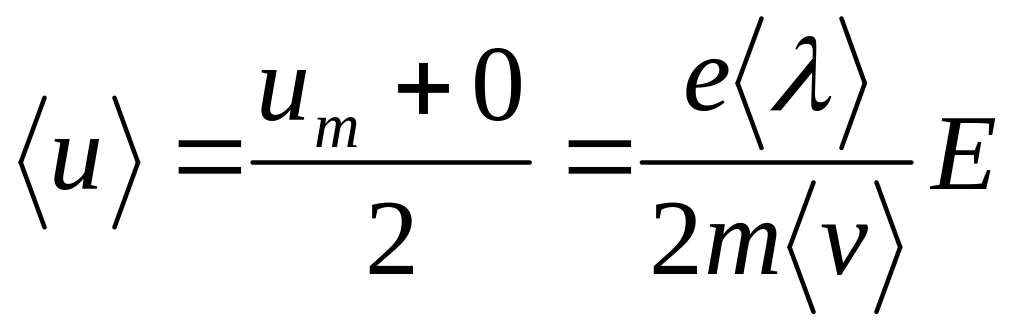 .
.(15.26)
Подставим (15.26) в выражение для плотности тока (15.3):
-
 .
.(15.27)
Из сопоставления (15.27) и (15.15) видно, что удельная проводимость металла
-
 .
.(15.28)
Тем самым удалось не только теоретически обосновать закон Ома, но и выразить удельную проводимость и, следовательно, удельное сопротивление
-
 .
.(15.29)
через характеристики электронного газа.
Исходя из представлений классической электронной теории металлов, получим теперь закон Джоуля–Ленца.
К
концу свободного пробега электрон
обладает кинетической энергией
направленного движения
![]() .
Эту энергию электрон полностью передает
иону кристаллической решетки при
столкновении с ним. Множество таких
столкновений приводит к выделению
джоулевой теплоты. Если концентрация
электронов n,
и каждый из них сталкивается
.
Эту энергию электрон полностью передает
иону кристаллической решетки при
столкновении с ним. Множество таких
столкновений приводит к выделению
джоулевой теплоты. Если концентрация
электронов n,
и каждый из них сталкивается
![]() раз за 1 с,
то в единичном объеме проводника
выделиться мощность
раз за 1 с,
то в единичном объеме проводника
выделиться мощность
 .
.
Подставляя сюда значение максимальной скорости направленного движения электрона из (15.25) и учитывая, что среднее число столкновений за 1 с
![]() ,
,
получаем закон Джоуля–Ленца
-
 .
.(15.30)
Из сопоставления (15.30) и (15.20) находим такое же выражение для удельной теплопроводности, как и в законе Ома (см. (15.28)).
Несмотря
на очевидные успехи классической
электронной теории металлов, она, тем
не менее, столкнулась с рядом трудностей.
В частности классическая теория
неправильно предсказывает зависимость
сопротивления металла от температуры.
Анализ выражения (15.29) показывает, что
от температуры зависит лишь скорость
хаотического движения. При этом (см.
формулу (8.18))
![]() ,
следовательно, удельное сопротивление
,
следовательно, удельное сопротивление
![]() .
Между тем опыт показывает, что
линейно зависит от температуры
.
Между тем опыт показывает, что
линейно зависит от температуры![]() ,
,
Рис. 15.5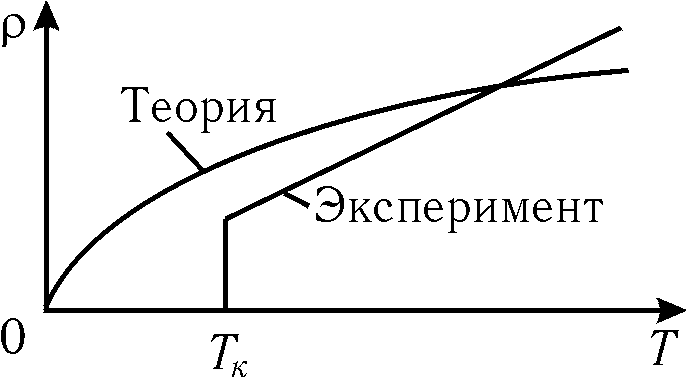
Трудности классической теории были устранены квантовой теорией электропроводности (§ 31.3).
