14.3. Энергия заряженного конденсатора. Плотность энергии электростатического поля

Для вычисления энергии заряженного конденсатора воспользуемся формулами (14.5) – (14.7), заменив  на разность потенциалов между обкладками конденсатора U=__. Тогда

,	(14.8)
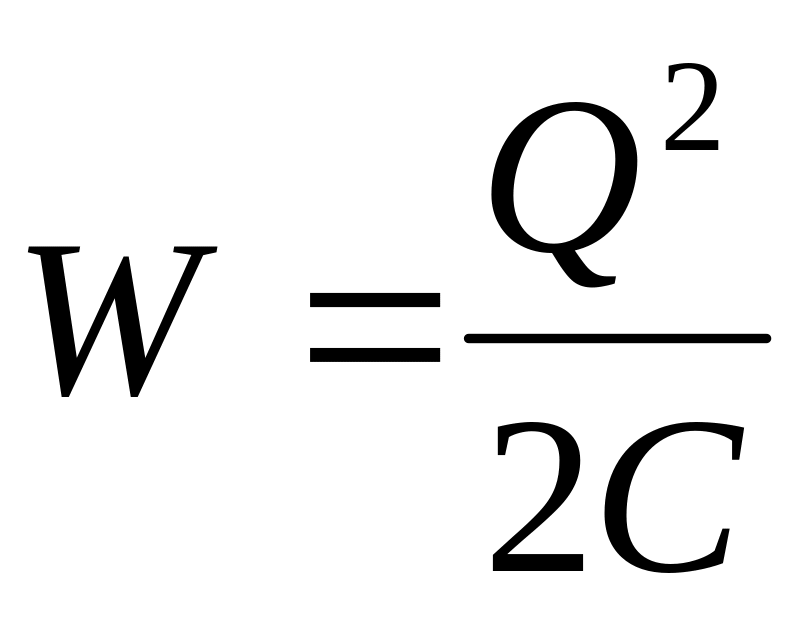
	(14.9)
	(14.10)

Дальнейшее рассмотрение проведём, основываясь на формуле (14.9). Представим заряд конденсатора как Q=S, где  – поверхностная плотность заряда, а S – площадь обкладки конденсатора. Воспользовавшись далее выражением для ёмкости плоского конденсатора (13.7), представим (14.9) в виде

,

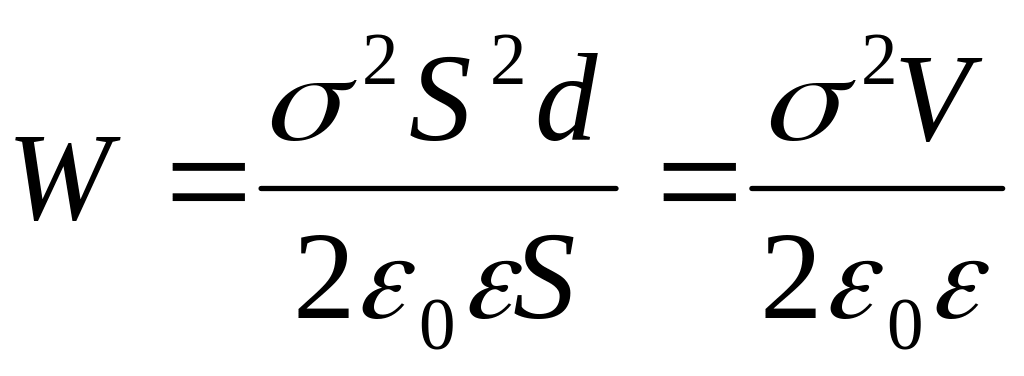(14.11)

где V=Sd – объём конденсатора.

С помощью (11.15) выразим поверхностную плотность заряда  через напряжённость поля E и подставим полученное выражение в (14.11). В результате получим

,

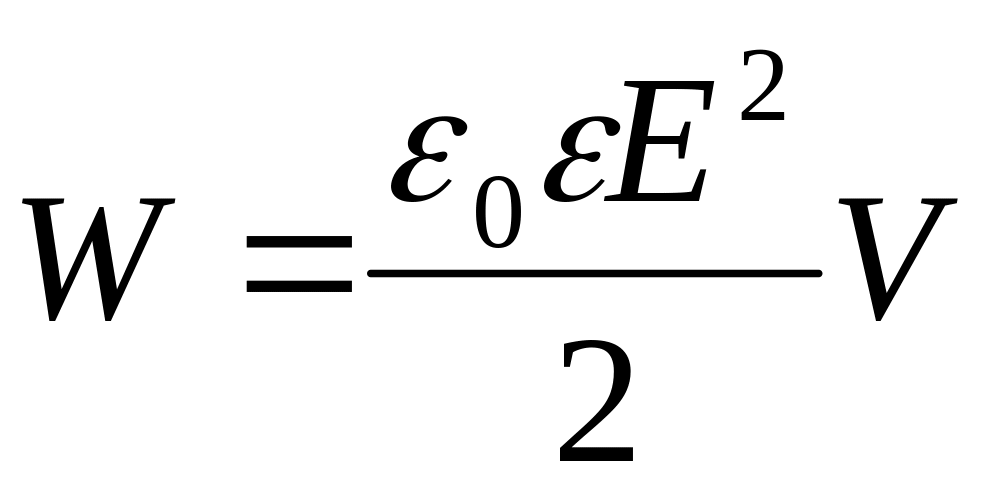(14.12)

В формуле (14.9) энергия заряженного конденсатора выражена через заряд на его обкладках и ёмкость. В формуле (14.12) энергия конденсатора выражена через напряжённость электростатического поля, сосредоточенного между его обкладками. В связи с этим возникает принципиальный вопрос о том, что служит носителем энергии конденсатора: заряды или электростатическое поле. Этот вопрос – центральный в длительной дискуссии между сторонниками дальнодействия и близкодействия.

Сторонники дальнодействия отдавали предпочтение формуле (14.9), рассматривая её как потенциальную энергию взаимодействия двух тел. Приверженцы этой теории отвергали возможность осуществления взаимодействия посредством поля.

Сторонники теории близкодействия (полевой теории) считали, что энергия конденсатора есть энергия электростатического поля (формула (14.2)). Эта энергия "размазана" по всему объёму конденсатора и, следовательно, можно говорить об объёмной плотности энергии:

[Дж/м³] или , С учётом (12.11) формулу (14.13) можно представить в виде

(14.14)

В рамках электростатики решить вопрос, что является носителем энергии – заряды или поле, невозможно, поскольку неподвижные заряды и создаваемое ими электростатическое поле неотделимы друг от друга. При изучении переменных электрических и магнитных полей оказалось, что электромагнитное поле может отрываться от зарядов, существуя независимо от них. Это и есть решающий аргумент в пользу теории близкодействия (полевой теории).

Лекція 23.

15. Постоянный электрический ток

15.1. Сила и плотность тока

Электрическим током называют упорядоченное (направленное) движение заряженных микрочастиц или заряженных макроскопических тел. За направление тока принимают направление движения положительных зарядов; если ток создается отрицательно заряженными частицами (например, электронами), то направление тока противоположно направлению движения частиц. Различают ток проводимости (направленное движение заряженных частиц внутри макроскопического тела) и конвекционный (движение заряженного тела как целого). В дальнейшем будем рассматривать лишь ток проводимости.

Количественно электрический ток характеризуется скалярной величиной силой тока I и векторной величиной – плотностью электрического тока .

Сила тока численно равна заряду, прошедшему через поперечное сечение проводника за единицу времени:

.

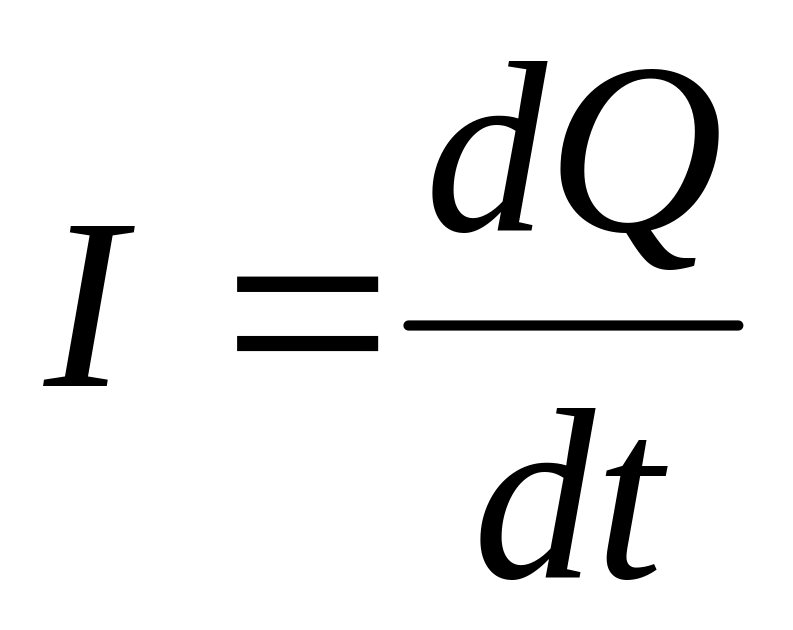(15.1)

Сила тока измеряется в амперах (определение дано во введении).

На разных участках поперечного сечения проводника за одно и то же время может протекать различный по величине заряд. Для учета этого обстоятельства вводят понятие вектора плотности тока. Вектор плотности тока численно равен силе тока, протекающего через единичное поперечное сечение проводника:

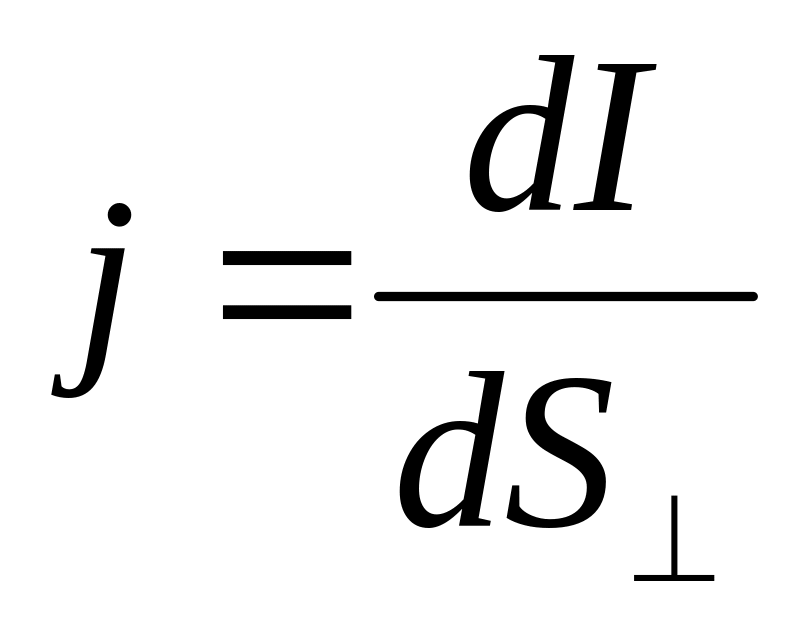[А/м2],

(15.2)

где знак "" обозначает, что площадка ориентирована перпендикулярно к направлению тока. Направление вектора совпадает с направлением движения положительных зарядов.

Найдем выражение для вектора плотности тока в металлах, у которых носителями тока являются свободные электроны. Под действием электрического поля электроны в металле движутся направлено со средней скоростью . За единицу времени через единичную площадку поперечного сечения проводника пройдет n электронов, где n – число электронов в единице объема (концентрация). При этом будет перенесен заряд en . Следовательно плотность тока

.

(15.3)