13.2. Напряжённость поля вблизи поверхности заряженного проводника

Рис. 13.3

Для расчёта напряженности поля вблизи поверхности заряженного проводника воспользуемся теоремой Остроградского-Гаусса. Выделим на поверхности проводника элементарную площадку S, а замыкающую поверхность выберем в виде цилиндра, боковая поверхность которого совпадает с линиями напряжённости (рис. 13.3).

Поток вектора через поверхность цилиндра представим в виде .

Поток через основание цилиндра S₁ равен нулю (_s1=0), поскольку внутри проводника поля нет. Поток через основание S₂: . Поток через боковую поверхность равен нулю, так как внутри проводника поля нет, а за его пределами силовые линии "скользят" вдоль его боковой поверхности, не пересекая её. Итак, полный поток через поверхность цилиндра =ES₂. Этот поток по теореме Остроградского-Гаусса пропорционален заряду, находящемуся внутри цилиндра . Вблизи поверхности проводника силовые линии приблизительно параллельны друг другу, поэтому боковая поверхность фигуры, показанной на рис. 13.3, не очень отличается от цилиндрической. В этом случае S₂S, поэтому

.

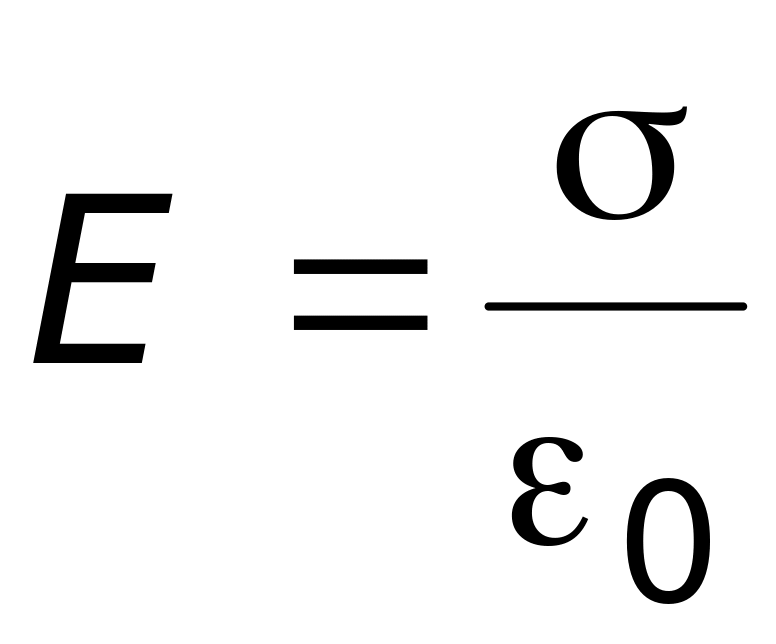(13.1)

Если проводник помещён в среду с диэлектрической проницаемостью , напряжённость поля вблизи его поверхности

.

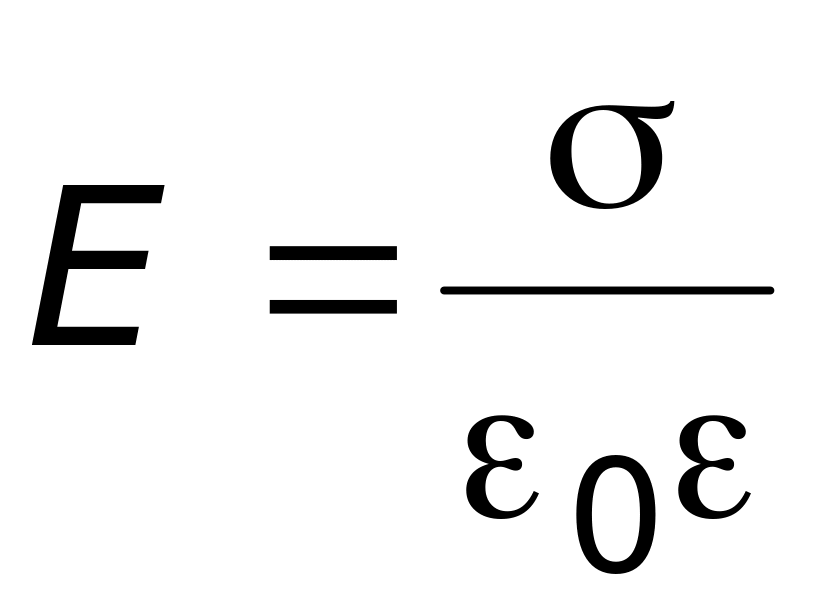(13.2)

Лекція 22.

Енергія системи точкових зарядів, зарядженого провідника, конденсатора. Густина енергії електростатичного поля.

13.3. Электроёмкость уединённого тела и системы тел

Для того чтобы зарядить проводник, следует перенести на его поверхность некоторый электрический заряд. Для перенесения очередной порции заряда необходимо совершить определённую работу против сил электрического поля, создаваемого ранее накопленными зарядами. Поскольку электрическое поле потенциально, то затраченная на перенос заряда работа превращается в потенциальную энергию заряженного проводника, определяемую его потенциалом . Таким образом, потенциал проводника линейно связан с его зарядом:

.

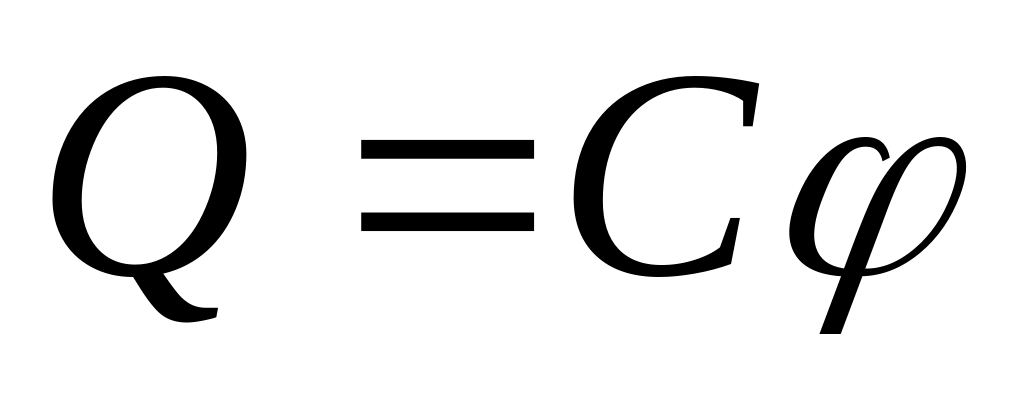(13.3)

где С – характерная для данного проводника константа, называемая электроёмкостью.

Электроёмкость проводника зависит только от его формы, размеров и диэлектрической проницаемости окружающей среды и не зависит от величины заряда и электропроводности проводника.

Электроёмкость численно равна заряду, который необходимо сообщить проводнику, чтобы его потенциал изменился на единицу:

.

(13.4)

Единица ёмкости в СИ – фарад. Один фарад – это ёмкость такого проводника, которому необходимо сообщить заряд в 1 Кл, чтобы изменить его потенциал на 1 В: 1 Ф = Кл/В.

Уединённый проводник имеет относительно небольшую ёмкость. Значительно большую ёмкость имеет система двух проводников, т.е. конденсатор. Ёмкость конденсатора

.

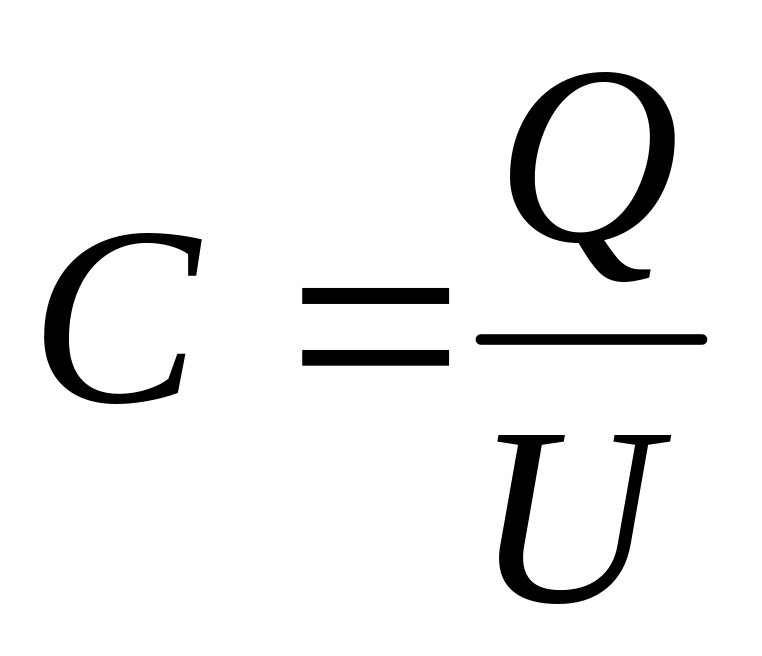(13.5)

где U=₁-₂ – разность потенциалов между его обкладками (или напряжение). Найдём выражение для электроёмкости наиболее распространённых типов конденсаторов.