1.2.6. Квадратурная модуляция

Квадратурная модуляция (англ.: QAM – Quadrature Amplitude Modulation) – разновидность амплитудной модуляции сигнала, которая позволяет модулировать несущую частоту одновременно двумя сигналами путем модуляции амплитуды несущей одним сигналом, и фазы несущей другим сигналом. Уравнение результирующих колебаний амплитудно-фазовой модуляции:

е(t) = u(t) cos(ω_ot+(t)).

Сигнал е(t) обычно формируют в несколько другой последовательности, с учетом последующей демодуляции. Раскроем косинус суммы и представим сигнал в виде суммы двух АМ-колебаний.

е(t) = u(t) cosω_ot·cos(t) – u(t) sinω_ot·sin(t).

При a(t) = u(t) cos(t) и b(t) = –u(t) sin(t), сигналы a(t) и b(t) могут быть использованы в качестве модулирующих сигналов несущих колебаний cosω_ot и sinω_ot, сдвинутых по фазе на 90^о относительно друг друга:

е(t) = a(t) cosω_ot + b(t) sinω_ot.

Полученный сигнал называют квадратурным (quadrature), а способ модуляции – квадратурной модуляцией (КАМ) (рис. 11).

Рис. 11. Квадратурная модуляция

Спектр квадратурного сигнала может быть получен непосредственно по уравнению балансной модуляции (10) для суммы двух сигналов:

S(ω) = ½ A(ω+ω_o) + ½ A(ω-ω_o) – ½j B(ω+ω_o) + ½j B(ω-ω_o).

Демодуляция квадратурного сигнала соответственно выполняется умножением на два опорных колебания, сдвинутых относительно друг друга на 90^о:

е₁(t) = е(t) cosω_ot = ½ a(t) + ½ a(t) cos2ω_ot + ½ b(t) sin2ω_ot,

е₂(t) = е(t) sinω_ot = ½ b(t) + ½ a(t) sin2ω_ot - ½ b(t) cos2ω_ot.

Низкочастотные составляющие a(t) и b(t) выделяются фильтром низких частот. Как и при балансной амплитудной модуляции, для точной демодуляции сигналов требуется точное соблюдение частоты и начальной фазы опорного колебания.

Квадратурная модуляция применяется для передачи сигналов цветности в телевизионном стандарте PAL и NTSC, в стереофоническом радиовещании.

1.3. Угловая модуляция

При угловой модуляции (angle modulation) в несущем гармоническом колебании u(t)=U_нcos(t+) значение амплитуды колебаний U_н остается постоянным, а информация е(t) переносится либо на частоту , либо на фазовый угол . И в том, и в другом случае текущее значение фазового угла гармонического колебания u(t) определяет аргумент (t) = t+, который называют полной фазой колебания.

1.3.1. Фазовая модуляция

Фазовая модуляция (ФМ, phase modulation – PM) – один из видов модуляции колебаний, при которой информационный сигнал управляет фазой несущего колебания. При фазовой модуляции значение фазового угла ₀ постоянной несущей частоты колебаний _o пропорционально амплитуде модулирующего сигнала е(t), т.е. ₀ = е(t). Соответственно, уравнение ФМ – сигнала определяется выражением:

u(t) = U_н cos[_ot + kе(t)+j₀], (15)

где k – коэффициент пропорциональности, который называется индексом фазовой модуляции.

Пример однотонального ФМ – сигнала приведен на рис. 12.

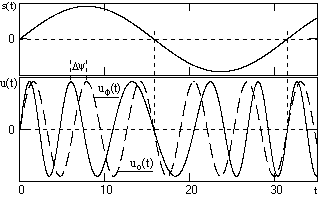
Рис. 12. Фазомодулированный сигнал

При е(t) = 0, ФМ-сигнал является простым гармоническим колебанием и показан на рисунке функцией u_o(t). С увеличением значений е(t) полная фаза колебаний:

(t)=_ot+kе(t)+j_0,

нарастает во времени быстрее и опережает линейное нарастание _ot. Соответственно, при уменьшении значений е(t) скорость роста полной фазы во времени спадает. В моменты экстремальных значений е(t) абсолютное значение фазового сдвига  между ФМ – сигналом и значением _ot немодулированного колебания также является максимальным и носит название девиации фазы (вверх _в = kе_max(t)+j₀, или вниз _н = kе_min(t)+j₀ с учетом знака экстремальных значений модулирующего сигнала).

Для колебаний с угловой модуляцией применяется также понятие мгновенной частоты (instantaneous frequency), под которой понимают производную от полной фазы по времени:

ω(t) = (t)/dt = ω_o + k dе(t)/dt.

Полная фаза колебаний в произвольный момент времени может быть определена интегрированием мгновенной частоты:

(t) = ω(t)dt, или (t) = ω(t)dt+_o.

Фазовая модуляция, не связанная с начальной фазой несущего сигнала, называется относительной фазовой модуляцией (ОФМ).

При относительной фазовой модуляции (ОФМ, DPSK – Differential Phase Shift Keying) в зависимости от значения информационного элемента изменяется только фаза сигнала при неизменной амплитуде и частоте. Причем каждому информационному биту ставится в соответствие не абсолютное значение фазы, а ее изменение относительно предыдущего значения. Чаще применяется четырехфазная ОФМ (ОФМ-4), или двукратная ОФМ (ДОФМ), основанная на передаче четырех сигналов, каждый из которых несет информацию о двух битах (дибите) исходной двоичной последовательности. Обычно используется два набора фаз: в зависимости от значения дибита (00, 01, 10 или 11) фаза сигнала может измениться на 0°, 90°, 180°, 270° или 45°, 135°, 225°, 315° соответственно. При этом, если число кодируемых бит более трех (8 позиций поворота фазы), резко снижается помехоустойчивость ОФМ. По этой причине для высокоскоростной передачи данных ОФМ не используется.

В случае, когда информационный сигнал является дискретным, то говорят о фазовой манипуляции. Хотя, строго говоря, в реальных изделиях манипуляции не бывает, так как для сокращения занимаемой полосы частот манипуляция производится не прямоугольным импульсом, а колоколообразным. Несмотря на это, при модуляции дискретным сигналом говорят только о манипуляции.

По характеристикам фазовая модуляция близка к частотной модуляции. В случае синусоидального модулирующего (информационного) сигнала, результаты частотной и фазовой модуляции совпадают.