Решение

1. Дополним табл. 1 столбцами, необходимыми для расчета оценок параметров множественной линейной регрессии, и строками для расчета сумм и средних значений по столбцам.

Рассчитаем суммы и средние значения по каждому столбцу. Найдём выборочные дисперсии для факторов . Результаты расчетов представлены на рис. 1.

Рис. 1. Результаты расчетов сумм, средних значений и дисперсий

Составим определитель системы нормальных уравнений (2) и определители при неизвестных коэффициентах . Вычислим определители, используя функцию МОПРЕД из категории Математические. Найдём коэффициенты уравнения, используя формулы Крамера (3). Полученные значения коэффициентов приведены на рис. 2.

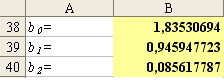
Рис. 2. Результаты расчетов коэффициентов уравнения регрессии

Проверим расчеты, используя формулу (4). Для этого составим матрицы и так, как показано в методических указаниях к теме. Вычисление матрицы будем производить поэтапно. Сначала вычислим матрицу , используя встроенную функцию ТРАНСП из категории Ссылки и массивы (для транспонирования матрицы) и МУМНОЖ из категории Математические (для умножения матриц). Выделим диапазон ячеек, в котором будет выведен результат вычислений (для условия примера диапазон имеет размер ). Нажмем клавишу «F2». В первую ячейку для искомой матрицы вызовем функцию МУМНОЖ. В поле Массив 1 введем от руки имя функции ТРАНСП и в скобках укажем диапазон ячеек, содержащий матрицу , в поле Массив 2 введем диапазон ячеек, содержащий матрицу (рис. 3).

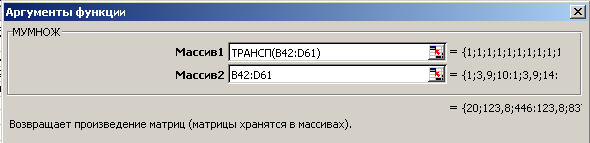
Рис. 3. Заполнение полей аргументов функции МУМНОЖ

Еще раз нажмем клавишу «F2» (при этом аргументы функции подсветятся) и затем нажмем одновременно клавиши «Ctrl» + «Shift» + «Enter». Excel поместит рассчитанную матрицу во все выделенные ячейки и автоматически заключит формулы в фигурные скобки, чтобы подчеркнуть, что это формулы массива. (Вручную их вводить нельзя, это будет ошибкой). Результаты расчетов представлены на рис. 4.

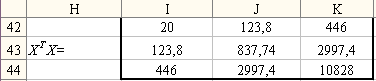
Рис. 4. Результаты расчета матрицы Х^ТХ

Для нахождения обратной матрицы используем функцию МОБР из категории Математические. Выделим диапазон ячеек, в котором будет выведен результат вычислений (для условия примера диапазон имеет размер ). Нажмем клавишу «F2». В первую ячейку для искомой матрицы вызовем функцию МОБР. В поле Массив введем диапазон ячеек, содержащий матрицу (рис. 5).

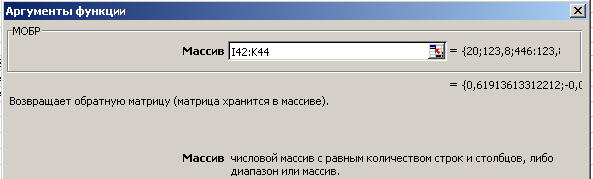
Рис. 5. Заполнение полей аргумента функции МОБР

Еще раз нажмем клавишу «F2» (при этом аргумент функции подсветится) и затем нажмем одновременно клавиши «Ctrl» + «Shift» + «Enter». В результате получим обратную матрицу (Х^ТХ)^-1:

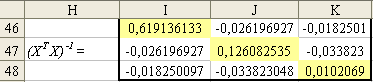
Рис. 6. Результаты расчета матрицы (Х^ТХ)^-1

Аналогично вычислению матрицы найдем матрицу (она будет иметь размер ):

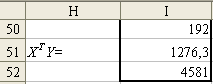
Рис. 7. Результаты расчета матрицы

Перемножив матрицы и , получим матрицу . Результаты расчетов коэффициентов совпадают.

Вывод: модель зависимости выработки продукции на одного работника от ввода в действие новых основных фондов и удельного веса рабочих высокой квалификации имеет вид: . При увеличении ввода в действие новых основных фондов (при неизменном ) на 1% выработка продукции повысится в среднем на 0,9459 млн. руб., а при увеличении удельного веса рабочих высокой квалификации (при неизменном ) на 1% выработка повысится в среднем на 0,856 млн. руб.

2. Рассчитаем средние коэффициенты эластичности по формуле (5) (рис. 8).

Рис. 8. Результаты расчета средних коэффициентов эластичности

Вывод: при увеличении ввода в действие новых основных фондов (при неизменном ) на 1% выработка продукции повысится в среднем на 0,61%, а при увеличении удельного веса рабочих высокой квалификации (при неизменном ) на 1% выработка повысится в среднем на 0,20%. Таким образом, подтверждается бóльшее влияние на результат фактора , чем фактора .

3. Определим коэффициент множественной детерминации. Для этого дополним табл. 1 столбцами для расчета значений и квадратов отклонений . Заполним столбцы (рис. 9).

Рис. 9. Результаты расчета и квадратов отклонений

Вычислим коэффициент множественной детерминации R² по формуле (6), коэффициент множественной корреляции R = и скорректированный коэффициент множественной детерминации Ř² по формуле (8). Результаты вычислений приведены на рис. 10.

Рис. 10. Результаты расчета коэффициентов

Вывод: значение R² = 0,9469 указывает на весьма высокую степень обусловленности изменения результата изменением факторов.

Значение R = 0,973 указывает на тесную связь между результативным и факторными признаками.

Значение Ř² = 0,9407 также указывает на высокую детерминированность результата y в модели факторами и .

Для проверки значимости уравнения в целом найдем фактическое значение критерия Фишера по формуле (9).

Для нахождения критического значения распределения Фишера используем Статистическую функцию FРАСПОБР, заполнение полей которой показано на рис. 11.

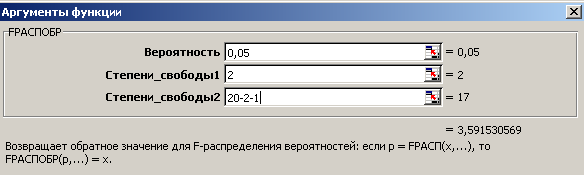
Рис. 11. Заполнение полей аргументов функции FРАСПОБР

Для сравнения фактического и критического значений используем Логическую функцию ЕСЛИ, заполнение полей которой приведено на рис. 12.

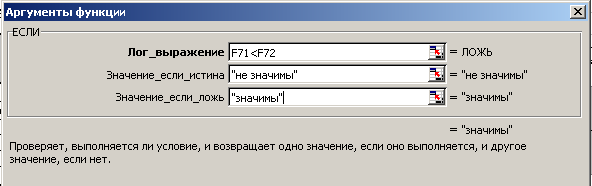
Рис. 12. Заполнение полей аргументов функции ЕСЛИ

Результаты расчетов приведены на рис. 13.

Рис. 13. Результаты проверки значимости уравнения

Вывод: уравнение регрессии и коэффициент детерминации R² статистически значимы.

4. Определим выборочную остаточную дисперсию S² по формуле (10). Стандартную ошибку регрессии высчитаем как квадратный корень из остаточной дисперсии . Стандартные ошибки коэффициентов регрессии найдем, используя матрицу , рассчитанную в пункте 1. Рассчитаем наблюдаемые (фактические) значения t-статистик по формулам (12). Для нахождения критического значения распределения Стьюдента используем Статистическую функцию СТЬЮДРАСПОБР, заполнение полей которой представлено на рис. 14.

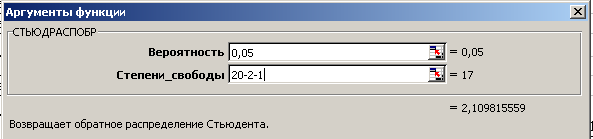
Рис. 14. Заполнение полей аргументов функции СТЬЮДРАСПОБР

Для сравнения наблюдаемого и критического значений критерия используем Логическую функцию ЕСЛИ.

Результаты расчетов показаны на рис. 15.

Рис. 15. Проверка значимости коэффициентов

Вывод: статистически значимыми являются коэффициенты . Фактор , силу влияния которого оценивает коэффициент b₂, можно исключить как несущественно влияющий.

5. Матрицу парных коэффициентов корреляции рассчитаем, используя инструмент «Корреляция» из раздела «Анализ данных».

В главном меню выберем Сервис/ Анализ данных/ Корреляция, после чего щелкнем по кнопке ОК. В появившемся окне заполним поля ввода данных и параметров вывода диалогового окна (рис. 16).

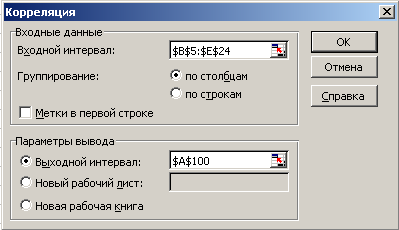
Рис. 16. Диалоговое окно ввода параметров инструмента «Корреляция»

Входной интервал – диапазон, содержащий данные результирующего признака и факторных признаков.

Метки в первой строке – флажок, который указывает, содержит ли первая строка названия столбцов.

Выходной интервал – укажем левую верхнюю ячейку диапазона ячеек для вывода результата.

Введем наименования столбцов и дополним матрицу, используя ее симметричность. Результат представлен на рис. 17 (матрица межфакторных коэффициентов корреляции выделена двойной рамкой).

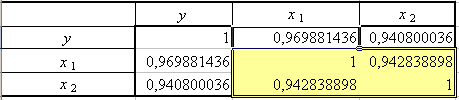
Рис. 17. Матрица коэффициентов парной корреляции

Вывод: значения коэффициентов парной корреляции указывают на весьма тесную связь выработки y как с коэффициентом обновления основных фондов x₁, так и с долей рабочих высокой квалификации x₂ ( ). Межфакторная связь весьма тесная и превышает тесноту связи x₂ с y, то есть имеет место мультиколлинеарность факторов. Для улучшения данной модели можно исключить из нее фактор x₂ как статистически ненадежный.

Найдем – определитель матрицы коэффициентов межфакторной корреляции по формуле (15), используя функцию МОПРЕД. Найдем линейный коэффициент множественной корреляции R по формуле (13) (рис. 18).

Рис. 18. Результаты расчета определителя матрицы межфакторной корреляции

Вывод: значение определителя, равное 0,1111, говорит о мультиколлинеарности факторов.

6. Найдем частные коэффициенты корреляции по формулам (18) (рис. 19).

Рис. 19. Результаты расчета частных коэффициентов корреляции

Вывод: наиболее тесно связаны переменные и , связь между переменными и слабее. Необходимо исключить фактор из правой части уравнения множественной регрессии.

С помощью частных -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после фактора и фактора после .

Фактические значения критериев найдём по формулам (19). Для нахождения критического значения распределения Фишера используем Статистическую функцию FРАСПОБР, заполнение полей которой представлено на рис. 20.

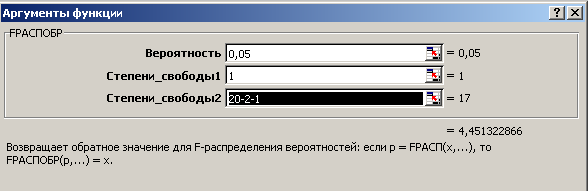
Рис. 20. Заполнение полей аргументов функции FРАСПОБР для частных - критериев

Для сравнения экспериментального и критического значений используем Логическую функцию ЕСЛИ, заполнение полей которой показано на рис. 21.

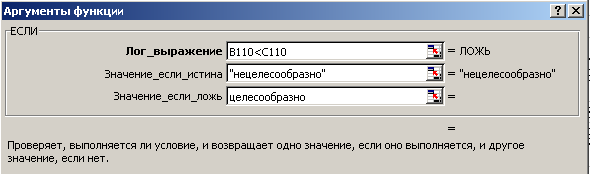
Рис. 21. Заполнение полей аргументов функции ЕСЛИ для частных - критериев

Получим результаты, представленные на рис. 22.

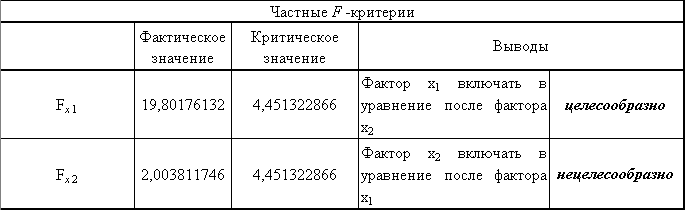
Рис. 22. Результаты применения частных - критериев

Вывод: включение в модель фактора х₂ (доля высококвалифицированных рабочих) после того, как в уравнение включен фактор х₁ (коэффициент обновления основных фондов), статистически нецелесообразно. Фактор х₁ должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора х₂.

7. Для проверки результатов расчетов в главном меню выберем Сервис/ Анализ данных / Регрессия, после чего щелкнем по кнопке ОК. Заполним поля ввода данных и параметров вывода диалогового окна (рис. 23).

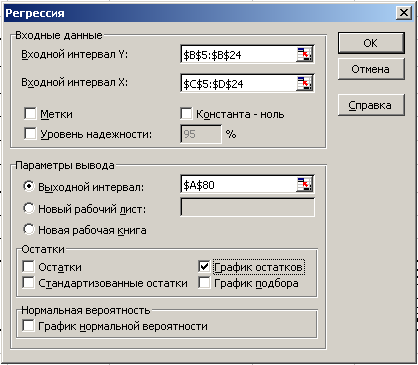
Рис. 23. Заполнение полей диалогового окна инструмента «Регрессия»

Входной интервал Y – диапазон, содержащий данные результативного признака.

Входной интервал X – диапазон, содержащий данные факторных признаков.

Метки – флажок, который указывает, содержит ли первая строка названия столбцов.

Константа–ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении.

Выходной интервал – укажем левую верхнюю ячейку диапазона ячеек для вывода результата.

Поставим флажок в поле График остатков.

Вывод: результаты вычислений пошагово и с помощью инструмента «Регрессия» совпадают (для наглядности в «Образце решения» результаты выделены одинаковым цветом).

8. Остатки на графиках и для х₁ и для х₂ попадают в горизонтальную полосу. Можно высказать предположение, что они не зависят от значений , то есть дисперсия остатков гомоскедастична. Проверим эту гипотезу по критерию Гольдфелда – Квандта для фактора х₁.

1. Упорядочим все наблюдения по возрастанию переменной х₁. Для этого скопируем табл. 1, вставим ее на свободное место листа и выделим числовые значения. В главном меню выберем Данные / Сортировка. Заполним поля ввода данных и параметров вывода диалогового окна Сортировка диапазона. В поле Сортировать по укажем столбец, содержащий значения переменной х₁. В поле Параметры отметим, что следует сортировать строки диапазона (рис. 24).

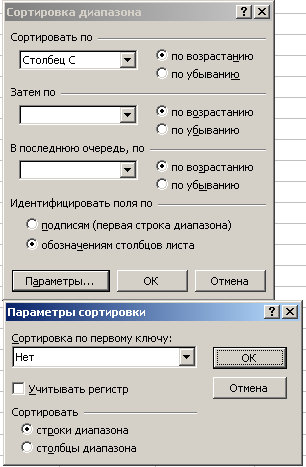
Рис. 24. Заполнение полей диалогового окна инструмента «Сортировка»

В результате получим таблицу:

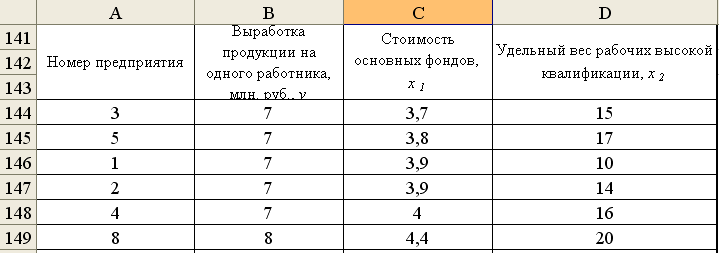
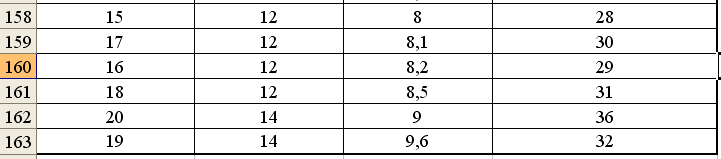
Рис. 25. Результат сортировки

2. Оценим отдельно регрессии, используя инструмент Регрессия, для первых n₀ = 6 и для последних n₀ = 6 наблюдений. Средние наблюдений отбросим. В таблицах дисперсионного анализа для первых и последних 6 наблюдений выделим суммы квадратов остатков (рис. 26 и 27).

Рис. 26. Дисперсионный анализ для первых шести наблюдений

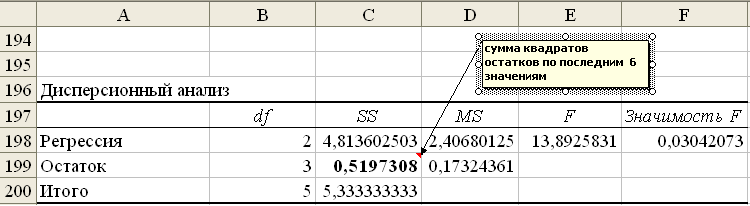
Рис. 27. Дисперсионный анализ для последних шести наблюдений

3. Вычислим статистику Фишера:

,

Для нахождения критического значения распределения Фишера F_кр = = F (0,05; ν₁ = ν₂ = 6 – 2 – 1) используем Статистическую функцию FРАСПОБР, для сравнения экспериментального и критического значений используем Логическую функцию ЕСЛИ (рис. 28).

Рис. 28. Результат проверки

Вывод: в модели отсутствует гетероскедастичность, зависящая от переменной x₁.

 