2. . Практическое задание

По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (млн. руб.) от ввода в действие новых основных фондов х₁ (процент от стоимости фондов на конец года) и удельного веса рабочих высокой квалификации в общей численности рабочих х₂ (%). Данные по вариантам приведены в папке Эконометрика \ Задание 2.

Требуется:

1. Оценить параметры линейного уравнения множественной регрессии, решив систему нормальных уравнений по формулам Крамера и с использованием матричного умножения, пояснить экономический смысл его параметров.

2. Дать сравнительную оценку силы связи результативного признака и факторных признаков с помощью средних коэффициентов эластичности.

3. Оценить качество модели, вычислив коэффициенты множественной детерминации, корреляции и скорректированный коэффициент множественной детерминации. Проверить значимость уравнения в целом с помощью критерия Фишера при уровне значимости α = 0,01. Сделать выводы.

4. Оценить статистическую значимость оценок параметров регрессионной модели с помощью критерия Стьюдента при уровне значимости α = 0,01.

5. Установить, имеет ли место коллинеарность факторов с использованием матрицы парных и межфакторных коэффициентов корреляции. Рассчитать коэффициент множественной корреляции. Сравнить найденное значение со значением, вычисленным в пункте 3.

6. С помощью частных 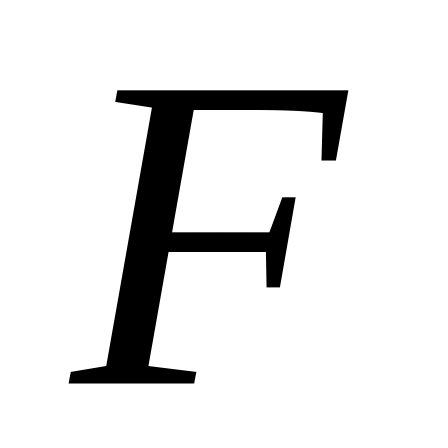-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора 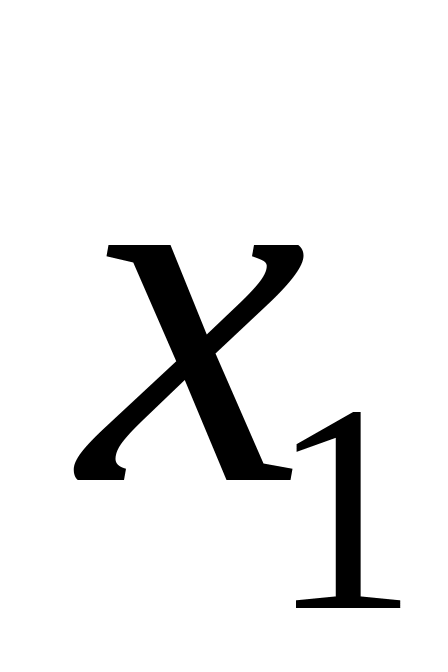после фактора 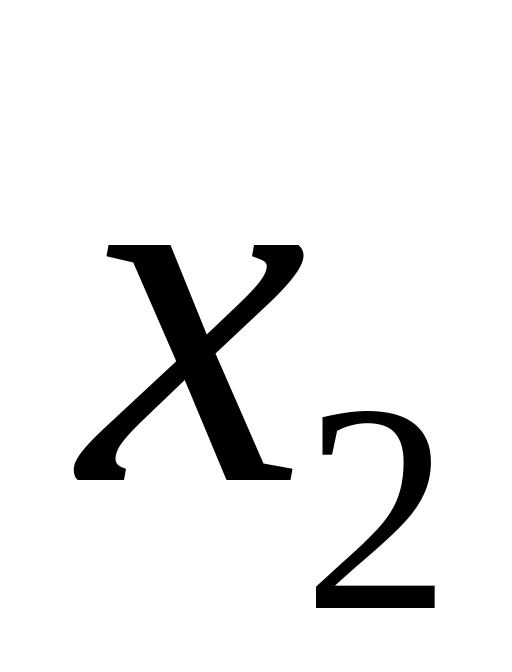и фактора после .

7. Проверить результаты расчетов с помощью инструмента «Регрессия» из раздела «Анализ данных». Построить графики остатков.

8. По графикам остатков выдвинуть гипотезу о наличии или отсутствии гетероскедастичности. Провести тестирование на гетероскедастичность, применив тест Гольфелда – Квандта.

Указание

Следует скопировать в созданную папку ФИО_Эконометрика рабочую книгу в соответствии с вариантом из папки Эконометрика \ Задание 2 и выполнять решение задания.

2.3. Решение типового задания

Пример. По 20 предприятиям региона (табл. 2) изучается зависимость выработки продукции на одного работника y (млн. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х₂ (%).

Таблица 2

Номер предприятия
1	7	3,9	10
2	7	3,9	14
3	7	3,7	15
4	7	4	16
5	7	3,8	17
6	7	4,8	19
7	8	5,4	19
8	8	4,4	20
9	8	5,3	20
10	10	6,8	20
11	9	6	21
12	11	6,4	22
13	9	6,8	22
Окончание табл. 2
Номер предприятия
14	11	7,2	25
15	12	8	28
16	12	8,2	29
17	12	8,1	30
18	12	8,5	31
19	14	9,6	32
20	14	9	36

Требуется:

1. Оценить параметры линейного уравнения множественной регрессии фактора y и факторов 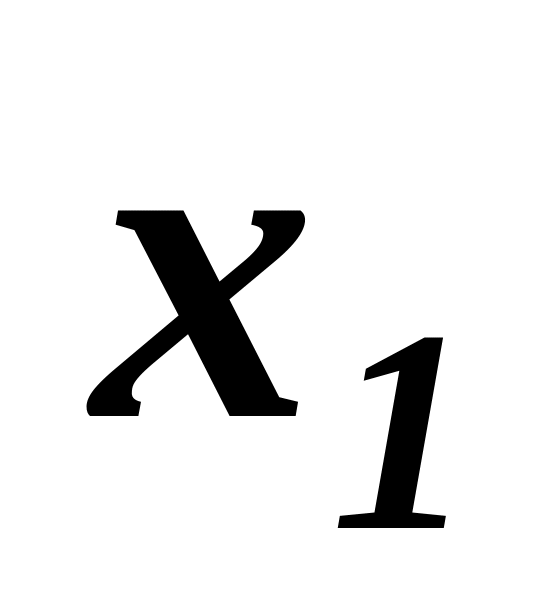и 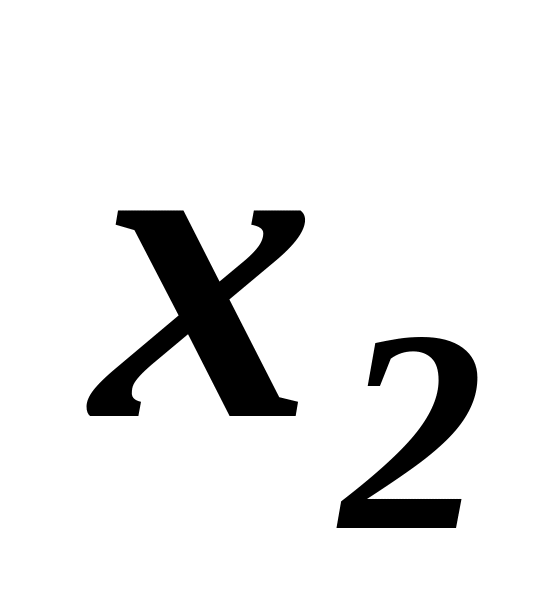, решив систему нормальных уравнений по формулам Крамера и с использованием матричного умножения, пояснить экономический смысл его параметров.

2. Дать сравнительную оценку силы связи результативного фактора y и факторов и с помощью средних коэффициентов эластичности.

3. Определить коэффициент множественной детерминации и корреляции. Рассчитать скорректированный коэффициент множественной детерминации. Проверить значимость уравнения в целом с помощью F-кри-терия Фишера при уровне значимости 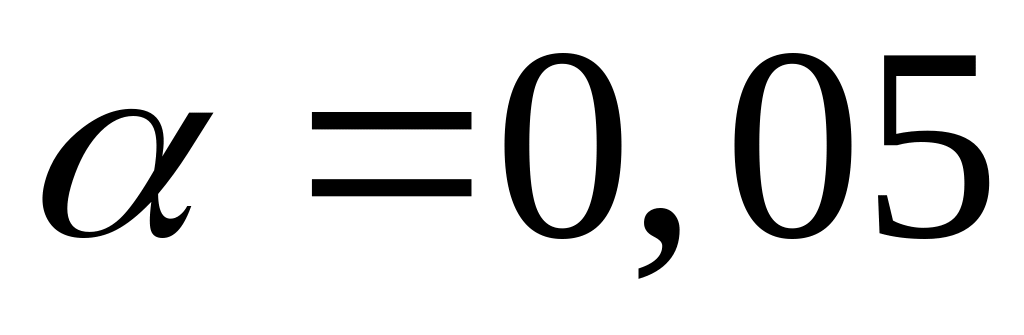. Сделать выводы.

4. Найти стандартную ошибку уравнения регрессии и стандартные ошибки коэффициентов регрессии. Оценить статистическую значимость оценок параметров регрессионной модели с помощью критерия Стьюдента при уровне значимости .

5. Рассчитать матрицы парных и межфакторных коэффициентов корреляции. Установить, имеет ли место коллинеарность факторов. Рассчитать коэффициент множественной корреляции. Сравнить найденное значение со значением, вычисленным в пункте 3.

6. Найти частные коэффициенты корреляции. С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после фактора и фактора после .

7. Проверить результаты расчетов с помощью инструмента «Регрессия» из раздела «Анализ данных». Построить графики остатков.

8. По графикам остатков высказать гипотезу о наличии или отсутствии гетероскедастичности. Провести тестирование уравнения множественной регрессии на гетероскедастичность, применив тест Гольфелда – Квандта.